Here is an interesting little question. Its answer is simple, and not hard to see just by graphing examples; yet the algebra is easy to get wrong, as we’ll see several times. And subtle errors deserve study.
Where do xn and x1/n intersect?
The question came from Amia in late April:
Hi Dr Math,
Can you help me to solve this question:
Find the intersection points for the two functions f(x) = xn , g(x) = x1/n, n a positive integer.
One thing that makes this interesting is that we want a general answer for any n, not just a solution of a single equation; the behavior of these functions varies with n.
Looking at the graphs
Doctor Rick answered:
Yes, we will be glad to help you. As you know from working with us, our focus is on helping you solve the problem, which means we need to see your ideas or thoughts first in order to proceed.
Sketching a few graphs should give you a good idea of the solution. Try sketching the graphs for n = 1, 2, 3, and 4. Then tell us what you observe, what conclusions you draw, and what questions remain in your mind.
Sketching will take a little thought if you do it by hand (which is worth the trouble!). But I’ve made the graphs he suggests the easy way, using Desmos:
For \(n=1\): \(f(x)=x^1=x, g(x)=x^{1/1}=x\)
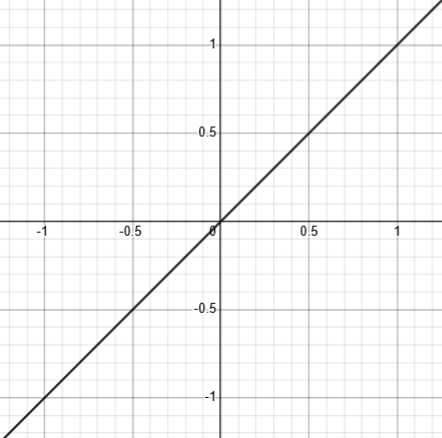
(Here, black represents the solution: Since the two functions are identical, every point on the line is a solution!)
For \(n=2\): \(f(x)=x^2, g(x)=x^{1/2}=\sqrt[2]{x}\)
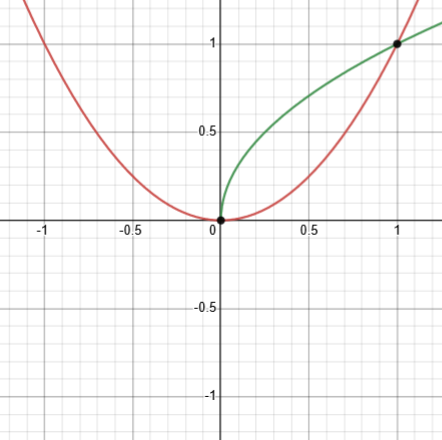
Here, there are only two solutions, 0 and 1.
For \(n=3\): \(f(x)=x^3, g(x)=x^{1/3}=\sqrt[3]{x}\)
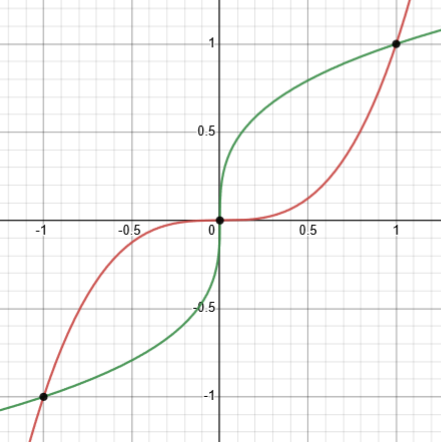
Now there are three solutions: \(-1,0,1\).
For \(n=4\): \(f(x)=x^4, g(x)=x^{1/4}=\sqrt[4]{x}\)
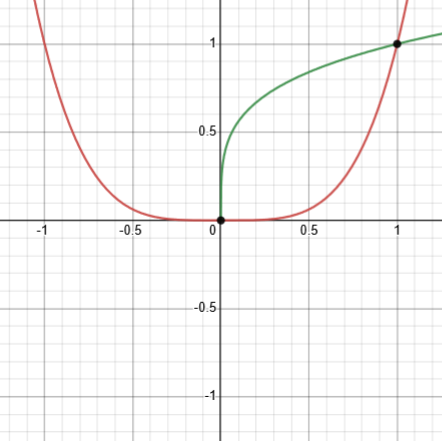
Now we’re back to only two solutions.
There is a clear pattern: For odd n greater than 1, there are three solutions (\(-1, 0, 1\)), while for even n greater than 0, there are only two solutions (\(0, 1\)). But graphs don’t prove anything, so we want more.
Trying algebra
Amia replied, giving an answer, then the algebraic reasoning (rather than making graphs):
When n is odd x = 0, -1, 1
When n is even x = 0, 1
I start with equaling f and g,
xn = x1/n
By raising the two sides to the power n:
(xn)n = x
x(1 – (xn)n-1) = 0
x = 0 , (xn)n-1 = 1
If n is odd, x = 1. If n is even, x = -1, 1.
The last line must have a typo (since it doesn’t match the answer given), and the work itself isn’t quite right either. We’ll correct it at the end; for now, see if you can identify the error for yourself. (It’s easy to miss, especially when you are following someone else’s work whom you generally trust; neither Doctor Rick nor I caught this one until I was editing it just now!)
Doctor Rick replied, first commenting on the answer given in the first two lines, and then on the work:
Yes, that’s the solution I find by extrapolating from what I see in my sketches for n = 2 and 3. It’s not quite complete.
I am hesitant to raise both sides to the power n, because I know this can introduce extraneous roots. It’s fine for odd n, since f(x) = xn is a monotonically increasing function for odd integers n; but I’d want to handle even values of n separately if I took this approach.
I don’t know how you reached your conclusion from the line above it. What I see there is that
x = 0 OR xn(n–1) = 1
In the second case, the exponent is necessarily even (since either n or n–1 must be even), so I conclude x = 1 or –1 … for any n, odd or even. But an extraneous root has indeed been introduced for even n.
The sort of extraneous roots mentioned here is the second one discussed in Extraneous Solutions: Causes and Cures. For an odd exponent, \(f(x)=x^n\) is monotonically increasing, meaning that whenever x increases, so does y; as a result, it is one-to-one and the result of applying it to an equation is equivalent to the original equation. But for an even exponent, the function is not one-to-one, so that the new equation may be true when the original was not.
Amia’s big error is in factoring \(\left(x^n\right)^n\) as \(x\cdot\left(x^n\right)^{n-1}\), when the former would really be equivalent to \({\color{Red}{x^n}}\cdot\left(x^n\right)^{n-1}\), Doctor Rick either missed, or chose not to point out, that error in the work leading to the line he quoted.
My own thought was to start as you did, but divide both sides by x1/n:
xn = x1/n [1]
xn / x1/n = 1
xn – 1/n = 1 [2]
Being careful not to gain or lose solutions, I must note that what I did above is not allowed if x1/n = 0, which will happen if and only if x = 0. Thus I must consider that case separately, and I see that x = 0 satisfies the original equation for any n.
So we have found that \(x=0\) is a solution for all n; what else?
Continuing with the x ≠ 0 case, my thought was to write 1 as x0, and use a property of exponents to conclude that
n – 1/n = 0
But here x has vanished, and I find the solution n = ±1. Since n is restricted to positive integers, I seem to have proved that
(a) x = 0 is a solution of [1] for all positive integers n.
(b) Any real x is a solution of [1] if n = 1.
And that’s all! Whereas your approach (as I interpreted it) introduced spurious solutions, my method has missed solutions. What did I do wrong?
I know where the error lies. Can you see it? It has to do with the conditions on the property of exponents that I used.
Making a mistake can be a teaching opportunity; learning to recognize (subtle) errors is important. So, what did he do wrong?
(Notice that we have found the case Amia missed, namely that all real x are solutions when \(n=1\); but we haven’t yet found that \(x=1,-1\) are solutions.)
Checking the conditions
After Amia replied, unable to locate the error, Doctor Rick added a hint:
Did you notice the property of exponents that I used? I didn’t state it explicitly, but it was this:
If xa = xb then a = b.
Under what conditions on the variables is this true?
Whenever we apply a property, we need to make sure it applies under that conditions that are present.
Amia made an unclear reply, to which Doctor Rick answered:
What I asked you was: Under what conditions on the variables is it true that
If xa = xb then a = b ?
I have looked for a full statement of this property, but many lists of properties of exponents only include those that are useful in simplifying exponential expressions. Here is one place online that I find the full statement:
https://www.varsitytutors.com/hotmath/hotmath_help/topics/solving-exponential-equations
If b is a positive number other than 1, then bx = by if and only if x = y .
Thus we can’t apply the property if the base (x for us) is negative, 0, or 1.
This property is the one-to-one property of exponentiation: It says that there is only one exponent (with a given base, which in our context is x) that will produce any given number (if any). It is not true if the base is 0 (since zero to any (non-zero) power is 0), or if the base is 1 (since 1 to any power is 1), or if the base is negative (we’ll explore this below).
I find an equivalent statement in a textbook:

Other sources may be more vague because they hide the conditions on the base inside their definition of what counts as an exponential function. It’s easy to forget, as he said, because we normally work only with proper exponential functions.
I applied the property with a = n – 1/n and b = 0 (or equivalently, with a = n and b = 1/n). I concluded that n must be 1 or –1. In those cases x could have any value; otherwise there was no solution. But now we see that this conclusion applies only to x > 0, x ≠1. Thus here is what I have established so far:
Solve
xn = x1/n [1]
where n is a positive integer.
If n = 1, we have x1 = x1 and every x is a solution. (This is the part you have missed.)
Otherwise, no positive x other than 1 could be a solution.
Checking x = 0 and x = 1, we find that both are solutions for any n.
We saw that missing case in our first graph above. Special cases are easy to miss when you are doing algebra, because we get used to assuming that variables have typical values, not exceptional values!
What about negatives?
We still haven’t settled the question of negative x. The trouble with negative bases is that a non-integer power of a negative number is in general complex (and not single-valued). But here, we know xn is real, so for any solution, x1/n must be real. For negative x, this will only be the case if n is odd. This establishes that, for even n (except 0), the only two solutions of equation [1] are 0 and 1.
For even n, \(x^{1/n}=\sqrt[n]{x}\) will be undefined (as far as a graph is concerned) for negative x; for example, \((-4)^{1/2}=\sqrt[2]{-4}=2i\), which is not a real number, and so can’t be graphed. That is, the domain of this function is restricted to non-negative real numbers. So we can ignore the negative case for even n; we’ve already found all solutions.
But whereas raising both sides of an equation to an even power yields extraneous roots, an odd power is well behaved, with its domain including all real numbers:
For odd n, we can do as you did — because, as I said earlier, f(x) = xn is a monotonically increasing function if n is odd. We raise both sides of equation [1] to the nth power, obtaining
(xn)n = (x1/n)n
x2n = x
x2n – x = 0
x(x2n–1 – 1) = 0
x = 0 or x2n–1 = 1
Since 2n–1 is odd, in the second case x is a real odd root of unity, namely 1 or –1.
This is all rather ugly, compared to simply sketching graphs, which gave us the solution quickly and cleanly.
Unfortunately, Doctor Rick has made a mistake similar to Amia’s: \((x^n)^n\) is not \(x^{n+n}=x^{2n}\), but \(x^{n\cdot n}=x^{n^2}\), just as \(\left(x^\frac{1}{n}\right)^n=x^{n\cdot\frac{1}{n}}=x^1=x\). So the work here should be $$(x^n)^n=\left(x^\frac{1}{n}\right)^n\\x^{n^2}=x\\x^{n^2}-x=0\\x\left(x^{n^2-1}-1\right)=0\\x\left(x^{(n+1)(n-1)}-1\right)=0$$ So either \(x=0\) or \(x^{(n+1)(n-1)}=1\). Since we are assuming n is odd, the exponent is even, And there are two even roots of \(1\), namely \(1\) and \(-1\). (The only real odd root of unity is unity.)
So we can conclude that for even n, the solutions are \(0,1\), and for odd n, the solutions are \(-1,0,1\); while for \(n=1\), all x are solutions. This is what we saw in the graphs.
That may feel like more work than we needed; but it’s good exercise.
For a question with interesting relationships with this one, see When Can a Function Equal Its Inverse?
