A recent question from a student demonstrates that not everything on the Internet should be taken at face value – and that it’s easy to think you are right when you are not.
Here is the question, from late April, with two parts:
I have seen a statement – All polynomial functions of odd order have at least one zero, while polynomial functions of even order may not have a zero. what does this statement mean? What is the relation between order of polynomial and no. of real zeroes in a polynomial?
I have seen a formula in a YouTube video which I have not seen in any textbook and the formula is
No. of turning points in a polynomial graph = no. of zeros + 1 – no. of even zeros.
Is this formula correct?
I know that maximum no of turning points possible for a polynomial of degree n is (n-1) and this is self-evident. But how the above formula comes? Plz help.
The order (or degree) of a polynomial is the greatest exponent on the variable. A zero of a function is an input for which the function’s value is zero; on a graph, a real zero is an x-intercept. A turning point on a graph is a point where it changes from increasing to decreasing, or vice versa.
How many real zeros?
Doctor Rick answered, first dealing with the first paragraph:
Hi, Debarghya.
The number of real zeros of a polynomial is less than or equal to the degree (order) of the polynomial. For instance, f(x) = x2 – 1 (order 2) has two real zeros; g(x) = x2 has one zero (of multiplicity 2); and h(x) = x2 + 1 has no real zeros.
Note that Debarghya is talking about graphs, and therefore ignoring non-real zeros, which are not visible on a (real-valued) graph. That will eventually become an issue!
Here are the graphs of those three functions (f, g, h), showing how you can get 2, 1, or 0 (real) zeros:
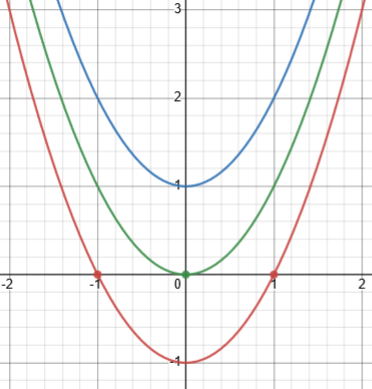
These all have one turning point. You can see how an even degree makes it possible to have no (real) zeros.
There are (at least) two good ways to understand why polynomials of odd degree have at least one zero, depending on what you have learned about polynomials.
One way is to think about the graph of a polynomial P(x). As x gets far from zero, the behavior of the graph is dominated by the leading term. If the leading coefficient is positive, then xn will increase without limit as x increases, and hence P(x) > 0 for sufficiently great x. On the other hand, as x decreases (becomes increasingly negative), xn will approach negative infinity for odd n. Since a polynomial is a continuous function, its graph must cross the x axis somewhere, in order to change from negative to positive. Thus there must be at least one zero of the function (x-intercept of the graph).
If a continuous graph is below the x-axis at one end, and above the x-axis at the other, then it must cross at least once.
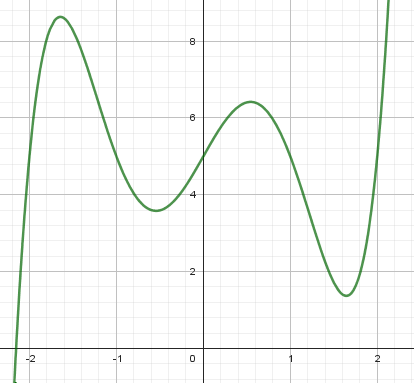
Here are two polynomials with degree 9, one crossing only once, the other more:
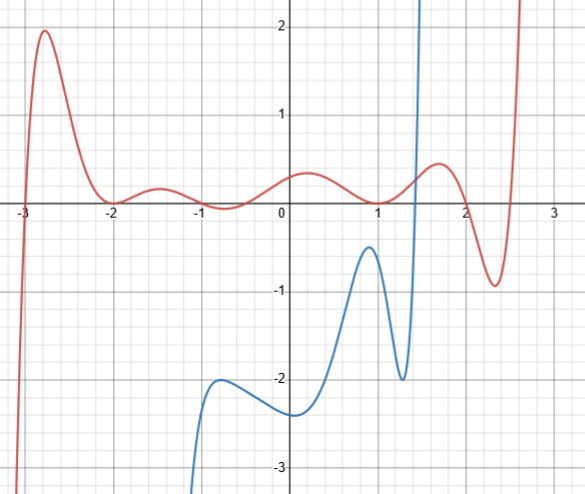
The red one has 7 zeros and 8 turning points (two of which are also zeros); the blue one has one zero and 4 turning points. Both illustrate the fact that the number of zeros is at most n, and the number of turning points is at most \(n-1\).
The other way is to use the Fundamental Theorem of Algebra: that every polynomial equation of degree n with complex number coefficients has n roots, or solutions, in the complex numbers. We’re talking, I assume, about real coefficients, in which case it is proved further that any non-real roots must come in complex-conjugate pairs, that is, if a+bi is a root then a-bi is also a root. From this we can see that the number of real roots (counting multiplicity) must have the same parity (odd or even) as the degree of the polynomial. Since zero is an even number, an odd-degree polynomial can’t have zero real roots — it must have at least one.
Equivalently, a polynomial with odd degree can be factored into an odd number of linear factors (corresponding to zeros); and any factors corresponding to non-real zeros must come in pairs, so that removing them leaves an odd number of factors representing real zeros. Therefore, there can’t be zero real zeros.
The Fundamental Theorem of Algebra implies that the number of zeros of a polynomial is no more than its degree; and when applied to the derivative (a concept from calculus) it implies that the number of turning points (which are zeros of the derivative) is no more than one less than the degree. So all these claims are easy to prove.
How many turning points?
Now, about the video and its formula:
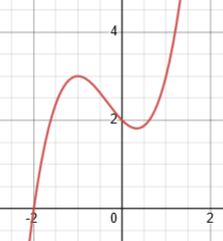
I don’t know what is meant by “even zeros” in that formula. My guess would be “zeros of even multiplicity“, but the formula is not valid with that meaning. For example, here is the graph of f(x) = (x – 2)(x – 1)x(x + 1)(x + 2) + 5; it has one zero, but four turning points.
Perhaps you could show us where you saw the formula.
This example has degree 5, with one (odd) zero and four turning points; it is not true that “No. of turning points = no. of zeros + 1 – no. of even zeros,” which would give \(T=Z+1-E=1+1-0=2\), rather than the correct answer, 4.
The source of the claim
While we waited for more information, I did some searching:
I found what I presume is the source video,
How to find number of turning points of polynomial using Formula from equations with 5 examples
Here is the final screenshot showing all his examples:
We see, first, that the formula was misstated above, with the wrong signs; but it is still not true for Doctor Rick’s example, taken at face value: \(Z-1+E=1-1+0=0\), which is not the number of turning points, 4.
But watching the video, we see that his numbers at the right are not quite what he says they are:
For examples b and c, which are like Doctor Rick’s example, he ignores the added constants! So he is not really counting zeros of the given polynomial, but zeros of a shifted polynomial that has a full number of real zeros. This makes his claim work (when interpreted as he does) for Doctor Rick’s example.
But he doesn’t even make an attempt to show that his results are true! That means this is not mathematics. (I think all his examples are correct, but they do not exhaust the possibilities.)
I don’t know exact conditions under which what he says is correct, but I can see at least one case where he is wrong, based on something like his example d.
For example, here is his Example b, \((x-2)^2(x+3)^4+2\):
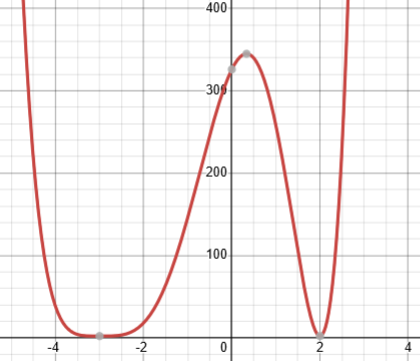
This has no zeros; the gray dots at the bottom are turning points with \(y=2\). By ignoring the “\(+2\)”, he shifts it down so that it has even zeros at \(-3\) and \(2\). The function as written has three turning points, but no zeros, so the formula would give \(Z-1+E=0-1+0=-1\). Shifting changes it to \(Z-1+E=2-1+2=3\).
Here is the graph of Example d:
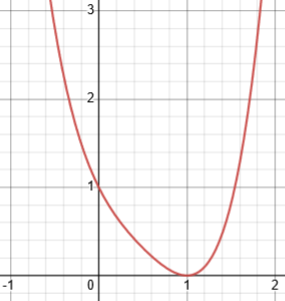
It has one turning point and one (even) zero, making \(1-1+1=1\). But it also has two non-real zeros, (\(i\) and \(-i\)).
Here is a polynomial like Doctor Rick’s example:
y = (x-1)(x+1)2 + 3
Mr. Kumar would get the right answer: The form (x-1)(x+1)2 has 2 zeros, one of them even, so T = Z – 1 + E = 2 – 1 + 1 = 2.
Here is the graph of the shifted function, \((x-1)(x+1)^2\):
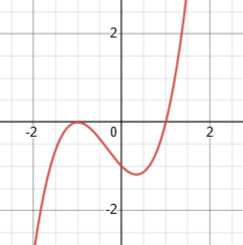
He gets the right answer only because of the unstated twist to his formula, that he allows himself to ignore an added constant, in effect shifting the function up or down to meet some unstated requirements.
But a polynomial can be written in more than one way; if the formula is valid, it should work regardless of how the function is written! We can expand my function to $$y=(x-1)(x+1)^2+3=x^3+x^2-x+2,$$ and then factor it, so there is no additive constant to ignore:
But it can also be expanded and factored as
y = (x + 2)(x2 – x + 1),
and if we apply the same formula to this, we see one real zero (and two non-real zeros), giving T = 1 – 1 + 0 = 0. This is obviously wrong.
So he is either making a totally unsupported claim (which, in mathematics, amounts to lying), or omitting the conditions under which his formula would work.
A formula that only works under unstated conditions can’t be called true, because one can’t even try to prove it. This is why theorems are always stated as precisely as possible.
Debarghya replied, first to Doctor Rick, and then to my comments on the video:
The first approach to the question ‘polynomial functions of odd order have at least one zero’ is straightforward and I must have understood that. it was my fault. but the approach using fundamental theorem of algebra is new to me. I know this theorem but not in detail. I will study more about this theorem to understand this approach.
Yes, this is the video that I referred to. There is no solid logic for this formula and hence cannot be trusted. Thanx again for your constant guidance.
The error had already been pointed out
I looked a little further, and realized that the error was already known, and an attempt had been made to specify conditions:
I just noticed that in the description of the video, it says,
CAUTION: The formula discussed for the number of turning points will not work when we have imaginary roots. It always works for Real roots. Thanks
It looks like this results from a discussion in the comments:
It does seem clear that he never made an attempt to prove his claim, but based it entirely on examples. This is unfortunate, considering his self-description as having a “Passion of sharing and guiding students to understand mathematics concepts and solve problems using different strategies”.
Here is the graph of commenter Eric’s example:
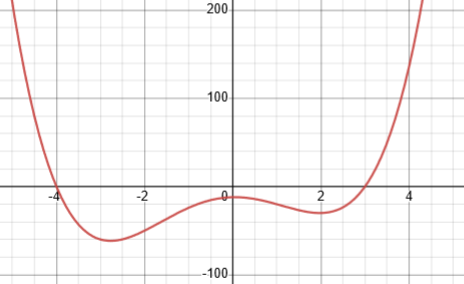
We could, in principle, rewrite this in a form that Mr. Kumar’s method would work with, by adding 20 (so that the x-axis intersects the curve between the turning points), factoring that, and subtracting 20. Unfortunately, the factoring would involve irrational numbers.
It seems clear that Mr. Kumar obtained his formula by extrapolating from a collection of nice graphs (the sort we give students to work with because everything is visible), and didn’t try cases like this where complex roots distort the graph, making extra turns.
But what of his new claim, that the formula always works “for real roots”? Presumably he means, “when all the zeros of the polynomial are real“. In Eric’s example, it is easy to see from the equation he gives that there are non-real zeros, since one factor is the irreducible polynomial \(x^2+1\); but the same is true of Example d, where the formula happened to work.
It seems that his real claim is that when a polynomial is written in factored form, with only linear factors, the formula applies; and since adding a constant doesn’t change the number of turning points, it can also be applied when a constant is added to such a product of factors, by ignoring that constant.
Lessons to learn
Debarghya agreed:
I have just seen the comments too…and truly surprised… I have to be more cautious while seeing videos…although I always judge every step while seeing any solution and seek your help whenever there is any doubt…but there are so many people out there who regularly see many such videos available free on YouTube…in that respect it has dangerous impact on learning mathematics…
In the comment section I see this part
There are many good teachers on YouTube and elsewhere, but I worry when I see how many students’ first thought on seeing a problem they can’t immediately solve is to search for random people who claim to have answers, rather than sticking with one or two trustworthy teachers. (And even then, the best of us make mistakes from time to time, so your habit of checking is a good one._
I responded:
I hadn’t noticed that comment. It gives me a couple thoughts:
First, he thought he had derived a valid formula, but what he had done was not a proof, and he apparently didn’t realize that. This is why I tend to avoid answering questions with a definite answer if I haven’t proved it! Even in what I’ve said to you, you may observe that I said, “I think all his examples are correct, but they do not exhaust the possibilities.” That is because I didn’t want to take the time to graph each of his functions and confirm his answers, even though I had thought about each of them and was reasonably sure! I also said, “I don’t know exact conditions under which what he says is correct.” I had some thoughts about that, but …
Mathematicians, at least in principle, tend to have a strong sense of their own fallibility, and avoid making strong statements without proof. (That sometimes bothers my friends in non-mathematical discussions, when I avoid committing myself!)
For some related ideas, see Why Do We Need Proofs?
Second, there are two ways you might use this as a learning opportunity. One is to ponder how he might have developed his formula from his examples. Why, given some assumptions about the form of a polynomial (in factored form, with linear factors so you know all the real roots) would his formula work? I haven’t considered it in detail (yet), but after trying a couple of the examples, I had a general sense that it was reasonable under some conditions. Can you see that? (If Mr. Kumar had told that story, rather than just tell people that his formula is true – in several videos, by the way, not just this one! – then it would have pedagogical value.)
In teaching, we sometimes just want students to learn facts (and that seems to be the focus in some educational systems); but what we should be primarily teaching is how to think; and telling the story of his discovery, in a way that would also reveal its limitations, would be far more useful than a formula – even if it did always work.
Another thing to do is to try extending the idea (as Eric Bian did, but failed), to determine either what the exact conditions are, or how pairs of complex roots might fit in. It happens that our post John Conway on Thinking and Teaching sort of touches on this issue, and you may find parts of it interesting.
In particular, that post demonstrates how a master teacher told a story (showing his actual thinking as it happened, including the occasional error) rather than giving an answer. But the context is a discussion of how complex roots reveal themselves on a graph.
Debarghya found another of Mr. Kumar’s videos:
Here is Mr. Kumar’s observation
Here he is doing something closer to telling his discovery story, but unfortunately he doesn’t notice that all his examples have turning points separated by zeros, and he ends with “You’ll always get the right results.”
I answered:
His thinking, as I expected, is entirely based on extrapolation from examples, without considering whether his examples cover all possible cases. This is a kind of thinking that is encouraged too often even in American schools (looking for “patterns” without proving them).
If I were him, I would have wanted an actual proof, which would turn out to require some explicit conditions. We can see that he is missing the possibility of turning points that are not between zeros, as in my example, or more than one turning point not separated by zeros; he would (hopefully) have caught that if he had attempted a proof.
I might have started my attempted proof something like this:
If a polynomial has Z zeros, of which E have even multiplicity, and T turning points, I claim that T = Z + E – 1.
Proof: Between any two zeros there must be a turning point. If all the zeros had odd multiplicity, then zeros and turning points would have to alternate*, like z-t-z-t-z-t-z. There can be no turning points beyond the last zero in either direction*, because that would require another zero beyond it. Clearly in this case there will always be one more zero than turning point, so T = Z – 1. But since an even zero is itself a turning point, we need to add the number of these to the number of turning points, resulting in T = Z – 1 + E.
I put an asterisk (*) next to two statements there that are false.
It’s true that the graph must turn (at least once) between any two zeros; but it is possible to have more than one turning point between two zeros, as in Eric’s example, or between the last zero and infinity, as in Doctor Rick’s. My first attempt at a proof would have made me think more fully about all the possibilities, which would help in refining my claim.
This is not yet a genuine proof, so I’d look for ways to prove claims such as “Between any two zeros there must be a turning point.” In thinking about that, I would realize it needs to be changed to “Between any two zeros there must be at least one turning point,” and, “Beyond the last zero, there must be an even number of turning points.” This allows for arrangements like z-t-z-t-t-t-z-t-t, which violate the two asterisked claims This changes everything; the proof fails in the general case.
I don’t know how general we could make the conditions; but Mr. Kumar is right in his correction, that if we make a strong condition that all zeros must be real, then his formula will work. I’ll leave that to the reader to try proving. (But I have completely convinced myself that it is true before publishing this claim!)