(An archive question of the week)
When I heard Thursday that the great mathematician John Conway had died (see the New York Times obituary here), I recalled not only his books I have read, but his involvement in Ask Dr. Math‘s early days. In addition to a couple dozen quotes from him, there were several questions in the very beginning of the service that he answered directly, probably through his heavy involvement in online math discussion groups. I want to look at one of his contributions that particularly demonstrates the kind of teacher he was (and his sense of humor).
If you bog down in the specific problem in view, skip to the last half of this post for his ideas on thinking and on teaching for understanding. That is the part I consider most interesting; but as the last half is comments on how he came up with his answer off the cuff, I can’t just skip to that without losing essential information.
An intriguing high school question
This question came on what I believe was the very first day of the service (November 1, 1994), and brought in not one but two professors to discuss it. I’m going to skip over others’ contributions (it was a long discussion that is too big for a normal post even now) and focus on Doctor Conway’s. Here is the question:
Wiggles on graphs, and complex roots
Complex Roots We know it is possible to look at the graph of a polynomial and tell a great deal about its real roots by looking at the x-intercepts. What can be discovered about a polynomial's complex roots by looking at the graph? There seem to be some interesting "wiggles" at locations that appear to be related to the "average" of the complex pairs. Do you have any insights regarding this topic? Best Regards, Pre-Calculus Students J.C.M. High School Jackson, TN c/o Phillip Scott
Doctor Ethan elicited some specific examples from Mr. Scott:
One example is:
x^4 - 6x^3 - 22x^2 + 56x - 64
This polynomial has a pair of complex roots (1 + i) and (1 - i). The average of these two roots (R1 + R2)/2 is the real number 1. If you look at the graph of the polynomial, there is "hill" very near x = 1.
Another example is:
3x^4 - 4x^3 + 3x - 4
This polynomial has a pair of complex roots (1 + i*sqrt(5))/2 and (1 - i*sqrt(5))/2. The avg. of these two roots is the real number (1/2). If you look at the graph, there is a very slight "wiggle" near x = (1/2).
Here are their graphs, with red dots at the points of interest:
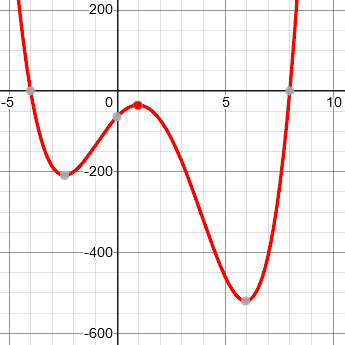
$$y = x^4 – 6x^3 – 22x^2 + 56x -64$$
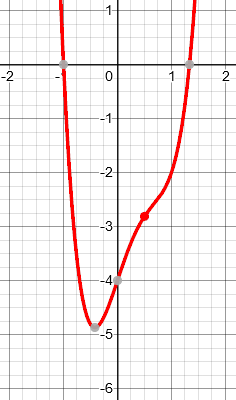
$$y = 3x^4 – 4x^3 + 3x – 4$$
In a couple days professor Stephen Maurer of Swarthmore College (then the host of the Math Forum and Ask Dr. Math) joined in with some thoughts; then on the 6th Prof. Conway wrote (dealing only with cases like the first). In passing this on (because of course he wouldn’t have been registered as a regular Math Doctor), Steve Weimar, who headed our service, prefixed it with this:
(Well, you guys really hit pay dirt in the responses you've received! You may not realize just how amazing these are until you hear that Prof. Maurer is a professor at Swarthmore who is a leader in the field of Discrete Math and John Conway, who wrote this letter, is one of the most famous mathematicians living. I hope you'll contact both of them personally to let them know what you've done with their answers and what you think of their communication to you. -- steve)
Conway started by answering the wrong question (which can be illuminating):
A very interesting question! At first I misread it as asking what we can tell about the non-real roots by looking at the x-intercepts of its graph, so let me answer that one first - essentially nothing! (this is because if a,b,c,... are the x intercepts of y = f(x), then all we can tell is that f(x) = (x-a)(x-b)(x-c)... times some g(x) which has only non-real roots, and of course, you can make the roots of g(x) be any collection of pairs of conjugate non-real complex numbers.
(Below, he will be commenting on how he wrote this, explaining that it is more or less stream-of-consciousness, written as he thought; I won’t make as many comments of my own as I usually do.)
Now back to the original question. I think we must add the information that the degree of the polynomial is some known number, if we are to read off information very easily. Also, let's think what we mean by "looking at the graph". If we are allowed to make very precise measurements on the graph, then we can work out (in theory) just what function f(x) is, and so all its roots are actually determined by the EXACT shape of the graph. If you know the degree is n, you only need to measure n+1 points to be able to work out, at least in theory, all the coefficients of f(x). So are question is really a rather loose one - just take a casual glance at the picture, for example, see where the wobbles are, and use what you see to produce an "engineer's guess" at the complex roots.
The quadratic case
Let's start with n = 2, and the equation y = (x-a)^2 + b. I'll suppose b > 0 to stop the roots from being real. Of course the roots are a +- root(-b), so we look for geometrical interpretations of a and b. Easy - a and b are the x and y coordinates of the minimum. So First easy theorem. If y = x^2 + ... has non-real roots, these are a +- root(-b), where (a,b) is its minimum. Corollary: If y = kx^2 + ... has non-real roots, these are a +- root(kb), where (a,b) is the minimum.
This gives the complex roots, if you know the leading coefficient k. (We’ll be correcting a small error here; he’s human! If he had explained his thinking, he might have pointed out that when a function is multiplied by k, that multiplies every y coordinate by k, including b; so that the “b” in the original function to which the theorem applies is actually b/k as we measure it on the graph. Therefore, the roots are \(a\pm\sqrt{\frac{b}{k}}\).)
So we need also an engineer's way of evaluating k.
Here it is - k is the amount y would increase if you went 1 unit left or right of the minimum.
This gives us the engineer's rule for quadratics:
The real part is the x-coordinate of the minimum. The [imaginary] part is the geometric mean of two numbers you can see in this little picture:
| |
| |
\ /
______\________/______
\ /
\____/
_______________________ x-axis
The two numbers I mean are the height of the minimum, and the "extra height" above that, that's cut off by the horizontal line that meets the curve 1 unit left and right of the minimum.
I never knew this before, although I did know that something vaguely like it was true.
Here is a better illustration:
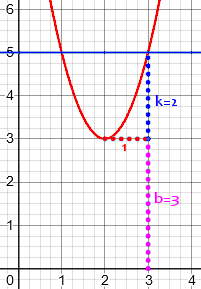
Here the minimum is at (2, 3), so a = 2 and b = 3; k = 2 is the blue vertical dotted line, the rise from the vertex at 1 unit left or right of the vertex. The real part of the complex root is a = 2, and the imaginary part is not the geometric mean of b and k, as he said, but of b and 1/k, that is,\(\sqrt{\frac{b}{k}} = \sqrt{\frac{3}{2}}\). In fact, the equation is \(y = 2(x-2)^2 + 3\), and setting this to zero yields \(x = 2 \pm \sqrt{\frac{-3}{2}} = 2 \pm i\sqrt{\frac{3}{2}}\).
The general case
Now what about more general polynomials f(x). Well, really the quadratic case is all there is, in a sense, if you're only taking a rough glance. Let me explain why.
Take your curve y = f(x), and fix your attention on a given minimum. Let y = q(x) be the best quadratic approximation near that minimum. Let's suppose for simplicity that the minimum is at x = 0.
Then the curve y = a + bx + cx^2 + dx^3 + ...
will be quite well-approximated by
y = a + bx + cx^2 (period)
near zero. So at the complex roots of the latter equation, f(x) will be quite near zero, so we can expect nearby roots of f(x) itself.
So my exact "engineer's rule" for the quadratic will work roughly for any polynomial.
Note that he has expressed this in terms of behavior near zero, knowing that is sufficient as the function can be translated into that position without changing the quantities he’ll be looking at.
We can apply this to the first example above, \(y = x^4 – 6x^3 – 22x^2 + 56x -64\), which has a vertex (in this case a maximum) near x = 1. We can’t read off y accurately from the graph, but plugging in x = 1, we get the (approximate) point (1, -35).
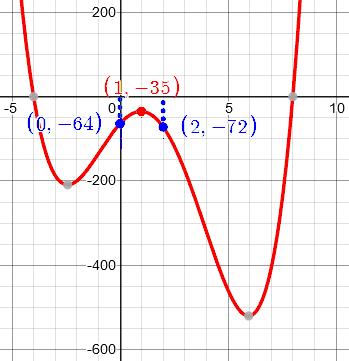
Looking one unit left and right from there, y = -64 and -72. These are not exactly equal, but the two drops are about -29 and -37, so we can use their average, -33, for k. So we have \(a\approx 1, b\approx -35, k\approx -33\). Using our corrected formula, we expect zeros with real part about 1 and imaginary part \(\pm\sqrt{\frac{-35}{-33}} \approx \pm 1\).
What are the actual roots? Dividing out the factors corresponding to know real roots -4 and 8, we are left with the quotient \(x^2 – 2x + 2 = (x – 1)^2 + 1\), whose zeros are … \(1\pm i\). Not bad!
Notice that Conway’s ideas don’t apply to the second example, with a mere wiggle. That case was discussed by the others in the thread. Given that we have a turning point to look at at all, he next considered how far from it you can do his measurements:
However, you should be prepared to work at the appropriate scale. Let me discuss this. If I take a horizontal line a bit above the minimum (a,b) that cuts the curve roughly where x = a +- c, then the imaginary parts of the corresponding pair of roots will be the geometric mean of the two heights I mentioned, MEASURED IN UNITS OF c. How can you tell roughly what is the right scale? Well, at least you can tell if it's going wrong. If the horizontal line you take hits the curve at a - c1 and a + c2, where c1 and c2 are very different, you know the quadratic part is NOT a sufficiently good approximation out to this distance, and you'd better beware. On the other hand, if the curve looks very like a parabola for quite a long time around the minimum, you can guess the corresponding pair of roots with fair confidence.
Here we are reversing the process; rather than going 1 unit left or right from a vertex and looking at how far we move vertically, we are going some distance d above or below and seeing how far it goes horizontally, c. When c was 1, k was d, and the imaginary part was about \(\sqrt{\frac{b}{k}}\). With a different horizontal distance c, \(d = kc^2\), \(k = d/c^2\), and the roots are \(a\pm\sqrt{\frac{bc^2}{d}} = a\pm c\sqrt{\frac{b}{d}}\). (You can see the scaling by c.)
Let’s try it on our example. …
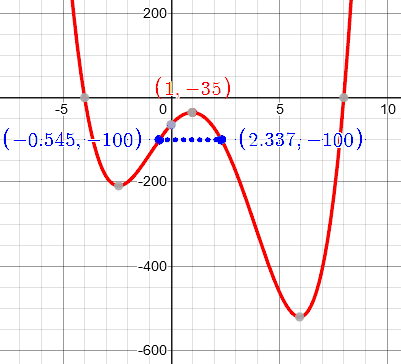
Here \(d = -65\), \(c_1 = 1.545\), and \(c_2 = 1.337\). These are reasonably close, and average about 1.4; so the imaginary part of the root should be about \(\pm 1.4\sqrt{\frac{-35}{-65}} = \pm 1.03\). Again, not bad.
In summary: if you are allowed to make precise measurements on the curve, then all the roots are in fact completely determined. If near some minimum the curve looks like a parabola out to a distance d (say), and my quadratic "engineer's rule" gives roots whose imaginary parts are less than d, then it's probably going to be pretty close to the truth. What information can you get from other features, say from points of inflection? Well, these first arise when f(x) is a cubic polynomial, so you'd answer this question by working out in detail what happens in the cubic case, and then if f(x) doesn't look like a quadratic for long enough, but does look like a cubic, you could confidently use your "cubic engineer's rule".
We can see here that Conway has been giving, not a complete answer, but suggestions about how to approach the problem, starting with a simple case and looking ahead toward a potential full answer. That is really what is most important in helping these students!
Thinking through his thinking
Shortly after his initial response (perhaps in response to thanks from the class), Conway discussed how he wrote his answer, moving from intuition to specifics:
Yes, I learned something, too! I already vaguely "knew" something about how the complex roots were related to the shape of the graph, but had never thought about it in detail. But to explain something to somebody else, you MUST really understand it yourself, and in full detail. This is why I LIKE all of elementary mathematics, even though I really AM a professional mathematician. In this case, I sat at this machine typing out an answer (I'm quite proud of the fact that I just came up with the answer as I was writing it - I only had to step away briefly to the blackboard to draw the general quadratic - otherwise it came straight out).
Real mathematics requires delving into details; but creativity starts with intuitions. How does one develop, and then pursue, such intuitions?
It might help to follow my thoughts, which were: i) CAN you do this? Is the desired information really there? This led to my remarks that from the x-intercepts you CAN'T determine the non-real roots, but from the exact curve you CAN. (That, to me, was the trivial bit.)
This is an example of a plausibility check, to focus one’s efforts.
ii) A minimum just above the x-axis obviously (to me) corresponds to a conjugate-complex pair of roots with small imaginary part (because if it were just below, they'd be real, and coincide if just one, and I know how pairs of real roots become pairs of complex ones "through" a coalescence).
This visual intuition comes from familiarity with quadratic functions, which starts with what I call “play”, just as children become familiar with the physical world through play.
The standard case of this is the quadratic one, so we'd better iii) work out the exact rule in the quadratic case! (which I'd never done before). This wasn't too hard.
A standard concept in problem solving (cf. Polya) is “try a simple case”. Here, the goal is an approximation, but understanding of that can be rooted in an exact solution.
Then iv) (which I really was aware of during ii) and iii)), the general case really IS the quadratic case, because in any given small region, your polynomial will be quite well approximated by a quadratic.
This intuition encapsulates the idea of Taylor polynomials.
Finally v) (which I'd never thought about before) can we guess roughly how far this quadratic approximation will work? If f(x) = q(x) + r(x), where q is the quadratic approximation to f, then (supposing the real part of the roots is 0), we can expect the size of r(iy) to be about the same as that of r(y) [because the dominant term of r(y) will probably be the first one, eg 5y^3, and this doesn't change in size if we replace y by iy]. This led to my rule of thumb that if it looks like a parabola out to a distance of about d, then our engineer's guess will be OK so long at it gives imaginary parts less than about d in size.
A deep knowledge of approximations includes knowing the importance of the magnitude of errors.
Then as a sort of PS I added vi) some general remarks about how one would develop better approximate guesses corresponding to higher-degree approximations. [All immediate to a professional.]
Once you’ve answered the basic questions, you can always map out possible future analyses.
How to teach mathematical intuition
Now he turns from teaching to giving advice about teaching, which to me is the most valuable part of Conway’s comments.
What's hard about learning mathematics (for a student), or teaching it (for a teacher) often is this "feel of the problem" stuff. What's this problem REALLY about? - sort-of-thing. It seems to be easy to learn how to manipulate formulae, but very very very hard to develop this "feeling" skill, and so it must obviously be very hard for teachers to learn how to teach this "feely" activity. Some ideas I use in this connection might be valuable.
How do you learn to understand beyond mere formulas? How do you help someone else do so? That is our real goal.
[Of course, I usually teach VERY bright undergraduates and graduate students - not exactly a typical audience - but I'm also quite good at teaching more typical "students", right down to very young children. I honestly believe that the real teaching problems are almost always the same, so I'll pass on my ideas anyway.]
I love that Conway can communicate clearly at any level; I, too, have found that teaching skills that work best for adults also work well for children.
When you teach something involving a formula (or, if we're talking about very young children, some concept that's a bit more abstract than they're used to), always
1) Find a picture that relates to the formula, and teach both at once. If there are several really different "pictures", teach a few of them (unless this might lead to "overload".
PLEASE do that!
Something visual gives us a place to hang abstract ideas that can’t be pictured. Even in grad school, I recall being impressed that the right picture let me think coherently about infinite-dimensional spaces, which in themselves can’t possibly be pictured!
2) Have lots of examples involving these pictures, and get the students to understand how the picture changes as the parameters in the formula [or maybe, the formula itself] changes.
Multiple examples are like looking at the same object from different perspectives, just like a child turning a block in different directions and trying different movements with it. Real understanding can’t come from only one direction!
3) Find what are the most important parameters! I mean the ones the engineer wants to know first, so that he can tell whether the cost is going to be millions of dollars, or only thousands. Don't worry too much about the things that will only affect the "conceptual price" by a few cents. [To use an example that came up in another one of these problems, every adult knows which are the most important digits in a price of $496.25. By the way, in that "rounding" problem, one should of course use the children's own developing "feel" for real prices - this might very well help them to stop rounding (say) this price to the nearest $10 and getting $90.]
When you have learned what makes the most difference, you can ignore inconsequential details (for the time being) and focus on what matters most. This is an important aspect of intuition, often thought of as “number sense” in children.
4) Use any "feel" for things that your students have already developed, for example this feeling for real prices, or what you've taught them in similar contexts earlier. [This will also help them to firm up on those earlier things.]
Connecting a new concept to familiar concepts helps make the new ones familiar, too.
5) Occasionally ask the students for information about teaching methods! (I've done this with 3-year-olds to very good effect.) Of course, you don't just ask them how you should teach such-and-such. And only for quite articulate students should you even ask which way they thought was best, when you've done something two ways, or done two similar things in different ways. But any good teacher will find all sorts of ways to "ask" the students which way was best. Children love to see their suggestions taken seriously, and affect the entire class.
This last idea of using the student’s own ideas, leads to a wonderful twist:
The place of fakery in teaching
If you forget everything else here as a teacher, let this remain with you:
Marx was a great philosopher, even though not all his ideas have stood the test of time. One I think that really has is when he said something like "Honesty, and Sincerity are two of the most important things in life." "So, if you can fake those, you've got it made!" I often follow Groucho's advice in teaching. I often teach when I'm tired, or teach subjects with which I'm thoroughly bored. So I just fake liveliness, or fake a total fascination with the subject I'm bored with.
I’ve read this piece many times, and I am always caught off guard by the joke.
But the principle is one I use heavily: When I teach or tutor, I want to make my interest in both the subject and the student tangible; a good “deskside manner” is essential. Sometimes that takes a little deliberate effort.
Often, when a student suggests some way I should do things, I "fake" a way of following this suggestion. The easiest one is when Sally suggests something I was going to do anyway. I say - "great" "We'll do it Sally's way! What a really wonderful idea!" and then every now and then call this "Sally's method". I have no moral qualms whatever about that one. The one that might get me burnt in Hell, or at least earn the disapproval of other teachers, now I'm letting the cat out of the bag, is when Jim suggests something, and I really don't do it, but find a way to pretend I do. In defence, let me say that I only do this sort of thing when Jim's suggestion is really a good one, given Jim's knowledge, but as a practical matter wouldn't quite work. The fakery is usually to modify Jim's idea a bit, to the nearest idea that does work, and quietly ignore the necessary modifications.
Find what the student has done well, and make that visible! When they think like a mathematician, even just a little, we need to make them feel successful, so they’ll want to do it again. And when an idea came from them, even only partly, it belongs to them.
In the hope that it will help me to gain absolution for this sin, let me say that I'm usually not quite so enthusiastic about Jim's ideas as I was for Sally's. I might say "That's a very good idea, Jim. Let's see how it works." but after that, it's just like my treatment of Sally's. Of course the thing that really pleases me no end is when Manuel produces a teaching idea (or any other idea) that I've never even heard of before. But strangely enough, Manuel's idea doesn't get too much more of a star billing than Sally's. The reason is partly that it really was very clever indeed for Sally to come up with even the standard idea, so she fully deserves her praise. Another reason is that (probably) Manuel is a student who's getting plenty of praise already. Often more than half of the students produce ideas that really do affect the way the course goes, and most of the rest get that impression even though it might not quite be true. Suddenly, I'm feeling terribly guilty about this little fakery - maybe I should stop doing it?
Steve Weimar responded approvingly to these last comments:
I think an essential part of teaching is acting, and there are many forms of it which are just right for the classroom, but probably the most important is recreating the experience of the learner. If I didn't do this, I would not find the language that works for my audience half the time and I would also misinterpret more than I already do what the student meant. For those situations where we are covering well-trodden ground, acting is called for and it's a great art that not only is good for the students but renews the possibility of new insights for the actor as well. One of my main interests as a teacher is to model the process of thinking, and this means externalizing what is most often hidden from sight. Running excitedly with Jim's idea but taking it to a place different than he anticipated is not fakery but representing the process we've been through. By being enthusiastic about Jim's idea you convey the notion that it's good to trust one's instincts, that a good starting place is not necessarily what one uses in the final analysis. By thinking out loud and showing what to do with it to make it work, you show how to shape good ideas from a reasonable beginning. If I were you I would keep up the acting and let them see the process of deciding why something needs to be modified. They would not be very bright students if they did not know you were acting and did not appreciate the performance.
This correlates to our desire as Math Doctors to let a student do the work, so we can start where they are, and show how much can be accomplished using the insights they already have. We encourage them to try something, even if it will not work out, because just getting moving can take you to a place of further insight.
The discussion continued with further ideas about graphs of polynomials; but the comments on teaching by Prof. Conway were well worth the price of admission.
He will be missed.
