We’ve been looking at dissection puzzles, where we cut an object into pieces, and rearrange them. Here we’ll examine a mystery posed by two different puzzles, each of which seems to change the area by rearranging the pieces. The answer combines the marvelous Fibonacci numbers and [spoiler alert!] how easily we misjudge areas.
A puzzle that shouldn’t work
We got this question in 1999:
A Fibonacci Jigsaw Puzzle For a homework problem in math, our geometry teacher showed us a problem dealing with the area of a square and making it equal to a rectangle. The area of the square was 64 but by the time we got to the rectangle (using Area formula A = b(h)) it equaled 65. The question is where did the mistake occur? He had an 8*8 square, which he cut into 2 pieces; the areas of these were 24 and 40. Then he cut the rectangular 24 piece into a right triangle, and the 40 piece into a trapezoid. Each time both pieces were equal. (There were 2 equal right triangles and 2 equal trapezoids.) Each trapezoid and triangle was then matched, making a proportionally bigger right triangle. These two triangles were then put together to make a rectangle with a width of 13 and height of 5. This area then equaled 65, but it is physically impossible for this to happen. What am I missing? The figure looked like this: _ _ _ _ _ a/e _ line ac | | | entire area =65cm^2 | 40 | 24 | A_ _ _ _ _ _ _ _ _ _ _ _ _ D |f | | | | | | | | | | | | c | | e| f| | | | | | | | | | | | | | | | | - - - - - - - - - - - - - - - - - - - - - c/f B C Does this make sense to you?
The picture is hard to decipher if you are not already familiar with the puzzle. I’ll redraw it to look like our puzzles from last week, starting with the goal, which looks like this:
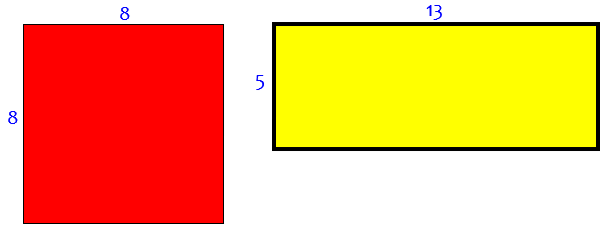
Can we dissect the square and cover the rectangle with the pieces? Of course not; The areas are 64 and 65 respectively. But we’ve been told we can do it this way:
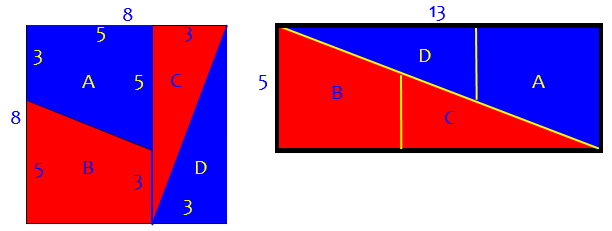
It looks good! But is it? (Hint: I cheated a little in my drawing.)
I answered:
Hi, Laik. My father-in-law made a copy of this puzzle out of wood, so I'm very familiar with it.
Here's a site by Ron Knott that explains the puzzle, but doesn't quite give the actual answer: Harder Fibonacci Puzzles Look for "A Fibonacci Jigsaw puzzle or How to Prove 64=65!"
(I’ve updated the link, which has been moved slightly in the intervening 20 years. And the wooden puzzle has moved from my in-laws’ home to mine.)
The trick is that in the rectangle, the diagonal line isn't quite exact: calculate the slopes of the segments Ae and eC, and you'll find that they are not the same; AeCf is really a very narrow parallelogram with area 1. See if you can calculate the area and prove me right. This is related to the Fibonacci sequence, as explained by Ron Knott, because the ratios of successive Fibonacci numbers, in this case 5:8 and 8:13, are close, approaching the golden ratio as you use larger numbers; that allows the slopes to fool you.
We’ll be looking at both slope and area calculations below.
The Fibonacci sequence is 1, 1, 2, 3, 5, 8, 13, … , where each number is the sum of the two before it. These numbers have many interesting properties. At the bottom of this post, I’ll include proofs of a more specific Fibonacci fact that applies to this puzzle. Observe, though, that \(\frac{5}{8} = 0.625\), while \(\frac{8}{13} = 0.61538…\). Close, but not quite. And the golden ratio is \(\phi=\frac{\sqrt{5}-1}{2} = 0.61803…\). (If you are familiar with \(\Phi = 1.618\dots\), that is the reciprocal of this lower case phi!)
A closer look
We got a similar question in 2001, but without the actual pieces:
Fibonacci Riddle An 8x8 square has an area of 64. We can cut the square into four pieces and reassemble to get a 5x13 rectangle with an area of 65. Where does the extra 1x1 square come from?
Doctor Tom answered first:
The pieces don't fit EXACTLY. I don't know what version of this problem you're working on, but you'll probably find that the triangles are not perfectly aligned, but it's hard to see the error, since it's spread out over a long line.
The misalignment would involve the slopes we discussed.
Doctor Rob joined in 20 minutes later:
Thanks for writing to Ask Dr. Math, Daniel.
If you check out the 5 x 13 rectangle, you will find that the pieces do not exactly cover the rectangle. There is a very narrow parallelogram with two opposite corners at opposite corners of that rectangle whose area is 1 square unit. That is because the slopes of the diagonal edges of the two kinds of pieces are not exactly the same, although they are close.
o---+---+---+---+---o---+---+---o
| | /|
+ + / +
| | / |
+ + +
| | / |
o.__ + / +
| `-.__ CD | / |
+ `-._ + AC +
| AB `--._ | / |
+ `-o BD +
| | / |
+ + / +
| | / |
+ + +
| |/ |
o---+---+---+---+---o---+---+---o
A
o---+---+---+---+---+---+---+---o---+---+---+---+---o
| `--.__ | |
+ `--.__ + +
| `--.__ | |
+ o--._ + +
| B | `--._ | C |
+ + `-o._ +
| | `--._ |
+ + `--.__ +
| | `--._ |
o---+---+---+---+---o---+---+---+---+---+---+---+---o
D
Like my drawing, this picture cheats a little, making ABCD look collinear:
The slope of AC is -3/8 = -0.375, and the slope of AB is -2/5 = -0.400. Thus <BAC is not zero, and B is slightly below line segment AC. Similarly, <BDC is not zero, and C is slightly above line segment BD. The narrow parallelogram is ABDC, whose area is 1 square unit.
In particular, the height of point B is 3, but the corresponding point on AC is \(5-\frac{3}{8}(5)=\frac{25}{8}=3\frac{1}{8}\), so the vertical error is \(\frac{1}{8}\).
Here are more accurate pictures, close up, to show that parallelogram:
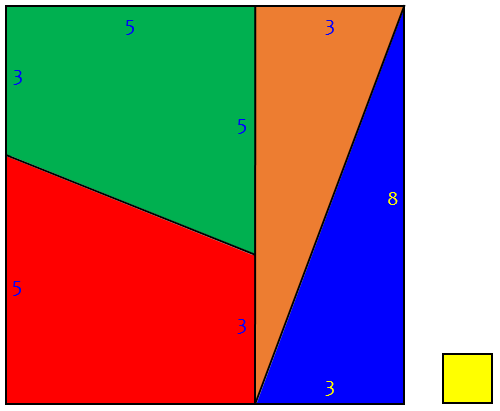
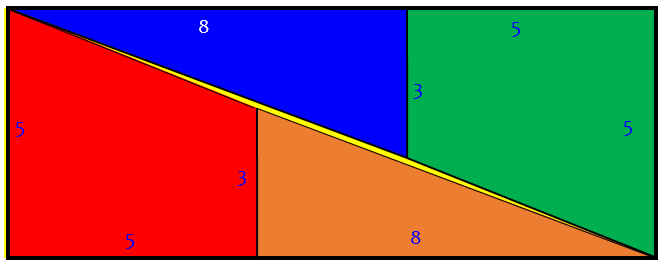
The yellow 1×1 square has the same area as the yellow parallelogram in the middle of the rectangle, as hard as that is to believe! Here is an exaggerated view of it:
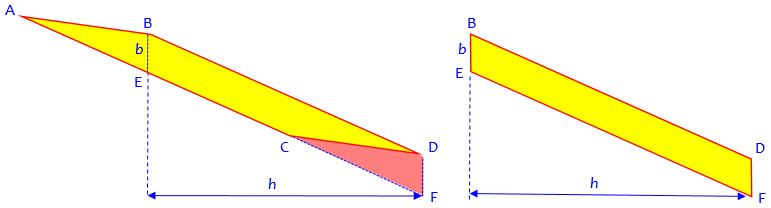
Here \(b = \frac{1}{8}\) and \(h=8\); moving ABE to CDF we keep the same area, which is equal to \(bh=1\).
Rather than slopes, we can also use lengths (via the Pythagorean theorem):
Another way to see this is that
AB = CD = sqrt(5^2+2^2) = sqrt(29) = 5.385165...,
BD = AC = sqrt(8^2+3^2) = sqrt(73) = 8.544004...,
AD = sqrt(13^2+5^2) = sqrt(194) = 13.928388...,
AB + BD = AC + CD,
= 5.385165... + 8.544004...,
= 13.929169...,
> 13.928388...,
= AD.
This proves that neither B nor C lies on line segment AD.
If C were on segment AD, then we would expect that AC + CD = AD. That fact that it is greater implies, by the triangle inequality, that ACD is a triangle.
The missing square puzzle
A similar but different puzzle was sent to us in 2002:
Magic Triangle Puzzle Hello, While surfing on the Internet I encountered a site with a triangle puzzle on it. The guy that put it on his site claims he has found a flaw in Euclidean geometry. You can view the problem here: Simeon's Triangle Puzzle It looks simple, but I just can't explain it. Can you tell me where that white square came from?
The site no longer exists, so I have removed the link. Several others have asked about the same puzzle by sending us a link to an image file called “bizare.gif” [sic] at various sites, and none of those still exist either. But the problem is mentioned on the R. Knott site referred to above, as Yet Another Fibonacci Jigsaw Puzzle. Here is the image from that page:
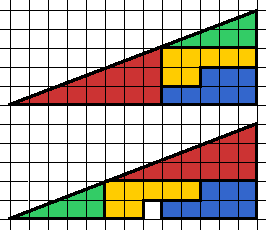
It appears that by rearranging the same four pieces they get an identical triangle, but with room for an extra square! Observing that the triangle has legs 8 and 13, which are divided up into parts of 2, 3, and 5, you might wonder if this, too, involves Fibonacci numbers. You’d be right! And the basic trick is similar. Can you spot it?
Doctor Nitrogen answered:
Hi, Pieter: I suspect the reason a blank white square appears in the bottom diagram is that in the top diagram, the green right triangle at the top and the red right triangle at the bottom are not similar triangles. As a result, the area of the entire figure does not remain the same when you move the two triangles.
If the triangles are not similar, then their slopes will be different, and the top edge of each figure will not be a straight line. The thickness of the black line contributes to covering this up; it’s drawn as a straight line but doesn’t actually pass through the vertices of the triangles.
Go back to the image and examine for yourself. This refers to the top diagram: The acute angle at the bottom left of the top green triangle is tan(beta) = 2/5, and the acute angle at the bottom left of the larger red triangle at the bottom is tan(alpha) = 3/8.
These tangents of angles could just as well be described as slopes.
Put another way, the two smaller sides of the smaller green triangle are 2:5, but the ratio of the sides of the larger red one is 3:8. Clearly, 2:5 =/= 3:8, and the red and green triangles are not similar. Why should this matter? Because if the red and green right triangles were similar, you could place the green one at the bottom left and the red one at the top right, and leave no blank white square when you moved the orange figure. But the triangles are not similar, so when you place the green one in the lower position and the red one in the higher position, you increase the total area of the larger triangle that contains the red and green triangle and the other orange figure.
Because the slope of the green triangle, \(\frac{2}{5} = 0.4\), is greater than that of the red triangle, \(\frac{3}{8} = 0.375\), the lower image has a “hump”, raising the “hypotenuse” enough to make room for the extra square, even though it doesn’t look like enough.
In fact, Doctor Ian suggests that for the two triangles to actually act as you see on that site, the big triangle that contains both of them (as well as the orange figure) would have to have a curved, concave-shaped hypotenuse in one case and a curved, convex-shaped hypotenuse in the other. I did not work out a formal proof for this; nevertheless, that's why I suspect the blank white square mysteriously appears in the bottom diagram. I hope this got you thinking on some intriguing math.
Here are accurate versions of the two pictures; the dotted lines are the true hypotenuse:
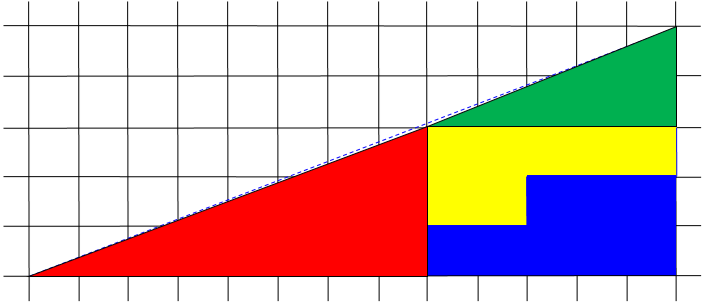
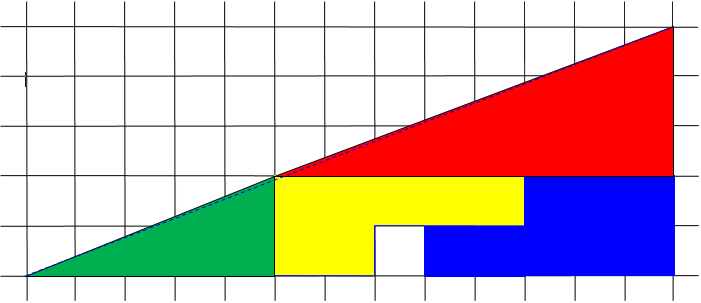
Another Math Doctor has suggested cutting the two figures, carefully drawn, from graph paper, and putting one on top of the other to compare more easily.
Doctor Ian simultaneously added his own ideas, filling in the proof:
Hi Pieter, Dr. Nitrogen's analysis is correct. The key is that the two triangles aren't similar. Here's how it looks to me. In the first triangle, moving from left to right, you move at one slope (3/8), and then switch to a steeper slope (2/5). This means that the 'hypotenuse' is not actually a straight line, but in fact is slightly concave. In the second triangle, the situation is reversed: you switch from a steeper slope to a gentler one, which makes the 'hypotenuse' slightly convex. In fact, then, neither of the 'triangles' is really a triangle at all, but a quadrilateral in which one of the angles is nearly 180 degrees. The thickness of the line is used to mask the change in slope; but the difference between the convex and concave 'hypotenuses' is the area of the white square in the bottom triangle. Does that make sense?
To quantify the error, in the bottom picture the top of the green triangle is at height 2; but the corresponding point on a straight hypotenuse, 5 units along at slope \(\frac{5}{13}\), would be \(5\cdot\frac{5}{13}=\frac{25}{13}=1\frac{12}{13}\), just \(\frac{1}{13}\) lower. So the “hypotenuse” bulges up by \(\frac{1}{13}\) over a width of 13 units, making a triangle with area \(\frac{1}{2}\) square unit.
Area calculations
Later that year, we got a comment from a reader, Michael:
Here is a numerical answer, easier to see for some kids: 13 * 5 / 2 = 32.5 square units. That's the apparent size of both combined (whole) triangles. But if you calculate the areas of each of the sections, again as they appear on the puzzle, they add up to 32 square units on the top one, and 33 square units on the bottom (the one with the white square in it). This confirms that the 'slightly concave, slightly convex' analysis is right, and that the hypotenuses of both triangles are not straight lines; both are arcs, with a net area of one square unit.
So the area of the triangle we think we see is the average of the two non-triangles that are actually there; and the difference between the two is that one extra square.
Doctor Schwa replied:
Thanks! Several of the answers we link to are somewhat similar to yours, but surprisingly none of them explicitly does the area calculation. I'd add some of supporting details to your calculation: Top "triangle" has: one 8x3 triangle, area 12 two "P" shaped pieces, total area 15 one 5x2 triangle, area 5 for a total of 32. Bottom picture has those same four pieces, plus the one square unit hole, for a total of 33. Thus neither of them can actually fill the 5x13 triangle exactly.
Why Fibonacci?
Let’s take a little look at why Fibonacci numbers work so well in these puzzles, in addition to the fact mentioned earlier that those dimensions result in similar slopes.
In 2002 we got this variation on the question, which wasn’t archived:
This is a question from my assignment which I don't understand why? Take any three consecutive Fibonacci numbers. Use the middle number as the sides of the square and the outside numbers as the sides of the rectangle. Why is there a difference of one in the calculated values of the area of the square and rectangle, but when divided up into pieces right, the pieces from the square fit exactly into the rectangle? That is the question I don't understand some help would be great.
Sebastian has not just been shown one example of our first puzzle (using 5, 8, 13), but was told that the same thing can be done with any set of three sequential Fibonacci numbers (like 2, 3, 5, or 3, 5, 8, or 8, 13, 21) and do the same thing – and the areas of the rectangle and square will always differ by exactly 1. But why? Can it be proved?
Doctor Rick answered:
Do you need help with both parts of the question, or just one? You can understand why there is a difference of 1 in the areas. First examine how it works in a few small cases: F[1] = 1, F[2] = 1, F[3] = 2 ==> 1^2 - 1*2 = -1 F[2] = 1, F[3] = 2, F[4] = 3 ==> 2^2 - 1*3 = 1 Notice that the difference is 1 in each case, but it isn't always the same area that is bigger! Once you see what is happening, you can write an inductive proof. For any k, assuming something about F[k]^2 - F[k-1]*F[k+1], you can prove something about F[k+1]^2 - F[k]*F[k+2]. Since the something is true for k=2, it is true for all k by induction. Why do the pieces from the square fit exactly into the rectangle? The answer is that they don't! If the pieces are cut the way I am picturing it, there is a diagonal cut. You'll find that the diagonal cuts are not quite parallel (how can you tell?), so that the pieces either overlap slightly, or they leave a narrow gap.
What we want to prove, in general, is $$F_{n-1}\cdot F_{n+1}-{F_n}^2=(-1)^n$$ That is, the difference alternates between \(+1\) and \(-1\). In our example, \(8^2=64\) is 1 less than \(5\times 13 = 65\); in the next larger size, \(13^2=169\) is 1 more than \(8\times 21 = 168\). We’ve had questions about the latter puzzle, too.
Proving it by an explicit formula
This fact was the subject of a question in 1999:
Fibonacci Trick I am interested in why the Fibonacci trick works. How do f(n-1), f(n+1), and f(n)^2 relate to each other? I am not a good math student at all but the Fibonacci sequence has really interested me. I have been working for a while on a way to solve this but I haven't gotten anywhere. Please help me! I would like to look at why this works and see if it helps to understand the ways the Fibonacci sequence shows up in nature, etc.
Doctor Anthony answered, using a known formula for the nth Fibonacci number in terms of the Golden Ratio φ:
For the Fibonacci sequence show:
[F(n+1) * F(n-1)] - [F(n)]^2 = (-1)^n
The expression for the nth term of the Fibonacci sequence is:
1 [1+sqrt(5)]^n 1 [1-sqrt(5)]^n
F(n) = ------- * ------------- - ------- * -------------
sqrt(5) 2^n sqrt(5) 2^n
I will write this in the form
1
F(n) = ------- * [P^n - Q^n]
sqrt(5)
1+sqrt(5) 1-sqrt(5)
where P = --------- and Q = ---------
2 2
Note that P+Q = 1
P-Q = sqrt(5)
PQ = 1/4 - 5/4 = -1
The numbers \(P\) and \(-Q\) are, respectively, the numbers \(\Phi\) and \(\phi\) we mentioned above. We’ll be looking at some aspects of the Fibonacci sequence soon, if this mystifies you!
We are asked to show that [F(n+1) * F(n-1)] - [F(n)]^2 = (-1)^n
[F(n)]^2 = (1/5)*[P^n - Q^n]^2
= (1/5)*[P^(2n) + Q^(2n) - 2*P^n*Q^n] ............(1)
F(n+1) * F(n-1) = (1/5)*[P^(n+1) - Q^(n+1)]*[P^(n-1) - Q^(n-1)]
= (1/5)*[P^(2n) + Q^(2n) - P^(n+1)*Q^(n-1)
- P(n-1)*Q^(n+1)] ............(2)
We need to show that the difference between these is always \(\pm 1\).
subtracting (1) from (2) we get:
(1/5)*[-P^(n+1)*Q^(n-1) - P^(n-1)*Q^(n+1) + 2*P^n*Q^n]
= (1/5)*[-P^(n-1)*Q^(n-1)*(P^2 + Q^2) + 2*P^n*Q^n]
= (1/5)*P^(n-1)*Q^(n-1)*[-(P^2 + Q^2) + 2*P*Q]
= -(1/5)*P^(n-1)*Q^(n-1)*[P^2 - 2*P*Q + Q^2]
= -(1/5)*P^(n-1)*Q^(n-1)*(P-Q)^2
but (P-Q)^2 = 5, so we obtain
= -P^(n-1)*Q^(n-1)
= -(PQ)^(n-1)
but PQ = -1 and so the difference between (1) and (2) reduces to:
= -(-1)^(n-1)
= (-1)^n
and this completes the proof.
Proving it inductively
The same fact was the subject of a question in 2001, without reference to the puzzle:
Fibonacci Identity I am trying to create an inductive proof for the particular identity of Fibonacci numbers that: F(n-1) * F(n+1) = (-1)^n + (Fn)^2 I know I do a base case of n being 0, and then an inductive step of n being n+1, but beyond that I just can't get the math to work out. Is this a valid identity, and if so, how would I work out the math to inductively show this?
Doctor Anthony gave the requested inductive proof :
Well, I suppose you have been able to show that this works for n = 0. Now we suppose that F(n-1)*F(n+1) = (-1)^n + (F(n))^2 holds for n. We can rewrite this to F(n-1) * F(n+1) - (F(n))^2 = (-1)^n [*] Now we will replace all n by n+1 at the left-hand side of the equation, and show that it yields (-1)^(n+1). For that we use the truth we suppose of [*] as well as application of the Fibonacci rule F(m+2) = F(m)+F(m+1) for all m: F(n)*F(n+2) - (F(n+1))^2 = F(n)*[F(n+1) + F(n)] - F(n+1)*[F(n) + F(n-1)] = F(n)*F(n+1) + (F(n))^2 - F(n)*F(n+1) - F(n+1)*F(n-1) = (F(n))^2 - F(n+1)*F(n-1) = -(-1)^n = (-1)^(n+1) And we get where we want to be.
We’ll be looking at inductive proofs soon. Here he has shown that if the claim is true for some given value of n, as it is for n = 0, then it is true for the next, and therefore for all subsequent values.

Pingback: What is Mathematical Induction? – The Math Doctors