Last week we looked at a puzzle about cutting a square cake into equal pieces. Here we will be trying to cut a rectangle into two pieces and rearranging them to make a different rectangle. Three of the questions we’ll look at came within two weeks in 2001, but we’ll take them in a logical order. As we do so, we’ll think about how to think.
Experimentation, then thinking
Our first question will provide an overview of possibilities:
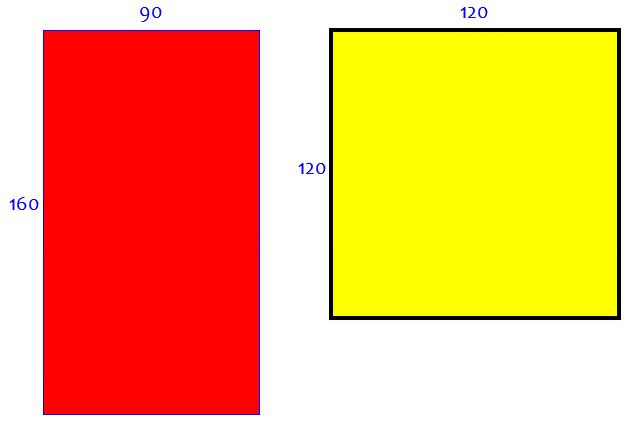
World War II Window Blackout During the Second World War, families had to black out their windows. Mr. Brown had a square window 120cm x 120cm, but the only material he could find was a sheet of plywood 160cm x 90cm; same area, different shape. He drew some lines and cut out just two congruent shapes, which he joined to make a square of the correct size. How did he do it? I have tried drawing sketches, scaled drawings, and cardboard cutouts, but I can't solve it. I see no way of doing it. Please help!
We are to cut and rearrange the \(160\times 90 = 14,400 \text{ cm}^2\) red rectangle to exactly cover the \(120\times 120 = 14,400 \text{ cm}^2\) yellow rectangle:
Doctor Ian answered, first showing how one might experiment with various possibilities to see what happens:
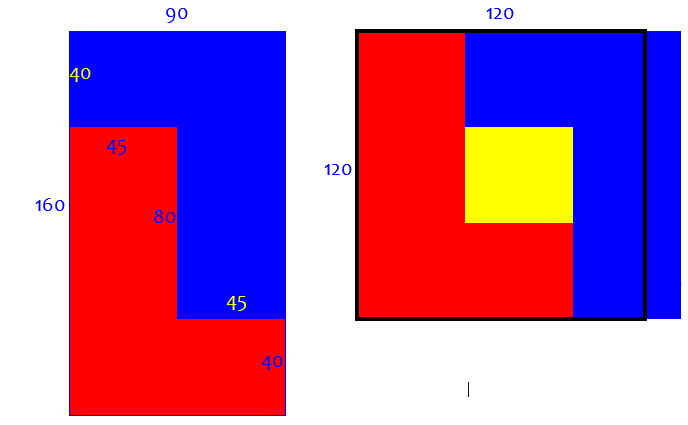
My first thought was that this would end up being two L shapes, e.g., +-----------+ | | | B | +-----+ | | | | | | | | | | | | | | | | | +-----+ | A | | | +-----------+ but that doesn't quite work. You always end up leaving a hole in the middle.
This sort of dissection can be useful in some problems; in fact, we’ll see something of this sort later. But here it fails, no matter how you choose dimensions:
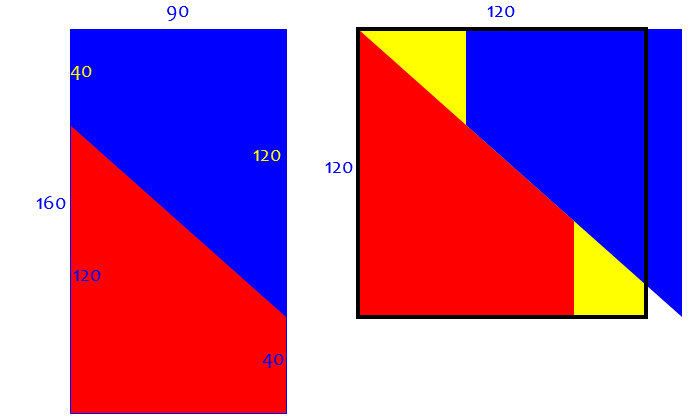
Then I tried trapezoids, +-----------+ | | | B | + | | . | | . | | . | | . | | . | | + | A | | | +-----------+ but that doesn't quite work, either. You always end up leaving a hole in the corner.
For example,
But these ideas suggest a generalization, with more (and equal) steps. We’ll see a way to decide how many steps we need later, but trial and error can lead to this:
Here is the general idea: +-----------+ | | | B | +---+ | | | | | | | | +---+ | | | | | | | | +---+ | A | | | +-----------+ By moving part B to the right and then down, you can make a square: +---+-----------+ | | | | | B | | +---+ | | | | | | | | +---+ | | A | | | | | +-----------+---+ I'll leave it to you to work out the dimensions involved.
Here it is, with appropriate dimensions, dividing the height into 4 equal parts, and the width into 3:
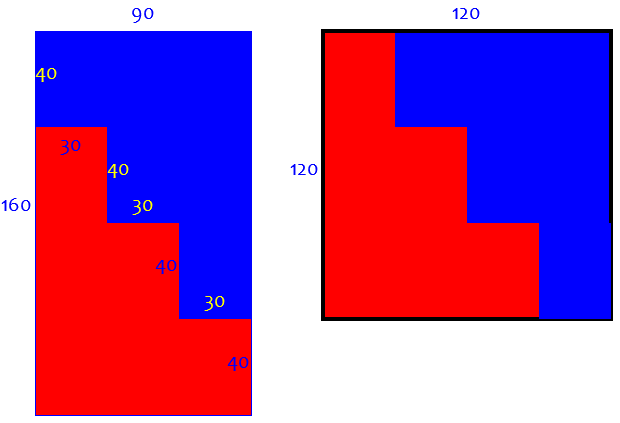
I finally came up with it by forgetting about the initial rectangle, and focusing on the final square. I knew I'd have to shift one of the pieces up and over to the left (do you see why?). I knew the base of A would be 90cm wide, which meant that the tip of B would have to be 30cm wide. The rest follows from the fact that the two pieces have to be congruent. This was a fun question to think about. Thanks for asking it!
It is very common to solve a problem by focusing on the goal, rather than what we have; or by working from both ends simultaneously. No piece can be wider than 90 cm to fit on the left, or higher than 120 cm to fit on the right; so we cut steps according to the difference between the piece dimensions and either whole.
Creating a general rule
Here is a similar question from 2004:
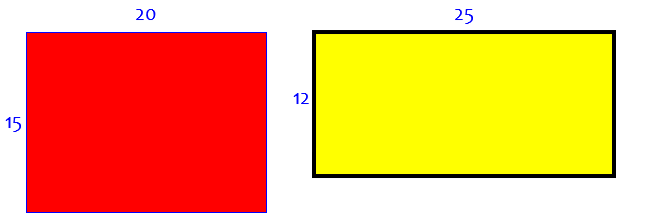
Using Dissections to Cut and Reshape Rectangles Cut a 20x15 piece of paper into two pieces to form a 25x12 piece. I have tried and tried and tried and my parents have tried also but we can't figure it out. This may be a trick question but I can't decide what the trick is. Can you help?
Again, we want to cut the red rectangle in two pieces and rearrange them to cover the yellow one:
Doctor Douglas answered, not with a solution to the given problem, but with a similar example, leaving room for Marcia to do some problem solving of her own:
Hi Marcia.
The trick is to use a stairstep-shape. Here's an example of a 20 x 12 rectangle rearranged into a 15 x 16 rectangle.
20 15
+----+----+----+----+ +----+----+----+
| | | | |
+ +----+ + + +----+
| | | 12 | | |
+ +----+ + + +----+ + 16
| | | | | |
+----+----+----+----+ +----+ +
| |
+----+----+----+
Can you figure out how to adapt this for your problem?
These types of problems are known as "dissections".
Here is that example:
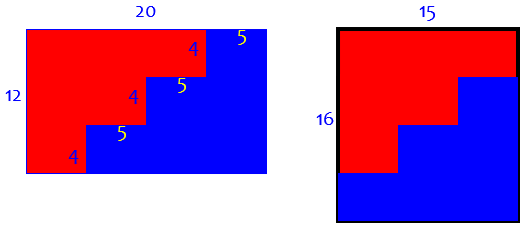
Now, how can we decide how many steps to make, and also whether to change the orientation before reassembling? Under what conditions can this dissection be done successfully? Let’s examine this example closely before trying to solve our problem.
We see that we are multiplying the width by \(\frac{15}{20}=\frac{3\cdot 5}{4\cdot 5}=\frac{3}{4}\), and the height by \(\frac{16}{12}=\frac{4\cdot 4}{3\cdot 4}=\frac{4}{3}\). These are, of course, reciprocals or the areas would be different. We decrease the width by subtracting one step width of 5 (the difference of the two widths, which is also a common factor), and increase the height by adding one step height of 4 (the difference of the two heights, and again a common factor). In general, it would look like this:
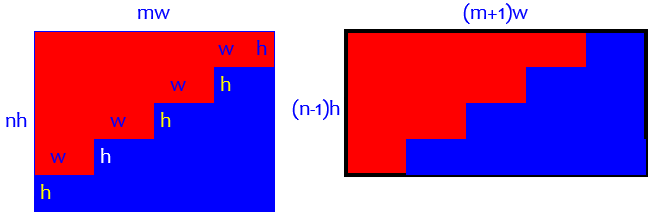
In the problem we are trying to solve, the widths are 20 and 25, which differ by 5, which is a factor of both; so we’d like our step width to be 4 (so w = 5, m = 4). The heights are 15 and 12, which differ by 3, which is a factor of both; so we’d like our step height to be 3 (so h = 3, n = 5). Let’s do it:
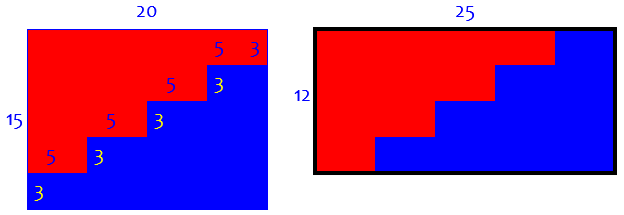
What if we’d been asked to turn a \(20\times 15\) into a \(12\times 25\)? Then we’d be decreasing 20 to 12, a difference of 8 which is not a factor of either; so we’d have to turn the target into the orientation we actually used.
Enlarging a carpet
The next question is more complicated; we’ll see three different descriptions of how to discover it. This is from 2001 again:
Carpet Problem You have to carpet a 9x12 room, but when you go the store they only have a 10x10 carpet and a 1x8 piece of carpet. If you add up the number of square units, then 10x10 and 1x8 = 108 and 9x12 = 108, so you know that it can fit. However, you can only make one cut in the carpet (meaning either entering one side of the carpet and exiting any side, or entering one side of the carpet and cutting over yourself). Where would this cut be to make the carpet fit in a 9x12 room.?
Here is the problem:
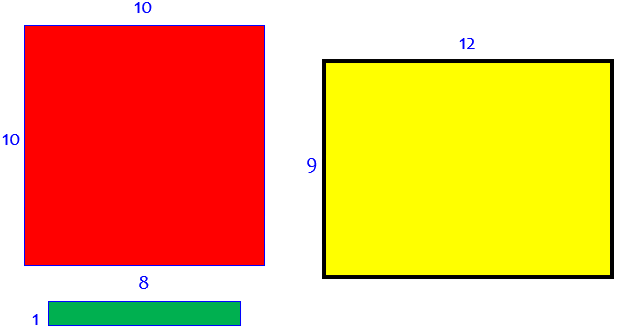
This received two answers. We’ll start with Doctor Greenie’s, which is only a set of hints:
Hi, Nathan - I have seen this problem posed many times, and the instructions are virtually never clear. For example, in your presentation of the problem, I don't know what "cutting over yourself" means. Here are a couple of things I think you need in order to have a chance of solving this problem: (1) You can only cut one of the pieces of carpet, giving you a total of three pieces. Putting the two original pieces on top of each other to make the cut is not allowed, nor is folding the piece you cut so that the single cut gives you more than three pieces. (2) You can't solve the problem by making a single straight cut. It has to be some sort of fancy zigzag cut. Note that for the resulting pieces to exactly cover a rectangular floor, the cut will have to consist of segments all at right angles to each other. Those are a couple of hints that might help you find the solution; but I suspect that even with those hints only a tiny fraction of students would be able to do so. (I never figured out the problem for myself - I had to be shown how it is done...)
Although we generally like to give only hints, it’s hard to give a good enough hint that isn’t too good!
Clarifying the problem
Doctor Rob had beat that answer by 3 minutes; he gave the actual solution:
Try this: o---+---+---+---+---+---+---+---+---+---o | | o---+---o + | | | + o---+---o + | | | + o---+---o + | | | + o---+---o + | | | + o---+---+---+---+---+---o + | | | + o---+---o + | | | + o---+---o + | | | + o---+---o + | | | + o---+---o | | o---+---+---+---+---+---+---+---+---+---o Slide the upper right piece two feet right and then one foot down, and see what happens.
Here is what happens (flipped side to side following the next answer we’ll see):
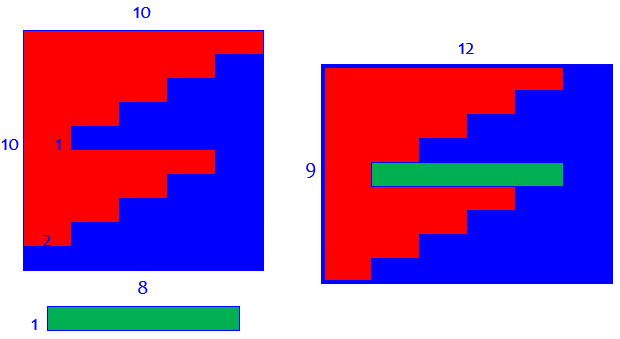
How could you figure it out?
But back in 1996, we had had the same question (which Doctor Greenie referred to as a last resort):
Cutting Carpet Two pieces of carpet are to be used to cover a floor. The two rectangular pieces are 1 ft by 8 ft, and 10 ft by 10 ft. You are allowed to make just one cut in one of the two pieces. The three pieces of carpet must then be arranged to fit a 9 ft by 12 ft floor exactly. Make a sketch that shows how this can be done.
Doctor Ceeks answered, describing the solution in words rather than try to draw it with text:
Because there is no way to fit the 10 by 10 piece into a 9 by 12 rectangle, it is the 10 by 10 piece which must be cut somehow. Here's how: I'll start by describing a walk starting at the lower left corner of the 10 by 10 foot square piece. up 1 foot. (no cut needed for this part) right 2 feet. up 1 foot. right 2 feet. up 1 foot. right 2 feet. up 1 foot. right 2 feet. up 1 foot. left 6 feet. up 1 foot right 2 feet. up 1 foot. right 2 feet. up 1 foot. right 2 feet. up 1 foot. right 2 feet. Here, you should have cut the square into two pieces, a left piece and a right piece. (you come out 1 foot below the upper right corner.) Now, slide the right piece over 2 feet and slide it up 1 foot. You will see a 9 by 12 foot rectangle with a 1 by 8 hole in the exact center!
What’s most important for us is his description of how he found the solution:
(I arrived at this solution by hoping for a symmetric solution...so I put the 1 by 8 strip in the exact middle of the 9 X 12 rectangle. Since I was hoping to deal only with integral length cuts, putting the 1 x 8 strip in as in the solution was the way to go.)
So this was the starting point, around which the solution crystalized:
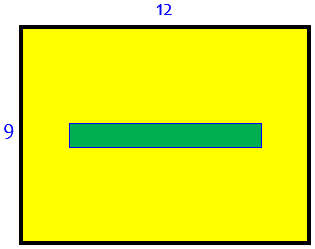
The rest would be the same zigzag concept we’ve seen before. Symmetry is often a good start!
A hole in the carpet
We’ll close with one final question, from 2001 again:
Carpet and Room Areas A man buys a roll of carpet 9 ft. wide and 12 ft. long to fit a room 10 ft. x 10 ft. When the carpet is unrolled, a rectangular hole 1 ft. wide and 8 ft. long is discovered in the exact middle of the carpet. The man decides that since the area of the roll is 108 sq.ft. and the area of the hole is 8 sq. ft., the carpet will still fit in the 100 sq. ft. room. How can he cut the roll of carpet with the hole in the middle of it into to two pieces that will fit into the 100 sq. ft. room when the two pieces are put together? I don't know where to start. Please help me.
You may see how this is just a reworking of that last problem! It’s just reversed. In fact, what we start with this time amounts to the seed of an idea that Doctor Ceeks used:
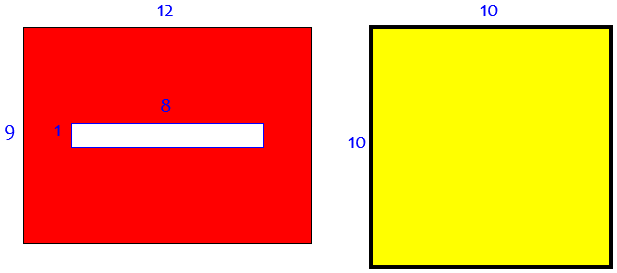
Doctor Rob answered, using a series of simpler problems to work up to the answer we’ve already seen:
Thanks for writing to Ask Dr. Math, Matt. Let's start with a smaller case: a 4-by-4 room and a 3-by-6 carpet, with a 1-by-2 hole in the middle: o---+---+---+---+---+---o | | + o---+---o + | | | | + o---+---o + | | o---+---+---+---+---+---o One should cut the carpet thus: o---+---o---+---+---+---o | | | + o---+---o + | | | | + o---+---o + | | | o---+---+---+---o---+---o Then move the right-hand piece 1 foot up and 2 feet to the left (to make the result 1 foot taller and 2 feet narrower), and you'll have o---+---+---+---o | | o---+---o + | | | + o + | | | + o---+---o | | o---+---+---+---o Ta-daaaa!
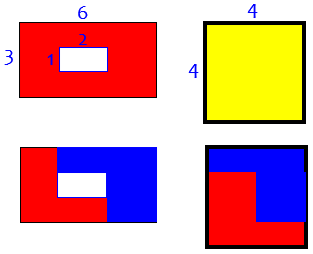
Now the next larger case, a 6-by-6 room and a 5-by-8 carpet with a 1-by-4 hole in the middle: o---+---+---+---+---+---+---+---o | | + + | | + o---+---+---+---o + | | | | + o---+---+---+---o + | | + + | | o---+---+---+---+---+---+---+---o The cuts should look like this: o---+---o---+---+---+---+---+---o | | | + o---+---o + | | | + o---+---o---+---o + | | | | + o---+---o---+---o + | | | + o---+---o + | | | o---+---+---+---+---+---o---+---o Then move the right-hand piece 1 foot up and 2 feet to the left (to make the result 1 foot taller and 2 feet narrower), and you'll have o---+---+---+---+---+---o | | o---+---+ + | | | + o---+---o + | | | + o---+---o + | | | + o---+---o + | | | + o---+---o | | o---+---+---+---+---+---o
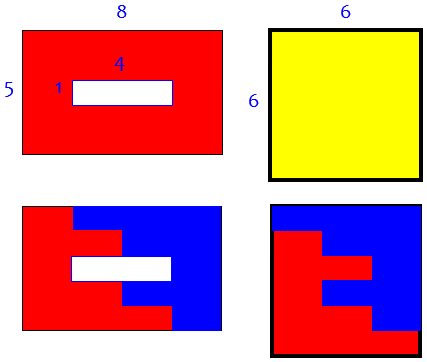
Now you try the same ideas on the 10-by-10 room and 9-by-12 carpet with a 1-by-8 hole in the middle.
Of course, we’ve seen the solution already!

Pingback: Disappearing Area? – The Math Doctors