A Geometrical Limit

(A new question of the week)

We usually see limits applied to functions in a calculus class. An interesting question from late October deals with a limit in a geometrical construction based on a function. We’ll be seeing how to discover a proof, then several alternative proofs, and finally what the answer means.

Limit of the y-intercept

Here is the initial question:

Hello, I am currently in my college holidays and I have decided to do some maths to improve. My weakness is graphing and I am hoping to get some help or the solution on this question.

Question:

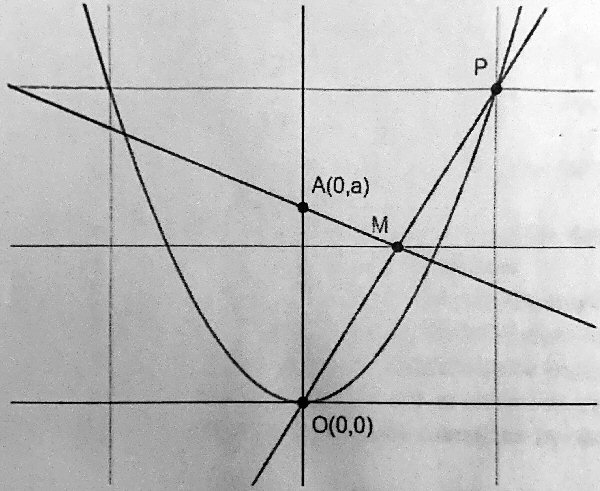
Let P(k, k^2) be a point on the parabola y = x^2 with k > 0.
Let O denote the origin.
Let A(0, a) denote the y-intercept of the perpendicular bisector of the segment OP.

What is the limit of a as P approaches O?

Thank you!!

The graph provided isn’t quite to scale (the two lines don’t look quite perpendicular), but you can try to imagine, as P moves toward O, what might happen to A. Would it just keep moving up toward infinity as AM gets steeper, or would it approach some particular point on the y-axis? Not obvious, is it?

Jalal had submitted the question under the category Geometry, though it involves an algebraic equation, and he specifically mentioned graphing; the limit concept is from calculus, and Jalal’s reported age range suggested the beginning of college. So I couldn’t be sure what approach to suggest.

Having explored the problem enough to find a solution, I answered:

Hi, Jalal.

This is an interesting problem, and is about a lot more than mere graphing!

Here’s how I’d start:

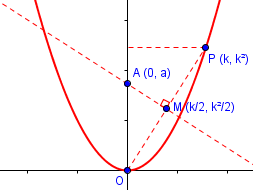
On the picture, label the coordinates of point P, and of M, the midpoint of OP. Then you might think about the slope of AM and how it relates to that of OP. There are several ways you can use this to find the value of a as a function of k; you could write the equation of line AM, or you could use similar triangles, or the slope formula. How you do that is up to you; so I’d like to see what you can do with the problem in order to see how best to help.

I’ll also want to know what you have learned about limits, since that is a topic beyond geometry. (But the limit involved here is an easy one.)

I look forward to hearing more from you!

We’ll eventually be looking at all three of the methods I suggested.

Jalal wrote back:

I haven’t learned much limits but I have learned about gradients, differentiating normal line and tangents.

Thank you

So he knew a little calculus; all we need of it here will be the mere concept of a limit.

Starting the work

I replied:

This doesn’t require any calculus, just analytic geometry, and in particular the relationship between slopes (gradients) of perpendicular lines. If you use the similar triangle approach I suggested as an alternative, you don’t even need that. (The limit is very simple.)

Here is the first step I suggested, with coordinates of P and M labeled:

Please show what work you have done, using any method, so I can see where you need help.

The coordinates of P come from the equation of the parabola; those of M come from the midpoint formula, averaging the coordinates of the endpoints.

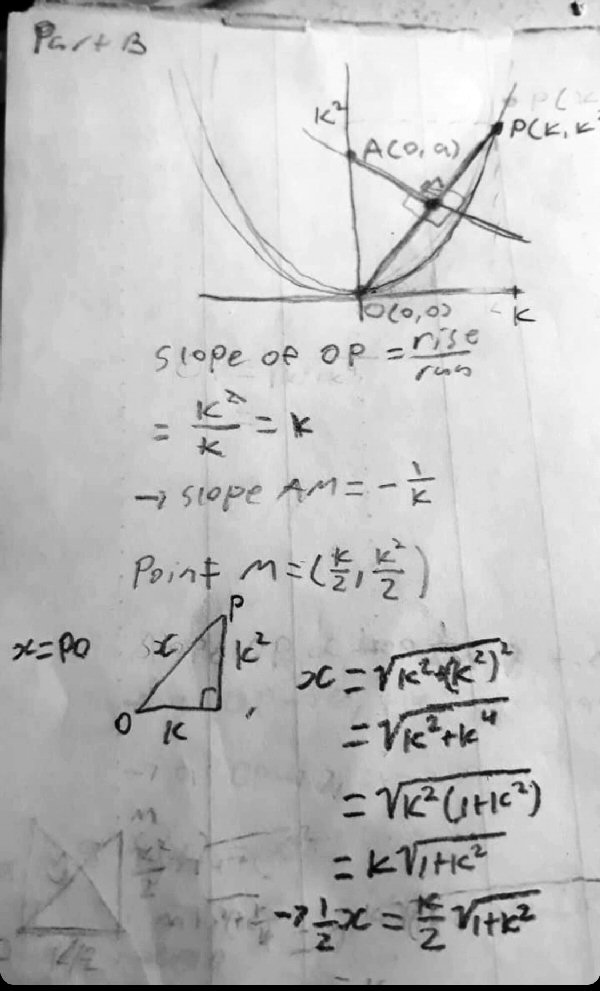
Jalal now showed work:

I will show you what I have done before you sent me the last message.

Jalal has correctly found the slopes, but has not dealt with A yet. The last half finds the lengths of OP and then OM, which he won’t actually be using – but we’ll see it at the end when I show another method.

I answered:

I don’t think you need to find the distance OP. But you have the slope of AM and the coordinates of M; can you write an equation for the line AM?

A first draft

Jalal took a slightly different approach than I had in mind, writing equations for two lines and intersecting them.

OP = kx

AM = (-1/k)x + a

kx = (-1/x)x + a

k²x – -x + ka
x(k²+1) = ka
Sub k/2 into x and @ M, x = k/2

k/2(k² + 1) – ka
k(k² + 1) = 2ka
k² + 1 = 2a

Therefore, a = k² + 1/2
a = k²/2 + 1/2

k –> 0, OP–>0, AM –> infinity

Lim a = lim (1/2(1 + k²)) = 1/2
k–>0   p–>0

The approach Jalal chose was to find the equations of line OP and of line AM (given its y-intercept A), and using the fact that that intersection is M. The answer was right, but the work was hard to follow and had a few errors in detail.

Cleaning it up

I approved, and fixed up minor details in the work:

You got it!

I’ll make a couple comments on your work, and then show my approach, which was a little different.

Your work:

OP = kx               <— I think you meant that line OP has equation y = kx.

AM = (-1/k)x + a <— Similarly, line AM has equation y = (-1/k)x + a.

kx = (-1/k)x + a   <— Finding the intersection, which should be point M; I’ve corrected a typo.

k²x = -x + ka       <— You multiplied by k; I’ve corrected a typo.
x(k²+1) = ka
Sub k/2 into x and @ M, x = k/2 <— Now you use the fact that this point is M.

k/2(k² + 1) = ka   <— I’ve corrected a typo.
k(k² + 1) = 2ka
k² + 1 = 2a

Therefore, a = (k² + 1)/2 <— You omitted these parentheses.
a = k²/2 + 1/2      <— Good.

k –> 0, OP –> 0, AM  –> infinity <— Line OP approaches line y=0, and AM becomes vertical ??

Lim a = lim (1/2(1 + k²)) = 1/2    <— Good.
k–>0   p–>0

The part about OP–>0, AM –> infinity isn’t needed, fortunately. All you need is what you did at the end, that a approaches 1/2.

The only actual errors were mere typos.

A different way to do the same thing

I then showed the method I’d referred to as “using the slope formula”:

Here’s what I did, which is essentially the same thing turned inside-out:

Slope of OP is k, so slope of AM has to be the negative reciprocal, -1/k.

Slope of AM is Δy/Δx = (k²/2 – a)/(k/2) = k – 2a/k.

Setting these equal, k – 2a/k = -1/k.

Multiplying by k, k² – 2a = -1.

Solving for a, a = (k² + 1)/2.

As P approaches O, k approaches 0, a approaches 1/2.

Your work, with my little corrections, is as good as mine.

I hope you enjoyed that!

We both obtained the equation \(a=\frac{k^2+1}{2}\) for the y-intercept as a function of k. [Jalal, if you are reading this, I discovered a sign error in what I actually wrote to you, which I have fixed here! I hope that didn’t confuse you.]

In the course of the work, the derivation was invalid when \(k=0\), but valid otherwise; the equation we ended up (multiplying by k) with removes that discontinuity, so we just have to set \(a=0\) to get the answer. As a result, the concept of limit only shows up if you are reading carefully!

More alternative solutions

Let’s try a couple more ways to get the solution.

Point-slope equation

Probably when I suggested writing the equation of line AM, I had in mind using the point-slope method with point M. We know the slope \(-\frac{1}{k}\) and the point M \(\left(\frac{k}{2},\frac{k^2}{2}\right)\), so the point-slope form $$y-y_0=m(x-x_0)$$ becomes $$y-\frac{k^2}{2}=-\frac{1}{k}\left(x-\frac{k}{2}\right)$$ Putting this into slope-intercept form by expanding and solving for y, we get $$y=-\frac{1}{k}x+\frac{1}{2}+\frac{k^2}{2}$$ Therefore the y-intercept is $$a=\frac{1}{2}+\frac{k^2}{2}$$

This is the same formula we got above, and the limit is again \(\frac{1}{2}\).

Similar triangles

The yellow (AMO) and green (OXP) triangles here are similar, because each side is perpendicular to the corresponding side of the other.

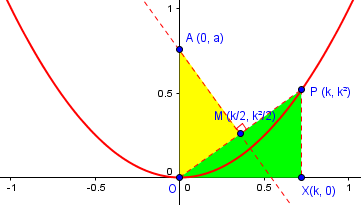
This gives us the proportion $$\frac{\text{OA}}{\text{OM}}=\frac{\text{PO}}{\text{PX}}$$ so that $$\frac{a}{\frac{1}{2}\sqrt{k^2+k^4}}=\frac{\sqrt{k^2+k^4}}{k^2}$$ Solving for a, $$a=\frac{k^2+k^4}{2k^2}=\frac{1+k^2}{2}$$ which again is the same formula.

Behind the scenes

Let’s take a look at what’s happening. Here is a graph of the problem showing P closer to A than in my image above; I have superimposed on the figure the graph (in green) of our function \(a=\frac{k^2+1)}{2}\), so you can see how it approaches \(\frac{1}{2}\):

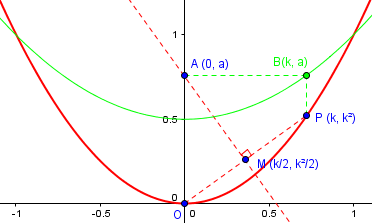
For instance, the point B on the green curve directly above P is directly to the right of A. As P moves toward O, A moves down to \(\frac{1}{2}\), the vertex of the parabola \(y=\frac{x^2+1)}{2}\). 

In the next picture,I have moved P even closer to O, and added a circle centered at the limit point \(\left(0,\frac{1}{2}\right)\). This is called the osculating circle to the parabola at the vertex:

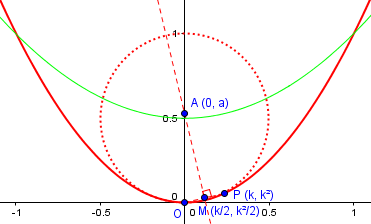
The osculating circle touches the parabola as closely as possible for as long as possible (“osculate” is Latin for “kiss”); its radius is called the radius of curvature of the parabola, and its center, our limit point, is called the center of curvature. You can see why, with P nearly on this circle, the perpendicular would nearly pass through that center.