For the next couple weeks, we’ll look at a few “dissection problems”, which involve cutting a shape in various ways. Here, we look at what turns out to be a simple problem, though it seems at first that it would be complicated: dividing a cake into pieces with the same amount of cake and the same amount of frosting. I’ll start with a couple answers that gave only hints, and work up to full solutions, so you can discover it at your own pace.
Equal volumes
We’ll start with this question from 2001:
Five Equal Pieces of a Square Cake Ravina has a square birthday cake. Its side length is 20cm. She wishes to cut the cake into five pieces, one for each of her four friends and one for herself. She wants to use straight vertical cuts to make five pieces of equal volume. Suppose that Ravina makes the first cut from the cake's center to a point from the top left corner. Where must she make the other four cuts if they all start for the cake's center? I haven't even started... I would not even know where to start. Please help me!
We’ll be seeing several variants of the problem, of which this is relatively simple: We are told how big the square is (but not the cake’s height), and want to cut it into 5 equal parts. But rather than make 4 cuts parallel to the side, as we would expect (especially if two people want most of the icing!), we are required to make wedges that meet at the center:
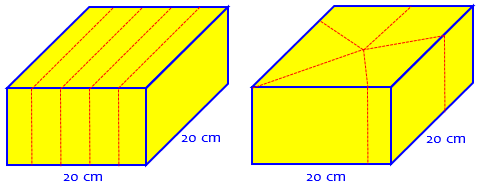
Because the cuts are made vertically, it doesn’t matter how tall the cake is; the volume of each piece is proportional to the area on top. The only question is, how do we find the right locations?
I answered briefly, just offering a hint:
Hi, Katie.
A good place to start is to think about what the area will be for any wedge cut from the cake, like this:
+-----------+
| |
| |
| + |
| / \ |
| / \ |
+--------+--+
|<---d-->|
Once you've done that, think about the area of a wedge that goes around a corner, like this:
+-----------+
| |
| |
| + |
| / \ |
| / + --
+-----------+ ^
|<-------d-----+
You will find that the distance d along the outside is all you need to know, and using that you can find the correct value of d for which each piece is 1/5 of the cake. The answer is surprisingly simple!
The area of the triangular piece can be found by the formula \(A = \frac{1}{2}bh = \frac{1}{2}d\cdot 10 = 5d\). The area of a wrap-around piece can be thought of as the sum of two triangles. I’ll let you think about the rest for now.
Equal volume and area!
Two months later, we got a similar question with an additional requirement:
Dividing a Square Cake into Five Equal Pieces How can you divide a square-topped cake that is a rectangular solid and is frosted on all faces into five pieces so that everyone receives the same amount of cake and icing? All cuts must be perpendicular to the surface. I can not figure this out. All I can do is divide the cake four ways and eight ways. Please help me or tell me a way that I can try to solve this problem.
We still need vertical cuts, which prevents some trickery; but now we need to make both the volume (cake) and the amount of surface area (icing) the same for each piece. That seems like a much bigger challenge. Pam has presumably used symmetry to make 4 or 8 pieces that are all congruent, and therefore have the same volume and area:
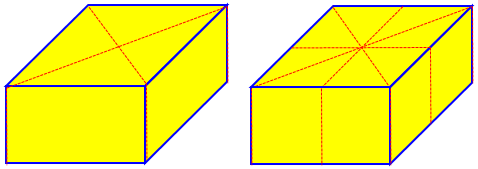
But you can’t do that with five pieces, can you?
I answered again, with more or less the same hint:
Hi, Pam.
This problem is easier to solve than you would think. I suggest you start by thinking about wedge-shape pieces like this:
s
+---------------+
| |
| |
| |
| + |
| / \ |
| / \ |
| / \ |
+---+-------+---+
a
Then you can extend it to wedges that wrap around a corner like this:
s
+---------------+
| |
| |
| |
| + |
| / \ |
| / +
| / |b
+---+-----------+
a
You can find this area by drawing the line from the center to the corner to divide it into two triangles, and finding the area of each triangle.
Once you've done this, I think you will have a good idea what to do.
Let’s take it a little further this time. Here we weren’t given specific lengths, so a general description is all that is expected; but let’s keep the side lengths at 20 cm from the first problem. We saw that the area of a triangular piece is \(5a\), using the variable we have here; the area of the quadrilateral piece is \(5a + 5b = 5(a+b)\), still 5 times the amount of perimeter used by the piece (the d in my first answer). This is the key idea.
Now we want to divide the area of the top of the cake, \(20\times 20 = 400\text{ cm}^2\), into 5 equal parts, so each has to be \(80\text{ cm}^2\). Setting \(5d=80\), we find that the distance along the side has to be 16 cm. And since each piece will have the same distance along the perimeter, they will not only have the same area of icing on top, but also around the side.
The answer, with details
At the end of that answer, I referred to the following answer, from 1999, which we can look at now:
Cutting a Square into Five Equal Pieces Hi Dr. Math, I was wondering how it is possible to divide a square cake into five equal parts. There are some restrictions: you cannot divide the cake into ten parts and give two to each person, and it must be cut through the center point. ___________ | | | | | . | | | | | ----------- What I have done is these but they were rejected. ___________ ___________ | | | | | | | _|__ | | \ | / | |---| |--- & | \|/ | | |__| | | / \ | | | | | / \ | --------- --------- Can you help me please? Thank you, Doctor.
The first attempt doesn’t use the center; but the second is just what was described – if the measurements are right.
Note that we are back to a question that doesn’t worry about the icing, though the answer will.
Doctor Rob answered:
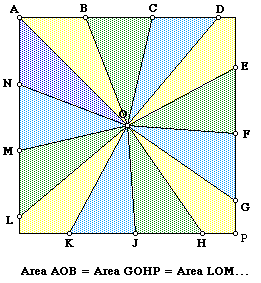
Thanks for writing to Ask Dr. Math. Your last drawing above contains the right idea. Measure the length of the sides of the square, which is the base of the cake. Call that s. The perimeter of the square is then 4s. Divide that by 5. Now from any starting point (such as the center of the top edge in your picture), measure around the edge a total distance of 4s/5. Mark this point, and measure around the edge again a total distance of 4s/5. Repeat this until you return to the starting point. Now from the center, make cuts to all five points marked. That will divide the cake into five equal volume pieces, and furthermore, each piece will have the same amount of icing, too.
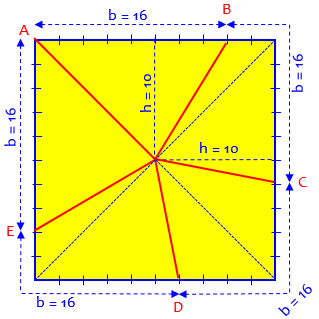
Here’s what this looks like when \(s=20\) as in the first question:
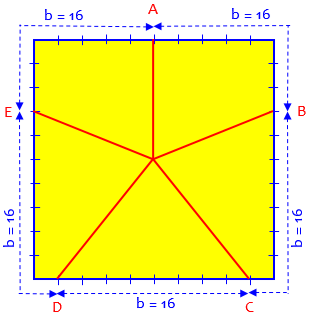
Here the perimeter is 80, so we moved \(\frac{1}{5}\) of that distance from one point to the next, that is, \(\frac{4}{5}\) of 20 = 16. I marked each side in tenths (2 cm).
So that’s the answer. But is it true?
To prove that the volumes of the pieces are all the same, it is enough to prove that the areas of the four quadrilaterals and one triangle are all the same. Draw the diagonals of the square. That will cut the quadrilaterals into two triangles each. All the nine triangles will have height s/2, and their bases will be s/2, 3s/10, 7s/10, s/10, or 4s/5. Starting at the starting point and moving around the perimeter of the square, you'll see that
s/2 + 3s/10 = 4s/5
7s/10 + s/10 = 4s/5
4s/5 = 4s/5
s/10 + 7s/10 = 4s/5
3s/10 + s/2 = 4s/5
In our example, the individual bases are, respectively, \(AB = 10 + 6\), \(BC = 14 + 2\), \(CD = 16\), \(DE = 2 + 14\), and \(EA = 6 + 10\), all equal to 16 cm.
Starting at one corner and moving around the perimeter of the square, you'll see that
s/2 + s/2 = s
3s/10 + 7s/10 = s
s/10 + 4s/5 + s/10 = s
7s/10 + 3s/10 = s
Each side adds up to \(s = 20\). Here we see the 5 pieces split into 9 triangles, along with the fact that they all have the same altitude.
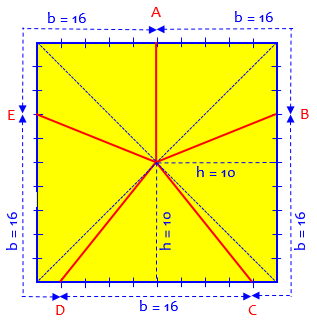
For each triangle, the area is \(A = \frac{1}{2}bh = \frac{1}{2}b\cdot \frac{1}{2}s = \frac{1}{4}bs\).
Thus the triangle areas will be s^2/8, 3s^2/40, 7s^2/40, s^2/40, or s^2/5.
When you add up the areas of the triangles to get the areas of the quadrilaterals, all quadrilaterals will have area s^2/5, or 1/5 of the total area of the square:
s^2/8 + 3s^2/40 = s^2/5
7s^2/40 + s^2/40 = s^2/5
s^2/5 = s^2/5
s^2/40 + 7s^2/40 = s^2/5
3s^2/40 + s^2/8 = s^2/5
Now the volume is the area of any of these polygons times the height of the cake, so all volumes are equal to hs^2/5, and all icing areas are equal to (4h+s)s/5.
Each piece has a volume equal to its area times the height h of the cake, so they are all equal, \(\frac{1}{5}s^2\); and the icing on each piece is its top area plus the area of a rectangle with width \(\frac{4}{5}s\) and height h.
Notice that if you had started at, say, a corner point, the quadrilaterals would be different shapes, but the area of each would still be s^2/5, because the triangles forming them have common altitude s/2 and the sum of their bases is 4s/5, so the total area is
A1 + A2 = ab1/2 + ab2/2
= a(b1+b2)/2
= (s/2)(4s/5)/2
= s^2/5
For the same reason, any starting point could have been used.
Here is a cake with the first cut at a corner:
How about 13 pieces?
Now, it’s curious that all these questions were about five pieces; we’ve had a couple with different numbers, too. What if there were 13? Consider this question from Jim, in 1998:
Dividing A Cake - A Math Puzzle You have a nine-inch-square cake. It is a two-layer cake. Each layer is one and one-half inches high. Each layer is covered with 1/4-inch-thick frosting and so are the sides. There is no frosting on the bottom. Using straight knife cuts, how can you divide the cake into 13 pieces so that each piece has exactly the same amount of cake and frosting? After pieces are cut they may be put back together, but you may not remove any cake or frosting.
This is the most detailed version of the problem we have, with complete dimensions, and the requirement that both cake and frosting (also called icing) be divided equally. We don’t really need any of the dimensions, though we’ll see a little issue with the thickness of the frosting.
Doctor Wilkinson answered:
This is a very nice puzzle. In case you want to work on it a little longer on your own, I'll give you a couple of hints. If you get stuck or you just want the answer, let me know. 13 is too big; it's hard to visualize the problem with such a large number of pieces. Try some smaller number like 5 (4 or 2 would be too easy). If the cake were circular instead of square, it would certainly be easy. You would just mark off points on the circumference that would divide it into 5 equal parts, and cut from the center of the circle to these points, right? Now see if you can do something similar with a square cake.
“Try a smaller number” is a standard piece of advice when you face a big problem. Can you see why 5 is the best choice?
“Try a simpler but similar problem” is also standard; thinking “what if it were round?” can lead to the idea of dividing the perimeter equally, though one might not at first think it could work.
Jim replied, wanting more than just a hint (without directly saying that he really needs more than the hint!):
Thank you very much for your response. These hints are very helpful. I think that I know how to go about solving the problem, but could you please send me an explained solution?
Doctor Wilkinson responded:
The hint I gave you was really a very good one. You just need to be bold and follow it exactly. If you divide the circumference of the cake into 13 equal parts and then make your cuts from the center of the cake to each of the 13 points on the circumference, all the pieces will have equal amounts of both cake and frosting! To see this, notice first that the amount of cake in a piece is just the area of the top of the piece times the thickness of the cake. The amount of frosting from the top is just the area of the top times the thickness of the frosting, and the amount of frosting from the side is just the length of the part of the piece on the edge of the cake times the thickness of the cake times the thickness of the frosting. Now if you divide the circumference into 13 equal parts, you've taken care of the frosting on the side, and you just need to be sure that the pieces have equal area to take care of the cake and the frosting on the top.
There’s one little issue with the thickness of the frosting: we are cutting through the frosting at an angle, so the parts on the sides are not exactly rectangular, and therefore not quite proportional to their width. You can see the issue here:
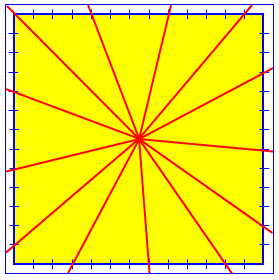
Pieces closer to the center have a wider angle, making trapezoids with a little more area. But the standard puzzle assumes the icing is very thin (perhaps just a glaze), minimizing this problem!
There are two kinds of pieces of cake if you divide it as I suggested: triangular wedges, and pieces that go around a corner of the cake. For the triangular pieces, the area is one half the base times the height. The height is just the distance from the center of the cake to the edge, which is the same for all the pieces, and the base is one of those equal divisions of the circumference, so that's the same for all the triangular pieces also. I'll let you think about the case of the around-the-corner pieces, but they work too. Here's a picture:
What about the angles?
We’ll close with a question about only 3 pieces; by now you know what to do, but what if you had to identify the angles for the cuts? This question is from 2001 again:
Dividing a Square in Thirds I want to take a square and divide it into three equal pieces using three lines radiating from the center of the square. I determined that each line has to have an angle of 120 degrees to complete a circle. The difficulty is in getting the areas of the square to be equal.
This one is not posed in terms of a cake, and doesn’t mention the equivalent of icing; Frank is apparently thinking of the fact that three sectors of a circle with central angles of 120° will be equal. What would the angles be for a square?
Doctor Rob answered, starting with the same idea we’ve already seen several times, and then calculating the angles. For simplicity, he uses a coordinate system and makes each side 2 units long:
Thanks for writing to Ask Dr. Math, Frank.
There is more than one way to do this. Here are two:
A(-1,1) G B(1,1)
o-----------+-----------o
| -_ . |
| -_ . |
| -_ . _,o E
| -_ . _,-' |
| -_. _,-' |
H + - - - - - o - - - - - + I
| /.O |
| / . |
| / . |
| / . |
| / . |
o-----o-----+-----------o
D(-1,-1) F J C(1,-1)
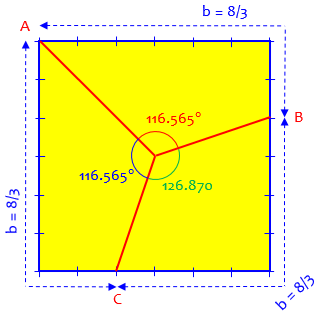
The first way is to make one line from A to O. Then the area of AGO and AHO are both 1/2 square unit. That means the area of GBEO and HDFO both have to be 5/6 square unit to make a total of 4/3 square unit for ABEO and ADFO. That leaves OEI and OFJ with an area of 1/6 square unit, so E must have coordinates (1,1/3) and F(-1/3,-1). Then:
<AOF = <EOA = arccos(-1/sqrt[5]) = 116.565 degrees
<FOE = arccos(-3/5) = 126.870 degrees
These angles can be found by using the Law of Cosines and the lengths of the sides of the triangles AOE and EOF.
Using the technique we’ve seen already, with a total perimeter of 8, we need \(AB + BE = \frac{8}{3}\), so \(BE = \frac{8}{3} – 2 = \frac{2}{3}\), which confirms that \(E = (1, \frac{1}{3}\).
Let’s find one of those angles using the Law of Cosines: The sides in triangle AOE are $$|OA|=\sqrt{1^1+1^2}=\sqrt{2}\\ |OE|=\sqrt{1^2+\left(\frac{1}{3}\right)^2}=\sqrt{\frac{10}{9}}=\frac{\sqrt{10}}{3}\\|AE|=\sqrt{2^2+\left(\frac{2}{3}\right)^2}=\sqrt{\frac{40}{9}}=\frac{2\sqrt{10}}{3}$$ By the Law of Cosines, $$|AE|^2=|OA|^2+|OE|^2-2|OA||OE|\cos{\alpha}\\\cos{\alpha}=\frac{|OA|^2+|OE|^2-|AE|^2}{2|OA||OE|}=\frac{\left(\sqrt{2}\right)^2+\left(\frac{\sqrt{10}}{3}\right)^2-\left(\frac{2\sqrt{10}}{3}\right)^2}{2\sqrt{2}\frac{\sqrt{10}}{3}}\\=\frac{2+\frac{10}{9}-\frac{40}{9}}{\frac{4\sqrt{5}}{3}}=\frac{-12}{12\sqrt{5}}=-\frac{1}{\sqrt{5}}$$
The rest, of course, are similar.
Here is an accurate picture (sides marked in thirds):
Starting vertically, we get different angles:
A(-1,1) G B(1,1)
o-----------+-----------o
| . |
| . |
F o._ . _,o E
| `-._ . _,-' |
| `-._ . _,-' |
H + - - - - - o - - - - - + I
| |O |
| | |
| | |
| | |
| | |
o-----------+-----------o
D(-1,-1) J C(1,-1)
The second way is to put one line from J to O. Then the areas of OIE and OHF must be 1/3 unit, so the coordinates of E and F are E(1,2/3) and F(-1,2/3). Then the angles are:
<JOE = <FOJ = arccos(-2/sqrt[13]) = 123.690 degrees
<EOF = arccos(-5/13) = 112.620 degrees
These angles can be found by using the Law of Cosines and the lengths of the sides of the triangles JOE and EOF.
Here is the picture:
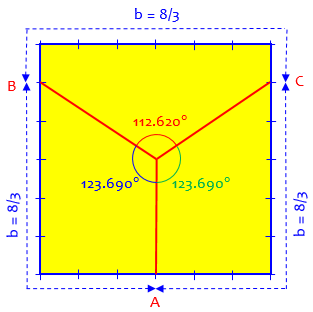
It’s easier, of course, just to measure around the perimeter; but it’s worth seeing how the angles differ from the 120° of a circle.

Pingback: Cutting and Rearranging a Rectangle – The Math Doctors