(A new question of the week)
Sometimes we have lots of quick questions and a number of long discussions, neither of which seems suitable for a post. This time I’ve chosen to combine two distantly related questions, one recent and one from several months ago, both involving tangent lines to functions.
Question 1: How can a line have a tangent?
The first is from Akhtar, in mid-October:
Hi Dear sir,
I want to gain some important knowledge about the following question.
Find the equation of tangent line to the graph of f(x) = 3x – 7 at (3, 2).
We find equation of tangent by y – y1 = m(x – x1) using this we get y = 3x – 7 (same to given line).
Because every straight line is its own tangent. Thus we get the same equation.
But graphically if we draw the line and then draw tangent to it which will coincide with the line.
So both lines touch at infinitely many points, so how it remains tangent?
Please discuss and remove my confusion.
Best regards
Normally, when we find a tangent line to a curve, it looks something like this:
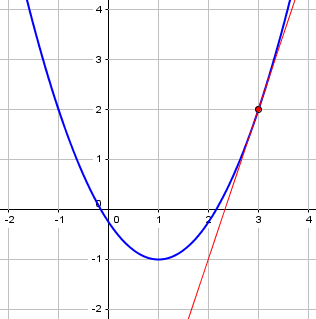
The tangent line just touches the curve at one point. (In fact, that’s what “tangent” means in Latin: “touching”.) But in this problem, the “curve” is the line!
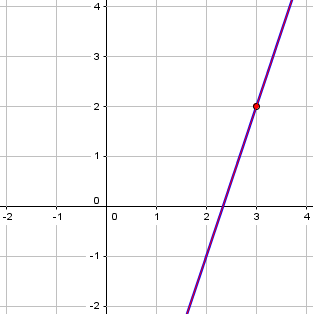
How can we call that a tangent?
What a tangent isn’t
Doctor Fenton answered:
I think the issue here is what the meaning of a tangent line is. On my first day in a calculus class, the professor asked that question: What is a tangent line to a curve? Someone offered a common description: a line which touches the curve at only one point. The professor then drew a curve like y = x2, and the vertical line x = 0, which does touch the curve at only one point, the origin. But this vertical line is not our intuitive concept of a tangent line, while the horizontal line y = 0 fits our intuitive idea (and is the correct tangent).
This first attempt is, in fact, used as a definition of a tangent line to a circle in geometry; there, it makes sense. But in calculus, we are talking about all sorts of curves, and that definition doesn’t work any more.
Here is what the professor might have drawn:
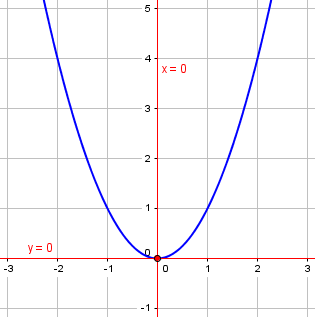
Both red lines intersect the curve in only one place, but we’d never call the vertical line a tangent.
Then someone offered a modification, saying that the line must not cross the curve. Then the professor drew a curve like y = x3, and the line like y = 0 (the x-axis), which of course is the correct tangent line – but it does cross the curve!
Here is what he drew:
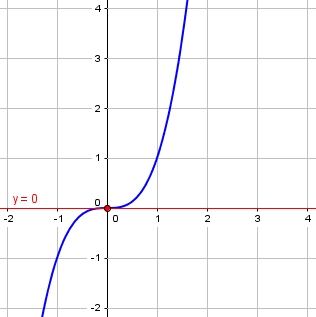
Now, he could also have drawn this:
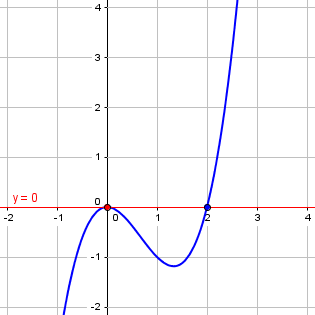
This time, the line doesn’t cross the curve at the point of tangency; but it crosses elsewhere.
So, the definition of “tangent line” can’t be merely that it intersects in only one place, because that can be true of non-tangent lines, and also can be false of tangent lines. And it can’t be that it intersects without crossing, because that can be false of a tangent line.
(Incidentally, some of these ideas are touched upon (no pun intended) in the post Tangents Without Calculus.)
So how can we define “tangent” to fit our intuition?
What a tangent is
I don’t recall if any other modifications were offered, but the point is that the only definition of a tangent line which does yield our intuitive concept is that the tangent line to a curve y = f(x) at a point (a, f(a)) on the curve passes through the point (a, f(a)), and has the slope m = lim(x→a) [(f(x) – f(a))/(x – a)].
This is the calculus definition: The tangent line is simply the line through the given point whose slope equals the derivative of the curve, which in turn is defined as a limit. One important thing about this approach is that it is a local concept: It focuses on what is happening to the curve near the point of interest, not far away (e.g. whether the line intersects the curve somewhere else). In effect, the tangent line (solid red) is the limit of secant lines (broken red) passing through the point, as the other point (blue) approaches the point of tangency:
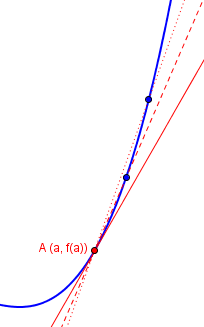
Geometrically, the idea is that the tangent line is the “best” straight line approximation to the curve y = f(x) at the point (a, f(a)). Any line passing through this point has the form y = m(x – a) + f(a). If two lines both pass through (a, f(a)), y = L1(x) = m1(x – a) + f(a) and y = L2(x) = m2(x – a) + f(a), then the difference between the two lines at x is d = (m1 – m2)(x – a). The size of this difference at a point (x, f(x)) some distance away from (a, f(a)), relative to the displacement (x – a), is |(m1 – m2)(x – a)|/|x – a|, which is a constant |m1 – m2|.
That is, the distance d between two lines decreases linearly as we approach their common point, so the ratio of that distance to the horizontal distance is a constant equal to the difference in their slopes:
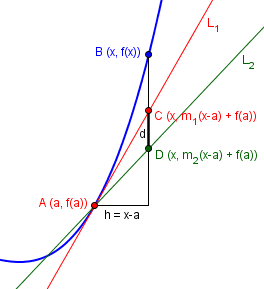
The red line is the tangent L1, and we can see that hugs the curve more tightly the closer we get to A:
So if the slope m1 is defined by the limit
m1 = lim(x→a) [(f(x) – f(a))/(x – a)] ,
then
lim(x→a) [f(x) – L1(x)]/(x – a) = lim(x→a) [f(x) – (m1(x – a) + f(a))]/(x – a)
= lim(x→a) [{f(x) – f(a)} – m1(x – a)]/(x – a)
= lim(x→a) [{f(x) – f(a)}/(x – a)] – m1
= 0.
Here we are looking at the the distance from L1 to the curve; this time, the ratio is not a constant, but decreases to zero. This implies a “close fit”. What about other lines?
For any line L2(x) = m2(x – a) + f(a) with m2 ≠ m1, the difference [(f(x) – L2(x)]/(x – a) can be written as
[f(x) – L2(x)]/(x – a) = [f(x) – L1(x)]/(x – a) + (L1(x) – L2(x)]/(x – a)
so that
lim(x→a) [f(x) – L2(x)]/(x – a) = m1 – m2 .
There is only one slope m for which this limit is 0: m1. That’s why there is only one tangent line.
Only the one line at the proper slope allows this ratio to approach zero.
This is relevant in higher levels of calculus:
This is also the idea that has to be used to define the derivative (not just the partial derivatives!) of a function of more than one variable. It is sometimes called the “total differential” of the function f(x, y) at a point (a, b): the linear function L(x, y) = Ax + By such that
lim((x, y)→(a, b)) [{f(x, y) – f(a, b)} – L(x, y)]/||x – y|| = 0 .
Does this help?
That last bit was likely beyond Akhtar’s current needs, but the whole idea – that the tangent line is the “closest fit” line at a given point – is essential. Calculus is essentially a way to define what we mean by that.
Question 2: Tangent at the inflection point
The other question I want to look at came from Amia in mid-July:
Hi Dr Math
I want to check the solution of this problem, and your opinion about if the inflection point is extra information, not needed to solve the question, and what shall I think to find first, the tangent point or c?
The strategy for solving the question?
Thank you
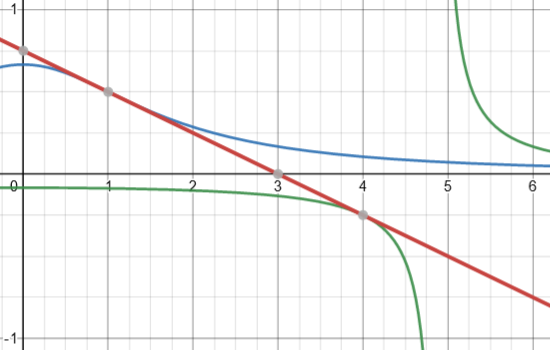
Here we are given a line and need to find a curve, within a family of curves, to which it is tangent at an inflection point. This does sound like there might be too much information; commonly, if you had a family of curves (e.g. \(y = x^2 + c\), you would expect just one of these curves to have a given line as a tangent at all:
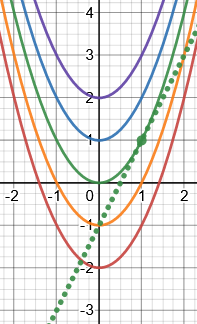
The spectrum of curves are for \( c=-2,-1,0,1,2\), and \(c=0\) gives the curve tangent to the line shown.
Our family of curves are a little different:
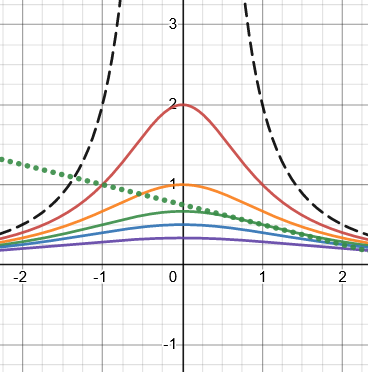
The dashed line is for \(c=0\), and the spectrum shows \(c=1,2,3,4,6\). (We’ll be looking at negative values for c later, when I expand the problem.)
Of course, we can’t just draw these graphs to solve the problem; but it does look like only one such graph is tangent to the line, and it just happens to be at an inflection point.
Amia’s work is good. He made a system of equations representing that the given line passes through a point \((x, f_c(x))\), and is tangent to the curve at that point: $$\left\{\begin{matrix}\frac{3-x}{4}=\frac{2}{x^2+c}\\ -\frac{1}{4}=\frac{-4x}{(x^2+c)^2}\end{matrix}\right.$$ He solved for both variables by solving the first equation for \(x^2+c\), which had the effect of eliminating \(c\), and finding two possible values for \(x\), namely 1 and 4; then finding two possible values for \(c\) in each case. Only one of these fit the requirement that \(c>0\).
Amia’s question about whether to find the point or the parameter first is moot; he really found them both together as a solution of the system. But the question about the inflection point is interesting, and the extraneous solutions made me curious to dig deeper.
Is there extraneous information?
I answered, having tried solving it algebraically with a twist:
Hi, Amia.
First, you’re right that the problem can be solved without using all the information; but since the problem requires that the point of tangency be an inflection point, you must check that it is. You can’t ignore a condition in the problem!
In other words, Amia just found c such that the given line is a tangent to the curve, but now needs to verify that the point of tangency is a point of inflection. Without that check, we might (conceivably) get an invalid solution. We can see from the green graph above that his solution does pass this test visually; to test it algebraically, we observe that the second derivative is $$f ”(x)=\frac{4(3x^2-c)}{(x^2+c)^3}$$ which is zero at \(x=\pm\sqrt{\frac{c}{3}}\). For Amia’s solution, \(c=3\), this is \(x=\pm 1\), one of which is his point of tangency. So he’s good.
Second, there is more to check besides that. In your final steps, you appear to have rejected three of the possible values for c solely on the basis that they are negative. But you only used the fact that y’ must be the same on the line and the curve, not that y must be the same. If we ignore the (unnecessary, as it turns out) requirement that c > 0, and check all four values against f(x), we find that both c = 3 and c = -24 work, but c = -5 and c = -8 do not. Alternatively, if you used the equation of f to solve for c, you would get only c = 3 and c = -24 as solutions.
There are two issues here. The important one is that a tangent line must not only have the right slope, but also pass through a point on the line! Amia had used both criteria to form a system of equations and find x and c, but had not checked that both were satisfied. I checked all four possible solutions (\(x=1,c=3\), (\(x=1,c=-5\), (\(x=4,c=-8\), and (\(x=4,c=-24\), out of curiosity, and the last two weren’t really solutions even if we allowed negative values for c – they are extraneous solutions to the system of equations. We’ll see more about that momentarily.
So what do these four “solutions” actually represent? For that matter, what do the graphs look like if we allow c to be negative?
Not having graphed this family of functions, I was not yet aware how different the curves are for negative c. Here is what they look like, for \(c=-1,-2,-4,-8,-24\), as well as \(3\):
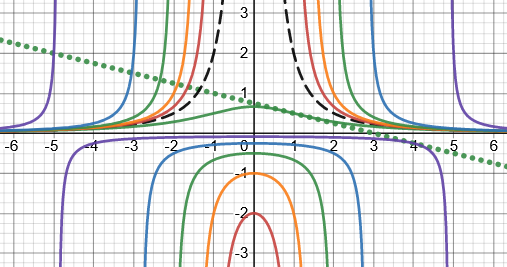
This shows both the real solution and the almost-solution: a point of tangency at \((4,-\frac{1}{4})\) with \(c=-24\), which is not an inflection point.
Exploring the extraneous solutions
Now I showed some of these details:
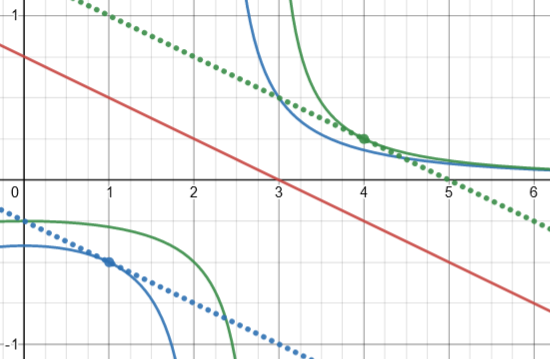
But then when you check the second derivative, you will find that for c = 3 the line is tangent at the point of inflection, while for c = -24 it is not. Here are graphs of those two cases (3 in blue, -24 in green), showing that the given line is tangent to both, but at different places (x = 1 and x = 4, respectively, the latter not being a point of inflection):
So we can still reject \(c=-24\), this time because it is tangent at a place other than the point of inflection (in fact, there is no POI for this curve).
But the other two points are rejected for a different reason:
Here are graphs of the other two non-solutions (c = -5 in blue, c = -8 in green):
I included the actual tangent lines (dotted) showing that these curves have the right slopes at x = 1 and x = 4, respectively, but have the wrong y (specifically, the wrong sign).
How did this happen? Looking back at Amia’s work, we see that in his equation (*”’) he squared the equation derived from the value of y, losing information about its sign. This is one of the usual reasons for extraneous solutions, and demonstrates why it was necessary to check that both equations were really satisfied.
So you got the right solution, but failed to check everything that needed to be checked, so you were lucky that you didn’t get an extraneous solution. If the problem had not specified c > 0, there would still be only one solution, but more ways you could get it wrong.
In fact, they could have dropped either the requirement that c be positive, or the requirement that the point of tangency be a point of inflection, and still get a unique solution; but if they dropped both, there would be two solutions.
Finding the inflection point first
I get the correct answer by doing the “obvious”, first finding the inflection point and either solving for x in terms of c or c in terms of x, then considering tangency at that point. Your method is “opportunistic”, using a shortcut you saw, which is a good idea and perhaps saved a little work, but that can sometimes be dangerous, too.
In any case, it’s an interesting problem.
Let’s close by solving the problem this way (still allowing c to be negative).
If we first find the inflection point, we find, as I did above, that possible locations are \(x=\pm\sqrt{\frac{c}{3}}\). This immediately eliminates negative values of c from contention!
Now, letting x have this value and seeking a tangent, we can find the curve with the desired slope at the inflection point by replacing x in the equation for the first derivative. We find that $$f'(x)=\frac{-4x}{(x^2+c)^2}=\frac{\mp 4\sqrt{\frac{c}{3}}}{(\frac{c}{3}+c)^2}=\mp\frac{3\sqrt{3}}{4c\sqrt{c}}$$ This is equal to the slope of the line, \(-\frac{1}{4}\), when \(c = 3\), and therefore \(x=1\). This is the solution we found before, with nothing extraneous.
But … we haven’t yet checked whether the line is actually tangent to the curve! Does it intersect the curve at \(x=1\)? Yes: The line has $$y=\frac{3-x}{4}=\frac{3-1}{4}=\frac{1}{2}$$ and the curve has $$y=\frac{2}{x^2+3}=\frac{2}{1^2+3}=\frac{1}{2}$$
So, just as in Amia’s solution, we had to do an extra check at the end to make sure our solution met all the requirements. That is typical of an overspecified problem.