(A new question of the week)
Here is an interesting little question about how drilling a hole affects volume and surface area. We’ll have one answer, and several explanations.
Volume decreases; does the area increase?
It came from Harkirat, in late October (as part of a discussion starting with a different question):
Hi.
I am trying to help my daughter with her studies. I’m not sure if I have solved this question correctly or not. Can someone check and confirm if I’ve solved it right or not:
My solution based on the logic:
Since cylinder is cut out from the centre, the volume of the solid left after taking out the cylinder will have lesser volume. So, volume will decrease.
Increase in surface area = CSA of cylinder = 2πrh = 2πr * 1 unit = 2πr
Decrease in surface area = 2 * Area of circle = 2 * πr^2 = 2πr^2
Intuitively, I feel 2πr > 2πr^2 => Surface area will increase.
So B is correct.
Is my reasoning correct?
Any help will be appreciated.
It’s obvious that the volume decreases, so some aspects of the problem seem silly. But there’s something tricky, and surprising, about the surface area! (I’ll ignore the fact that the picture doesn’t quite look right – the bottom of the hole shouldn’t be visible at this angle …)
Let’s take a moment to examine his work, which is good. How does the surface area change?
When we drill the hole,
we remove two circles from the top and bottom surfaces, and add the area of the sides of the hole (which is Harkirat’s CSA, “curved surface area”, which I would call the lateral surface area of the cylinder):
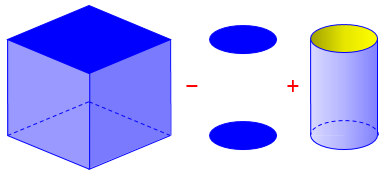
So the increase in area is \(2\pi r h – 2(\pi r^2)\), which, since the height \(h\) is 1, becomes \(2\pi r – 2\pi r^2 = 2\pi (r – r^2)\). Harkirat feels that this increase is positive. Is it?
First answer
Doctor Fenton answered with some questions:
Your work is correct, but it appears that you are looking for a justification that 2πr > 2πr2.
The circular cross section of the cylinder cut out of the cube fits within the square with side length 1, so what does that tell you about the diameter (and radius) of the cylinder?
As a general fact, if 0 < x < 1 (i.e. x is a positive number less than 1, then how does x compare with x2? (Remember that you can multiply an inequality a < b by a positive quantity c to obtain ac < bc, which is also a valid inequality.)
The idea he is implying is that we can multiply both sides of the inequality \(x<1\) by the positive number \(x\) to get the inequality \(x^2<x\), which leads to the required fact.
Second answer
Because of problems submitting that question, Harkirat had already submitted the same question a second time, with the more specific question,
Hi Friends.
Can someone look into my solution and help me understand how the surface area increases?
Thanks
Doctor Rick answered in that thread:
Hi, Harkirat.
I see that you submitted the same problem as a follow-up to another Math Doctor, and he may have some remarks in that thread, but I will give my perspective here.
You are correct that the volume of the new solid is less than that of the cube (which seems to be what they mean by “decrease”). And that leaves only one option, so unless we are allowed to choose none of the answers, it seems that we must choose that one.
So we can answer the problem with hardly any thought at all. But doing so is not very satisfying!
But is it true that the surface area increases? That’s the interesting question here. You thought it through, and decided correctly that the change in surface area is 2πr – 2πr2 (where r is the radius of the cylinder). Factoring out 2π, we have ΔS = 2π(r – r2). The question is now, is (r – r2) greater than or less than zero?
Your intuition is that r > r2, which would make the change in surface area ΔS positive — the surface area increases. I wonder where that intuition comes from? If I take a simple example — say, r = 3 — then r2 = 9, and r < r2. This is the intuition many students would have, I suspect — but not you!
There is, indeed, something else going on here. Why is my example inappropriate for this problem?
Probably the reason many people would think that \(r < r^2\) is that they are accustomed to squares of whole numbers. The square of 3, 9, is greater than 3 itself, for example. So we tend to think that squaring a number increases it. I am reminded of our post, How Can Multiplication Make It Smaller?.
Intuition and multiple perspectives
Harkirat wrote back, explaining his reasoning:
Hi Dr. Rick,
Thank you for your help.
Since the edge of the cube is given as 1 unit and the circular base is much smaller, it means that the radius of the circular base is in decimals, say 0.3 unit. Then r = 0.3 but r2 = (0.3)2 = 0.09.
Obviously, 0.09 is less than 0.3 and hence 2*pi*r > 2*pi*r2. That is what I thought was the reasoning behind this answer.
Am I correct?
This is good reasoning from an example, nicely focusing on numbers smaller than one, which is the key.
Doctor Rick responded with other ways to do the same thinking:
Yes, and we can do more than trying some examples (though that is enough to generate an intuitive feel for what’s happening).
Depending on what your child (or you) has learned about algebra, there are several algebraic ways we might consider the question of whether r – r2 is positive or negative. One thing we might do is to graph the function y = x – x2. (I just changed to variables that are more familiar in graphing — if you’re OK with it, we could stick with r.) Where does that graph go below the x axis?
Here is the graph:
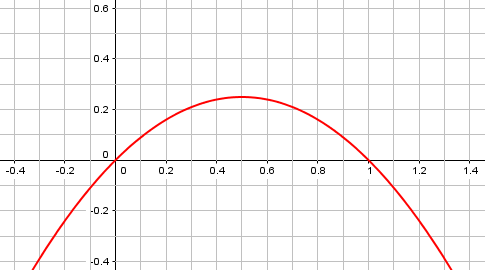
The function \(y=x-x^2=x(1-x)\) is a quadratic opening downward, equal to zero at \(x=0\) and \(x=1\), and therefore positive between them. We’re only interested in positive values of the radius, of course.
Apart from graphing, there are standard techniques for solving polynomial inequalities, which is another way of looking at what we have here: For what values of r is r – r2 < 0?
Such an inequality is often solved by locating the zeros of the function on a number line, and determining its sign in each region between those values (below 0, between 0 and 1, and greater than 1, in this case). That does, indeed, produce the same result as our graph. In fact, since this technique is often carried out by testing a value in each region, Harkirat’s own thinking is closely related: He tried “a decimal”, that is, a number between 0 and 1, namely 0.3, and found the difference to be positive.
Another approach: going back to graphing, you could graph the two functions y = x and y = x2. Where does the second graph fall below the first? That’s where x2 < x.
This is probably what first comes to my mind. Here is the graph:
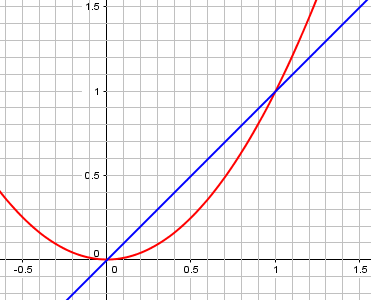
We can see that \(x^2\) is below \(x\) between 0 and 1, again.
The result of any of these investigations will be that x2 < x when 0 < x < 1. We can put algebra aside and think about it this way: When you square a number greater than 1, you get a greater number than you started with — because you’re multiplying the starting number by a number (the same number) that is greater than 1. When you square a positive number less than 1, you get a number less than you started with — because you multiplied the starting number by a number less than 1.
And in this problem, we know that r < 1/2.
This brings us back to the post on multiplication I referred to above: Multiplying by a (positive) number less than one decreases it. This, too, was probably on Harkirat’s mind. There is a lot of good intuition there!
Intuition and understanding
Harkirat had a further question:
Hi Rick,
Thank you for the detailed explanation. It makes sense.
However, the trouble is that this is an MCQ and hence has to be answered quickly and the child hasn’t got the time to go through the extra work. So, I’ll explain and show to her what you’ve suggested but to solve this I’ll give her the reasoning that I’ve gone with. So, she’ll have deeper understanding as well but will be able to solve such questions quickly too.
Thanks a ton!!
That is exactly right.
Doctor Rick answered,
That’s fine. There’s a place for teaching test taking strategies, as long as we don’t ignore opportunities to explore math more deeply.
As I said, if I had to choose fast, I would just choose B by process of elimination based on volume alone, and we don’t need to think about surface area at all. But if “MCQ” means “multi-correct question” rather than “multiple choice question”, and if “multi-correct” includes the possibility of “none correct”, then some further thought is needed, and what you did is reasonable.
There can be a lot of good thought behind a simple question. I suspect the question was not written as carefully as we have thought about it!
One more thing …
After writing this, it occurred to me that a question like this should not depend on the units used to measure the area; whether the surface is measured in square centimeters or in acres, drilling a hole should still increase the surface area. So the result is not dependent on the edges of the cube being 1 unit long. Therefore, the issue is not, ultimately, that the radius is a decimal. So let’s see what happens if we start with a 3-inch cube, or a 5-meter cube, or whatever.
Let’s say the side is \(s\) units, and the hole has radius \(r\) units:
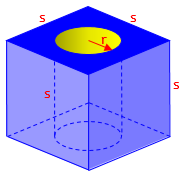
The whole cube has a surface area of \(6s^2\) square units. We remove two circles with a total area of \(2(\pi r^2)\) square units, and add a cylindrical surface of \(2\pi r s\) square units. The new area is $$6s^2+2\pi r s-2\pi r^2 = 6s^2+2\pi r (s-r)$$
Suddenly we can see the answer instantly: Since \(r<s\) (in fact, \(r<\frac{1}{2}s\)), the area is clearly increasing. And the reason is not really that \(r\) is a decimal, but that it is less than the side of the cube, which is also the height of the hole. (The \(r\) we worked with before was really the ratio of the radius to the side.)

