Ranges of Inverse Trig Functions

(Archive Question of the Week)

We have had a number of questions over the years about inverse trig functions and their ranges. For today’s question, I have chosen one from 2011, which will link to a number of others that I will not quote in detail.

Inverse sine, cosine, and tangent

Here is the question:

Arcsin, Arccos, Arcsec Are Confusing in their Ranges

Is the domain for arcsin 0 to pi? 

For arccos, is it -pi/2 to pi/2? 

I'm confused about how these are determined.

I think the domain of arcsin is 0 to pi because y is positive at these values. Is that the right reason?

Also, what is the domain of arcsec?

Jayson basically got everything wrong (from the word “domain” to the intervals he chose and the reason he gave), so I had to start from scratch; but I did so in part by referring to past answers that handled it well. As it turns out, I spent most of my time on the last line, and going beyond that. But here’s the start:

When you say "domain," you really mean "range," right? The restricted domain used for the secant, etc., before taking the inverse, becomes the range of the inverse function.

This range is not really "determined" as if we just have to study the function to find what its range MUST be. Rather, we make a partially arbitrary choice of a domain to which we can restrict the trig function -- a choice that will yield all possible values of the function exactly once, and be as well-behaved as possible. This is described here:

  Inverses of Trigonometric Functions
  http://mathforum.org/library/drmath/view/61051.html 

The general goal is to pick a range that is complete, contiguous (or as nearly so as possible), close to zero, and preferably positive rather than negative. For the sine, we can accomplish all but the last by using [-pi/2, pi/2], where sin(x) goes from -1 to 1. For the cosine, that wouldn't be one-to-one or give all possible values. But the next best choice, [0, pi], does meet all the goals. The tangent works the same as the sine, except that you can't include -pi/2 or pi/2.

In the reference, Doctor Rick explained why we need to restrict the domain of a trig function before making an inverse, and listed the usual choices. Since I can more easily include pictures than we could back then, let me add here a visual view.

Consider the sine and cosine first. In red below we see their graphs; neither is one-to-one until we choose some part of the graph, in blue. Each blue part has been chosen so that every possible value of y is present (what I called “complete” above) without repeating any, and the values of x are close to zero. Other choices are possible, but these are standard.

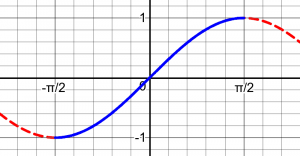
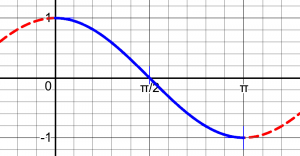
The inverse is found by interchanging the roles of x and y; the red parts would keep these from being functions, so we have chosen a range that makes it work:

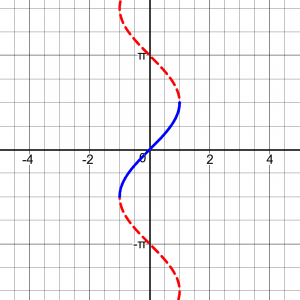
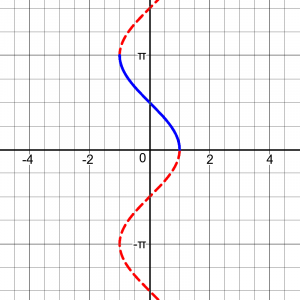
The tangent is much the same as the sine:

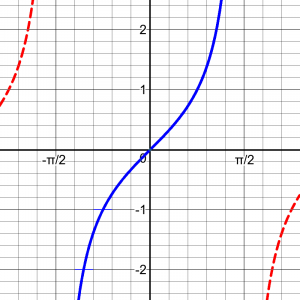
Inverse cotangent?

Let’s continue with my answer:

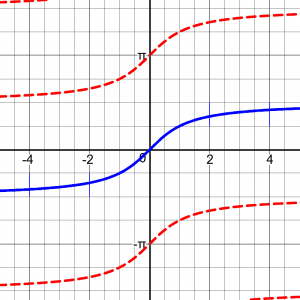
When you get to the cotangent, secant, and cosecant, the right choice is not quite as obvious. That's especially true of the cotangent. At first you'd think the cotangent should obviously have the same domain as the cosine (without the end points), much as we do for the tangent with regard to the sine; that makes its graph continuous, and that is the usual choice. But, as I said, nothing forces us to make that choice, and there are some reasons in favor of instead choosing (-pi/2,0) U (0,pi/2], even though that is not a contiguous interval. Here's a nice explanation I found (which happens to quote me!):

  http://www.squarecirclez.com/blog/which-is-the-correct-graph-of-arccot-x/6009

Now, in my quoted answer, I was not so much stating a strong opinion on this choice as I was giving a reason for the choice I was asked about, which happens to agree with our FAQ. My explanation for the contiguous range seems reasonable; why in the world would anyone choose the other?

The answer this site quotes is

Domain of Arccot

where, as I said, I was focused on justifying the domain (for the cotangent – here again, it’s really the range of arccot!) that a student had been taught, not on arguing in defense of it. Here are the two alternative versions:

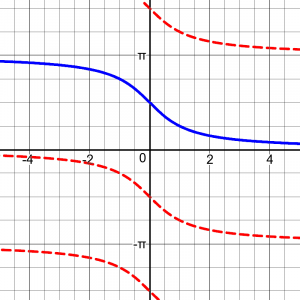
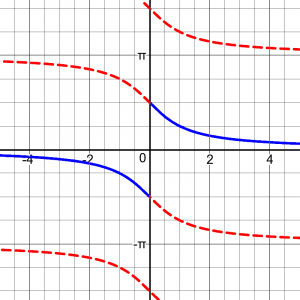
The first choice has the advantage of being continuous (making one contiguous interval), and seems to be the usual. (I made these graphs on Desmos.com, and the first is their graph of arccot(x); I had to construct the second graph piecewise.)

So, as I asked, why would anyone prefer that second one, as ugly as it is? The site that quoted me does a pretty good job of explaining it, but I might as well give my own perspective. Since one source that prefers it is Wolfram, I quoted their explanation, and analyzed that:

The following site states the convention chosen by Mathematica software:

   http://mathworld.wolfram.com/InverseCotangent.html 

   There are at least two possible conventions for
   defining the inverse cotangent. This work follows
   the convention of Abramowitz and Stegun (1972,
   p. 79) and Mathematica, taking cot^(-1)x to have
   range (-pi/2,pi/2], a discontinuity at x = 0, ...

   This definition is also consistent, as it must
   be, with Mathematica's definition of ArcTan, so
   ArcCot[z] is equal to ArcTan[1/z].

   A different but common convention (e.g.,
   Zwillinger 1995, p. 466; Bronshtein and
   Semendyayev, 1997, p. 70; Jeffrey 2000, p. 125)
   defines the range of cot^(-1)x as (0,pi), thus
   giving a function that is continuous on the
   real line R. Extreme care should be taken where
   examining identities involving inverse
   trigonometric functions, since their range of
   applicability or precise form may differ
   depending on the convention being used.

So the reason for their choice is that they want it to be always true that

   arccot(x) = arctan(1/x)

This makes sense, since

   cot(x) = 1/tan(x)

This implies that arccot and arctan have to have the same range!

I went on to look at what the corresponding identities have to look like with the usual choice of range, and it isn’t pretty. So this choice starts to make sense.

Inverse secant and cosecant

I went on to look at the inverses of secant and cosecant, whose graphs on Desmos look like this:

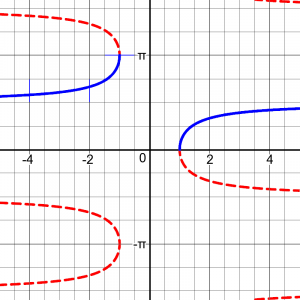
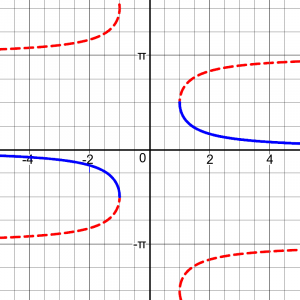
This choice of range makes good sense: the range of arcsec agrees with arccos, and the range of arccsc agrees with arcsin, and is as close to contiguous as we can get. By these definitions, \(\text{arcsec } x = \arccos\left(\frac{1}{x}\right)\), and \(\text{arccsc } x = \arcsin\left(\frac{1}{x}\right)\). But there is an interesting issue with arcsec:

I don't find as much disagreement about the range of arcsec and arccsc. Here, the usual restricted domain is [0,pi/2) U (pi/2,pi] for secant, and [-pi/2,0) U (0,pi/2] for cosecant. These follow my guidelines above, the former matching cosine and the latter matching sine. This makes their reciprocal identity work nicely, too.

The following page mentions the reason for an alternative choice, based on calculus:

  Differing Definitions of arcsec(x) Lead to Confusion over Signs
  http://mathforum.org/library/drmath/view/69193.html

On that page, I discuss the derivative of the arcsec function, which (using the usual definition) requires an absolute value: \(\frac{d}{dx}\text{arcsec}(x) = \frac{1}{|x| \sqrt{x^2-1}}\). The student had misunderstood why he wasn’t getting that result, which was a matter of keeping track of the signs of the various trig functions; no calculus is involved in that discussion. But in my final response I mentioned an article that claims that the arcsec is problematic in calculus courses, because some sources take the range of arcsec to be \(\left[0,\frac{\pi}{2}\right) \cup \left(\pi,\frac{3\pi}{2}\right)\), so that the derivative is \(\frac{d}{dx}\text{arcsec}(x) = \frac{1}{x \sqrt{x^2-1}}\). The graph is then like this:

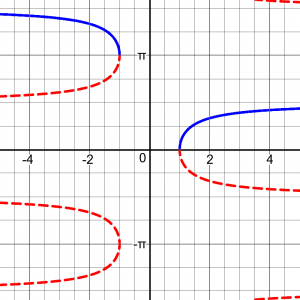
This looks very strange, with a big gap between intervals – not only non-contiguous, but non-adjacent! But it makes the derivative nicer, essentially because the tangent is always positive in this range. On the other hand, this alternative definition changes the identity: we no longer have \(\text{arcsec}(x) = \arccos\left(\frac{1}{x}\right)\), but would need something like \(\text{arcsec}(x) = 2\pi – \arccos\left(\frac{1}{x}\right)\), for x < 0.

Wolfram’s MathWorld doesn’t clearly talk about the range of arcsec (focusing instead on complex variable issues), but what they say agrees with the usual version, and the related WolframAlpha graphs the function as expected. But they present the derivative in a tricky form that avoids the absolute value: \(\frac{d}{dx}\text{arcsec}(x) = \frac{1}{x^2 \sqrt{1-\frac{1}{x^2}}} = \frac{1}{x \sqrt{x^2-1}}\) for x > 0.

I have only rarely found a graph that uses this range for arcsec, so I can’t confirm the claim that it is common. One source for the alternative range for arcsec (and a similar one for arccsc) is old editions of the CRC Standard Math Tables:

Conclusion

Ultimately, the answer to your question is (a) it's a choice, so to find what the range of an inverse trig function is, you just have to look in your text to see what they're using; and (b) the choice is made based on what will make the kind of math you're doing (trig identities, calculus, etc.) work best.

That's true of a lot of definitions in math: convenience rules!

By the way, if you are wondering about the notation I have used, like arcsin, rather than the alternative terms like \(\sin^{-1}\), see

Trigonometry Terminology