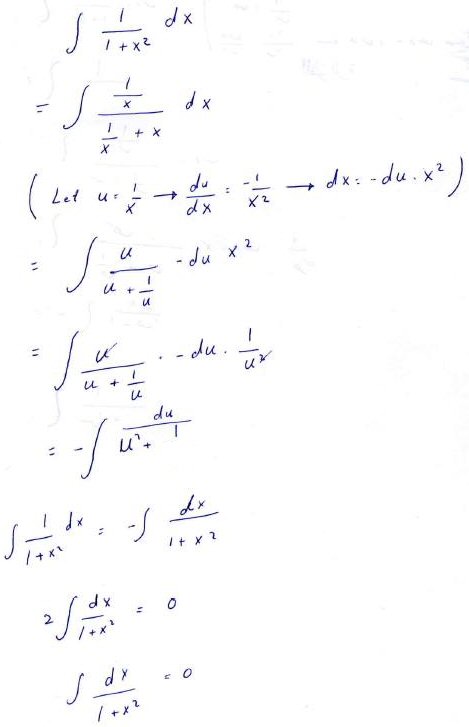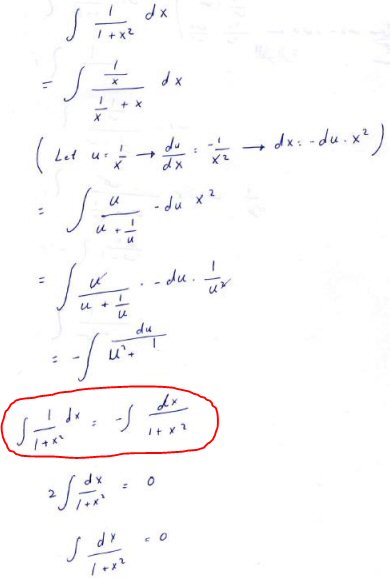Two recent questions (that came to us within two hours) dealt with apparent contradictions in integration. The first seems to give a result of zero that is clearly wrong; the second seems to give two different results for the same integral.
First question: a disappearing integral?
Here is the first question, from Amia in mid-May:
Hi Dr Math
Can you tell me what is wrong with my solution?
Thank you
Examining the details
Let’s look closely at what Amia has done. First, she rearranged and made a substitution:
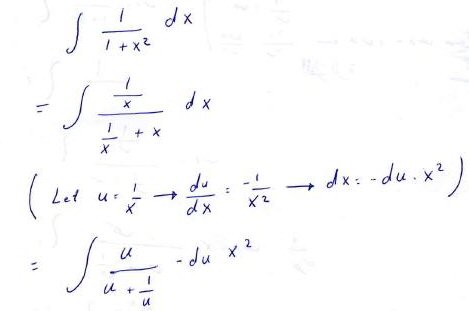
She divided the numerator and denominator by x, then defined a new variable \(u=\frac{1}{x}\) and made a substitution, which is not quite complete at this point, because both x and u are present.
I myself would have gone directly to an integral involving only u by observing that \(x=\frac{1}{u}\), so $$\frac{dx}{du} = -\frac{1}{u^2}\\dx=-\frac{1}{u^2}du$$ so we can immediately substitute and get $$\int\frac{\frac{1}{x}}{\frac{1}{x}+x}dx=\int\frac{u}{u+\frac{1}{u}}\cdot-\frac{1}{u^2}du=-\int\frac{1}{u^2+1}du$$
Amia got there with an extra step:
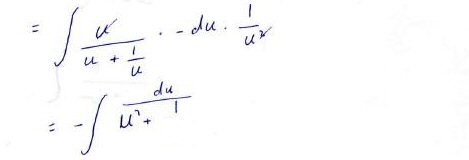
Now she has observed that this is just the negative of the original integral, except with variable u instead of x, and summarized the work so far in an equation, changing the variable and then solving for the integral:
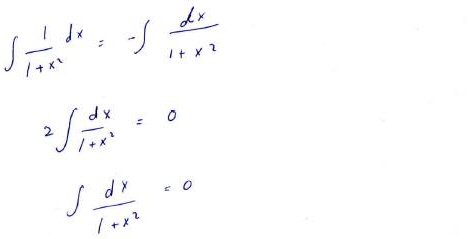
But clearly the integral can’t be zero!
(In fact, you may recognize the integral as a standard one, giving the inverse tangent. When I showed this discussion to a colleague during a lull in Zoom tutoring, she saw it that way immediately, blinding her to Amia’s work. It can be hard to see a student’s thinking when you are thinking too well yourself! I often consciously hold myself back from solving a problem to force myself to see through the student’s eyes.)
What went wrong?
Having done all this thinking and a bit more, I replied:
Hi, Amia.
Thanks for a beautiful apparent paradox! I stared at it for a while, almost convinced, before suddenly realizing what’s going on here.
Let’s look at it:
The circled line looks much like something we commonly do in integration by parts, when we get back to the original integral.
Solving for an integral (valid case)
The basic idea of what Amia does at this step, treating the integral we seek as a variable and solving for it, is not in itself invalid. Here is an example in which this is done in integration by parts: $$\int e^x\sin(x)dx$$
Integrate by parts, taking $$u = \sin(x), dv = e^x dx, du = \cos(x) dx, v = e^x$$ so that $$\int e^x\sin(x)dx = uv-\int v du =\\ e^x\sin(x) – \int e^x\cos(x)dx$$
Do it again, this time taking $$u = \cos(x), dv = e^x dx, du = -\sin(x) dx, v = e^x$$ so that $$\int e^x\cos(x)dx = uv-\int v du =\\ e^x\cos(x) + \int e^x\sin(x)dx$$
Putting these together, $$\int e^x\sin(x)dx = e^x\sin(x) – \left[e^x\cos(x) + \int e^x\sin(x)dx\right] =\\ e^x\left(\sin(x) – \cos(x)\right) – \int e^x\sin(x)dx$$
But the integral on the right is the same as that on the left; we can add it to both sides: $$2\int e^x\sin(x)dx = e^x\left(\sin(x) – \cos(x)\right)$$
Solving, we find that $$\int e^x\sin(x)dx = \frac{1}{2}e^x\left(\sin(x) – \cos(x)\right)$$
Indeed, if we differentiate this, we get $$\frac{d}{dx}\left(\frac{1}{2}e^x\left(\sin(x) – \cos(x)\right)\right) =\\ \frac{1}{2}e^x\left(\sin(x) – \cos(x)\right)+\frac{1}{2}e^x\left(\cos(x) + \sin(x)\right) = e^x\sin(x)$$
But you can’t rename the variable
Amia’s work is very similar, in that we got back to the same integral and solved for it … but notice what Amia did that was different:

But on the RHS, you have replaced an integral in u with an integral in x, just changing the name of the variable. This would be appropriate if these were definite integrals, as the variable in that case is just a “dummy variable”. But an indefinite integral is not just a number; it is a function of that variable! And in this context, you can’t just change the name of the variable.
For example, with definite integrals, it is true that $$\int_0^\pi e^x\sin(x)dx = \int_0^\pi e^u\sin(u)du$$ because the variable, x or u, appears only within the integral, rather than being a variable with a value “on the outside”. The value of each integral is a number (specifically, \(\frac{1}{2}(1+e^\pi)\)), which doesn’t depend on the variable used inside.
And in our integration by parts example, like Amia’s problem, we were working with indefinite integrals, but there we had the same variable all through the work, so everything was a function of x.
But with indefinite integrals, the variable matters. For example, \(\int 2xdx = x^2\), while \(\int 2udu = u^2\). These can be thought of as the same function of different variables (say, \(f(x)\) and \(f(u)\), but they are not the same expression, or the same value:
If we write ∫1/(1 + x^2) dx = f(x), where f(x) is a function we are trying to determine, then ∫1/(1 + u^2) du = f(u), not f(x)! They are not the same quantity, or even the same function (of x).
So that circled line in your work should really be
f(x) = – f(u) + C
We can’t solve this for f(x), so the rest of your work is wrong.
Because x and u represent different numbers, we can’t say that \(f(x) = f(u)\), so we can’t change that line to \(f(x) = -f(x)+C\), which is in effect what Amia did.
(Note that I added “\(+ C\)” without comment, because all indefinite integrals implicitly have such an arbitrary constant added on; we’ll be seeing that become important momentarily! If you include “\(+ C\)” in the integration by parts example above, you’ll find that it doesn’t affect the results; we’d just have a different constant.)
What we can determine by this method
But we do know how our x and u are related: they are reciprocals.
But we can do something interesting! Make the substitution again:
f(x) = – f(1/x) + C
This tells us a property of the function f:
f(1/x) = C – f(x)
And in fact, that property is true of the actual integral, which as you probably know is f(x) = tan-1(x). One property of this function is that
tan-1(1/x) = π/2 – tan-1(x) (for x > 0)
since the LHS is cot-1(x).
Note that here the constant C has become important. This would not work if we required C to be zero.
There are some tricky details in my mention of the inverse cotangent, as different sources use different ranges, which lead to different identities, as explained in my post Ranges of Inverse Trig Functions. My restriction to positive x avoided these issues.
I am reminded of some similar apparent paradoxes discussed here:
1=0? Calculus Says So [or Not]
The usual issue is the omission of the constant of integration (which I quietly added above); here it is much more subtle (but also much more blatant once you see it).
Keep reading, and you’ll see the same issue again. But first, let’s close the loop and find the correct answer, though I’ve already mentioned it several times.
Solving the integral correctly
When one method of integration doesn’t work, we try another. In this case, we can do a different substitution, namely letting \(x=\tan(\theta)\). Then \(dx=\sec^2(\theta)d\theta\) and \(1+x^2=1+\tan^2(\theta) = \sec^2(\theta)\), so $$\int\frac{1}{1+x^2}dx=\int\frac{1}{\sec^2(\theta)}\sec^2(\theta)d\theta=\int d\theta = \theta = \tan^{-1}(x) + C$$
Or, we might just have recognized the integrand as the derivative of \(\tan^{-1}(x)\).
Second question: two different answers for one integral?
The second question, from Tony, came in an hour and a half after the first:
Why does the integral of (1 + x)^2 not equal the integral of (1 + 2x + x^2)?
(1 + x)^3/3 is not equal to x + x^2 + x^3/3
This may not seem important, but when calculating a constant of integration the difference does matter.
Let’s check out the claim:
- The two integrands are the same: $$(1+x)^2 = 1+2x+x^2$$
- The integration is correct in each case: $$\int(1+x)^2dx = \frac{1}{3}(1+x)^3$$ by substituting \(u=(1+x)\); $$\int(1+2x+x^2)dx = x+x^2+\frac{1}{3}x^3$$
- The first integral expands to \(\frac{1}{3}+x+x^2+\frac{1}{3}x^3\), which is not equal to the second. But having done that, you might get a clue to the answer!
Doctor Fenton answered this one, pointing out how close Tony came to answering his own question:
Hi Tony,
You mention determining the constant of integration in your question, but you ignore that constant in the calculations in your question.
If you include the constant of integration and write the integral of (1 + x)2 as (1 + x)3/3 + C1 instead of (1 + x)3/3, and the integral of 1 + 2x + x2 as x + x2 + x3/3 + C2 instead of x + x2 + x3/3, and if you take C1 = 0 and C2 = 1/3, then you see that x + x2 + x3/3 + 1/3 = (1 + 3x + 3x2 + x3)/3 = (1 + x)3/3. So if you include the constants of integration with the proper values, the two answers are the same.
That is why you should always write the “+ C” when computing indefinite integrals.
To put it a little differently, if Tony had included constants in his two integrals, as $$\int(1+x)^2dx = \frac{1}{3}(1+x)^3+C_1\\ \int(1+2x+x^2)dx = x+x^2+\frac{1}{3}x^3+C_2$$ then setting them equal would yield $$\frac{1}{3}(1+x)^3+C_1 = x+x^2+\frac{1}{3}x^3+C_2\\ \frac{1}{3}+x+x^2+\frac{1}{3}x^3+C_1 = x+x^2+\frac{1}{3}x^3+C_2\\ \frac{1}{3}+C_1 = C_2$$ so that we simply have two different constants of integration.
This is very similar to the resolution of the “paradox” in the previously mentioned post, 1=0? Calculus Says So [or Not].
Both questions lead to the same lesson: In calculus (well, really anywhere in math!), you should never do anything without thinking. Renaming variables without considering the context, and blindly writing “+ C” without realizing what it means (or omitting it because you forget what it means) can leave you with confusing or simply wrong results. That’s what makes this an important thing to see!