(New Question of the Week)
Sometimes a problem leads to a very interesting discussion that brings out many good ideas – but then turns out to be something entirely different, which brings out even more (and simpler) ideas. This polynomial equation problem we helped with last week was like that. I will not be quoting the whole discussion as it took place, to avoid confusion, but just exploring some of the places we went.
The problem
The initial question was simply stated, but clearly difficult:
(x+1)(x+2)(x+3)(x+4)=99
Find the real roots of the equation above.
The direct method of solution is to expand the left side and write it as a typical polynomial: $$x^4 + 10 x^3 + 35 x^2 + 50 x – 75 = 0$$. But this is a fourth-degree polynomial equation, which is not generally solvable without great effort. I quickly checked if it had a rational root, which would have to be a factor of 75; that didn’t look promising, and in fact I could see that the answer was no, without checking all the possibilities, by imagining what the graph of the left-hand side of the original equation would look like. The equation $$f(x) = (x+1)(x+2)(x+3)(x+4)$$ would have x-intercepts at \(x = -1, -2, -3\), and \(-4\), so from my experience with polynomials I knew the graph would be something like this:
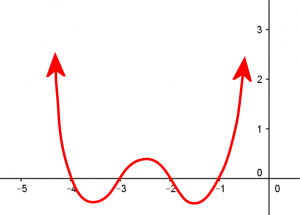
The real roots of the equation will be the points where this graph crosses the horizontal line \(y = 99\). Checking a couple values, \(f(0) = 24\), and \(f(1) = 120\), so it must cross between \(x=0\) and \(x=1\). Since we know any rational roots have to be integers, this means there aren’t any.
But from graphing, I knew that the graph is symmetrical. I don’t know a specific theorem that proves this must be true if the zeros are symmetrical as these are, but I’m sure it can be proved. (This is why I only bothered to check for a root on the right; the one on the left will be symmetrical with it.) I also had a pretty good guess that the “wiggles” in the graph would not be big enough to reach 99, so our equation would have only two real roots. (I could check that by evaluating the peak’s height, \(f(-2.5) = 0.5625\)).
A solution
At this point I was out of standard ideas; I am by no means an expert on the theory of equations, as some other Math Doctors are! But I got an idea: If we shift the graph so that its line of symmetry is the y-axis, that might simplify things. It did. So I suggested trying this:
After playing with it for a while, I discovered an idea that worked. I’m sure there are others.
I observed that the function y = (x+1)(x+2)(x+3)(x+4) is a polynomial with zeros at -1, -2, -3, and -4, and experience told me that its graph will be symmetrical about the mean of those zeros, -2.5. (Just by imagining the graph and checking some numbers, I can also see that it will equal 99 between 0 and 1, and again between -5 and -6, giving two real solutions to the equation. But the rational root theorem shows that these can’t be rational numbers.)
So I tried making the symmetry visible, by translating the graph right by 2.5, by replacing x with u-2.5. Try doing that, and see what happens.
Here is the rest of my work following this idea, which I actually wrote up later, after the solution had been found by other means:
After substitution, we have (u – 3/2)(u – 1/2)(u + 1/2)(u + 3/2) = [(u – 1/2)(u + 1/2)][(u – 3/2)(u + 3/2)] = (u2 – 1/4)(u2 – 9/4). This has to equal 99:
(u2 – 1/4)(u2 – 9/4) = 99
Letting v = u2 and expanding, we get (v – 1/4)(v – 9/4) = 99, which expands to v2 – 5/2 v + 9/16 = 99; multiplying by 16 to eliminate fractions, 16v2 – 40v – 1575 = 0.
By the quadratic formula, I get v = (40 ± 320)/32 = 45/4 or -35/2. Since this is u2 and we only want real roots, u = ±sqrt(45/4) = ±3 sqrt(5)/2.
Then, in turn, x = u – 5/2 = (-5 ± 3 sqrt(5))/2.
Incidentally, the problem was supposed to be solved without a calculator; I didn’t need one, but the work would have been a little cumbersome without it.
An easier solution
The student, in the meantime, found a different way to solve it, which is perhaps a little less intuitive and must have been accidentally discovered in an impressive bit of insight. Here is my version of what he did:
We can expand the left side partially, just multiplying (x+1)(x+4) and then (x+2)(x+3):
(x^2+5x+4)(x^2+5x+6) = 99
The interesting thing is that the factors both contain x^2 + 5x, which we can replace with t, giving
(t + 4)(t + 6) = 99
t^2 + 10t – 75 = 0
(t + 15)(t – 5) = 0
t = -15 or 5.
This implies that either
x^2 + 5x = -15 or x^2 + 5x = 5;
these yield
x = (-5 ± sqrt(-35))/2 and
x = (-5 ± sqrt(45))/2;
only the latter solutions are real, and they are the same as mine.
Like my solution, but more quickly, this reduced the quartic equation to a quadratic, which could be solved.
The real problem and a really easy solution
But in the process of discussing all this, the student revealed that he had accidentally omitted part of the problem, which should have been this:
(x+1)(x+2)(x+3)(x+4)=99
Find the sum of the real roots of the equation above.
Since the real roots were \(\frac{-5 \pm \sqrt{45}}{2}\), their sum is -5, so that is the answer.
But that problem could have been solved instantly by my original observation that the graph was symmetrical about \(x=-2.5\), and that there are only two of them:
There could conceivably be four real roots of the equation (that is, places where the graph crosses y=99), if the peak in the middle of the graph were high enough. That would happen, in fact, if we replaced 99 with 0.5. They probably chose 99 to be so high that there would be no question.
Given that fact, we don’t need to know the two real roots themselves. Because of symmetry, they will be -2.5 plus something, and -2.5 minus the same thing; their sum is -5: (-2.5 + p) + (-2.5 – p) = -5.
So most of the conversation was “wasted”, if you consider only what was actually needed in order to solve the problem; yet it took us into some very interesting areas on our long detour!
Incidentally, there is a lot known about quartic equations that is more advanced (and which I wouldn’t have used here even if I knew them well, because this problem clearly was meant to be solved simply). Here are some discussions we have had on such methods:
Ferrari's Method for Quartics Factoring Quartics Is There a 'Discriminant' for a Quartic Equation? Is There a "Discriminant" for a Quartic Equation ... in Closed Form? Solving the Quartic Solving a Quartic Equation with Substitutions
This last one shows my method, exactly – in fact, I could have copied my work and explanation from here, if I had known about it! So it wasn’t a great new discovery; but since it was new to me, it was fun.
Here is one final thought: Since both my method and the student’s depend on the symmetry of the zeros, his method should work for the problem on that last page. In fact, it does; we get the same real roots that Doctor Douglas got, and a pair of ugly complex roots as well, with considerably less work. I am curious to know whether that, too, is a well-known trick.

Pingback: Factoring a Quartic Polynomial – The Math Doctors