Some time ago we looked into the probability that a random set of sides (from, say, a broken stick) form a triangle. A recent question asked about the probability that a random triangle is acute (all angles acute) or obtuse (at least one angle obtuse), which led to more discussion of what it means for a triangle (or anything) to be random.
A proposed answer
It was not actually a question, but a request for confirmation:
A couple of decades ago I came up with the attached, which seems to show that three quarters of all possible triangles are obtuse.
My question is to ask if this treatment has any mathematical validity. If so are there any conditions on this?
Over to you!
Ian Quayle
Here is his paper:
Triangles
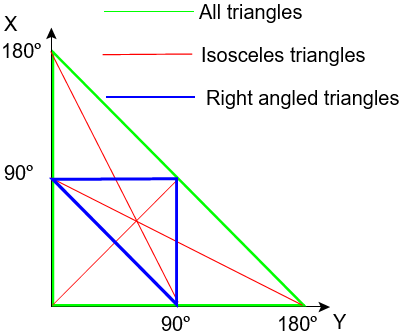
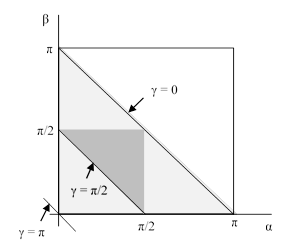
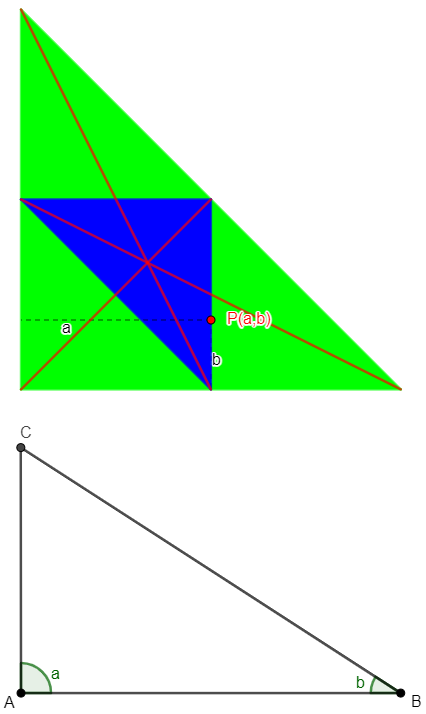
Construct any triangle from a base line and two angles.
Now, for the open-ended lines to converge and so form a triangle, x + y < 180º.
Now plot the line x + y = 180º on x, y co-ordinates as the boundary of a map of all possible values of x and y.
The green line shows the boundary of all possible values of x and y that would make a triangle.
For isosceles triangles, either:
x = y (plotted as the red line through the origin) or,
x or y = the third angle (z), in which case, for example,
x = 180º – x – y
x = 90º – y/2
and likewise, y = 90º – x/2
This gives the further two loci of isosceles triangles, also shown in red.
The intersection of the three possible isosceles triangles is the equilateral triangle.
The loci of all right-angled triangles are plotted as the three blue lines making up a right-angled triangle (isn’t that beautiful!!). This shows the three possible cases: either x, y or z is a right angle (in the latter case, x + y = 90º)
All triangles having only acute angles therefore lie within the blue boundary. The equilateral triangle, the most acute of all, lies exactly in the middle of this.
By simple geometry, the area containing only acute angled triangles is exactly a quarter of the total area representing all triangles. Hence a quarter of all possible triangles have only acute angles, the remainder have an obtuse angle.
© Ian Quayle 1999
The interior of the green triangle contains all pairs of angles \((x,y)\) that are positive and sum to less than 180°, thereby forming a valid triangle. (Points on the green triangle itself represent degenerate triangles.) Points on the blue triangle represent right triangles (with either x, or y, or their sum being 90°), and its interior represents acute triangles.
Since the area of the blue triangle is 1/4 of the green triangle (which is dissected into four congruent triangles), it seems clear that 1/4 of all triangles are acute. (And the picture is, indeed, beautiful!)
Confirmation, a caution, and an alternative
I answered:
Hi, Ian.
Yes, what you say is basically correct.
The only issue is the last line, where we need to add some conditions as you suggest.
The statement, “a quarter of all possible triangles have only acute angles” is valid only under an unstated assumption about the distribution of triangles, namely that two of the angles are chosen randomly with a uniform distribution. If they are chosen in a different way, then you would get a different result.
I notice only now that in saying “a quarter of all possible triangles”, he didn’t express what he was finding as a probability; but that is what it is. Ordinarily, we’d use his phrase to mean we’d counted all triangles, and found that 1/4 of them are acute. We can’t actually do that, which is what will lead to confusion. What do we mean by such a phrase when there are infinitely many triangles? This is where the idea of a (continuous) probability distribution will come in.
In contrast to discrete probability, we can’t count individual outcomes, but instead commonly assume that all locations are equally likely in terms of area. But this involves an assumption that is not always easy to justify: How do you know whether every point is “equally likely”, in this sense, when the probability of any individual point is zero? (It can be hard enough to decide whether all outcomes in a discrete problem are equally likely.)
We’ll get back to that. First, an alternative version of the problem:
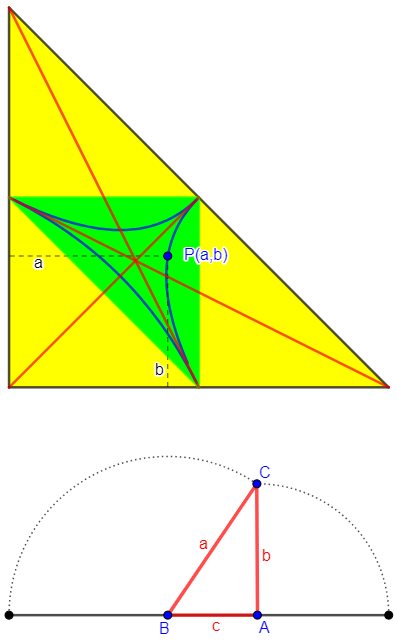
Before I got to the end, I was already thinking about at least one other way to think of a random triangle, which was to choose the side lengths randomly, rather than the angles; and, since triangles with the same angles but different sizes can be thought of as the same shape (that is, similar), we could hold the perimeter constant, say at 1. So in my version, we can choose x and y randomly, with the third side being z = 1 – x – y.
He thought of a triangle as determined by two randomly chosen angles (with a fixed side), which is different from randomly choosing two sides (with a fixed perimeter), so each will give a different answer. (We can’t just randomly choose all three sides, because they could be any real number, and a uniform distribution would be impossible.) A third option might be to randomly choose three vertices, but again we would need to restrict the region somehow.
This takes us into the realm of my post
Broken Sticks, Triangles, and Probability I
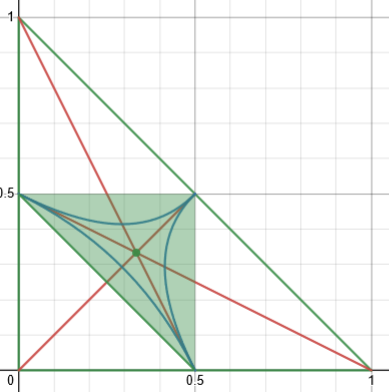
where we consider the probability that three randomly chosen lengths (with a given sum) will produce a triangle at all. (Be sure to read that, if you haven’t already, because it discusses the issue of different assumptions.) The diagrams there are reminiscent of yours. I’ve made a similar diagram (on Desmos) for my version of this problem:
Here, the red lines again correspond to isosceles triangles, and all choices of three sides adding to 1 are inside the green lines, but all actual triangles are in the green shaded region. And where are the right triangles? Between the blue curves in the middle. This gives a different answer.
Again, the green region contains all triangles (the area outside that representing sets of sides that don’t satisfy the triangle inequality); this time, the blue curve representing right triangles (and containing acute triangles) is not a triangle, so its area will be harder to calculate.
Here is a sample diagram from the referenced page about making triangles:
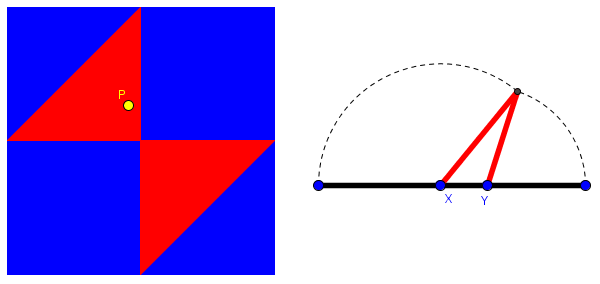
Here the red region contains all points P(x, y) where x and y are points on a unit segment such that the three segments can form sides of a triangle, as shown for point P. This shows that the probability of making a triangle is 0.25, the area of the red region.
The following link takes you to a copy of this demo that you can manipulate, moving point P to see the corresponding triangle:
Demo: Making a triangle by breaking a segment
What others have said about it
After doing this, I searched for existing discussions of this problem, and found a paper that starts with your idea, and then covers mine (and a couple wrong ones)!
Probability of a Random Triangle Being Acute
This gives your answer of 0.25 (confirming your work, but not showing your nice representation of isosceles triangles), and gives mine as 0.31776616…
For a variation of Ian’s method, they (mathpages.com) say this:
Assuming the probability density for the triangle configuration points is uniformly distributed in this space, we see that the acute triangles comprise 1/4 of all triangles.
For my method, they say,
However, there are other plausible ways of “randomly” selecting a triangle, leading to different distributions and different probabilities of being acute. …
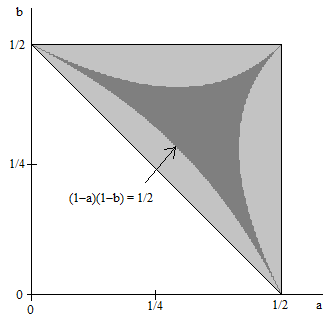
Using the normalizing condition c = 1 – a – b, we can eliminate c from these relations, and we can express the boundaries of the region of acute triangles by
These three boundary curves are shown in the figure below, outlining the region of acute triangles (the darkly shaded area) within the region of all possible triangles.
The area below the main diagonal is 1/8, so the area of the lightly-shaded region bounded by the main diagonal and the curve (1−a)(1−b) = 1/2 is given by
After a few more manipulations, they get a probability of $$12\ln(2)-8=0.31776616$$
I hadn’t worked out the actual probability from my diagram, but trusted what the author said there, because they agreed with the parts I had done!
I also found another place that combines my article’s question about sticks with my approach to this one, getting the probability that three random lengths form an acute triangle as 0.07944, which is compatible with the other:
This is a LibreText textbook (Siegrist); the section finds the probability of three parts of a stick forming an acute triangle as $$P(\text{acute})=3\ln(2)−2\approx0.07944.$$
I say this is compatible because, using our probabilities, $$P(\text{valid triangle})=0.25\\P(\text{acute | valid triangle})=0.31776616\\P(\text{acute})=P(\text{valid triangle})\cdot P(\text{acute | valid triangle})=0.25\cdot0.31776616=0.07944154,$$
giving their result.
Interactive models of both interpretations
I’ve been working on a similar diagram in GeoGebra; here it is:
Demo: Making a random triangle from sides
You can drag point P around and see the resulting triangle; here is a right triangle:
Note that in the image, P is on the blue curve, resulting in a right triangle ABC.
I also made a similar demo for your version:
Demo: Making a random triangle from angles
Again, the green region contains all actual triangles, and the blue region is acute triangles, and you can drag P around to see the triangle it represents:
So, yes, I like your work, and it leads into other interesting ideas.
Here again, P is on the edge of the blue triangle, resulting in a right triangle ABC.
Why the distribution matters
Ian replied, along with the paper I’ve inserted above.:
Hi Dave
That’s very nice to get my little idea from over twenty years ago validated by an expert. By the way, I am a well-retired professional electronics engineer who graduated nearly sixty years ago and has forgotten 90% of the maths I learnt at the time!
Regarding the distribution, I don’t understand why that is important. The area contains all possible triangles and there must be an infinity of those. There shouldn’t be a problem in saying that in that infinity of triangles, a quarter are acute. This seems to me the same as saying that a half of all integers are even.
Your GeoGebra model is brilliant and fascinating. I haven’t got round to reading Broken Sticks, Triangles and Probability, but will shortly.
Best wishes
Ian
It is not surprising that he would have trouble with what I said about the uniform probability distribution being an assumption. Most students learn only about discrete probability, which is easily explained in terms of counting, and doesn’t require thinking separately about the distribution. It is the infinite number of possibilities that makes all this tricky.
I responded:
Thanks.
Hopefully, you’ll see the point about the distribution when you read, and ponder, the linked post.
The idea is that how you choose things affects probabilities. A simple example would be that if you select numbers from 1 to 6 by rolling a die, and I do so by throwing darts at a nearby board with concentric rings labeled 1 to 6 aiming carefully at the center, and a child does the same with a distant board (trying again if she misses the board entirely), each number will have a different distribution of values. The die will produce a uniform distribution, with each number equally likely; I will produce a distribution that is almost all 1’s (assuming I’m an expert just a couple feet away); and the child may produce a distribution in which 6, on the outer ring, is more likely than anything else. The probability of each getting a particular score will be different.
All three illustrations involve randomly chosen numbers, but chosen in different ways, with different distributions. My hope was that this discrete example might help see what is happening in the continuous problem we are facing. Randomness involves some method of choosing.
In our case, you’re choosing a triangle by choosing angles with a uniform distribution, while I’m choosing sides with a uniform distribution. You’re assuming that the probability of any region on your diagram is proportional to its area, which means triangles are distributed uniformly in terms of angles; I suppose that to be true in my diagram, in terms of sides. Both are reasonable things to do; neither is an error. The “error” is just in not saying what you are assuming.
I added another discrete example:
Another example is seen in More on Gender Probability: Twins; there I mention that the probability of twins is different if you ask how likely it is for a particular child to be a twin, or how likely it is for a particular birth to be twins; there are twice as many twins as there are twin births! So how we choose what we count makes a difference in the probability. But sources often fail to state how they count.
Another similar issues lies behind Frequently Questioned Answers: The Other Child, where different ways of meeting a child result in different (and often confusing) probabilities.
More on methods of choosing
Ian still wasn’t convinced:
Many thanks for your explanation, Dave. I do understand about probability distribution, but not sure why that applies in this case. I am not choosing anything, simply covering all possible triangles. The number of possible triangles is infinite, so the probability of randomly selecting any particular triangle must be zero.
So, if we relax the problem by quantizing the possible angles into, say, seconds of arc (3600 arc seconds per degree). The number of possible triangles is (180 * 3600)^2 / 2). That’s a very big number but not infinity! You could now represent all possible triangles (quantized) then as the intersections of a fine grid aligned with the axes, within the area of all possible triangles. The intersections of the grid are 1 arc second apart and each intersection represents a unique triangle. It is clear from my original drawing that there will be only a quarter of these intersections within the “acute triangle” area.
If you quantize to even smaller angle increments, the same logic applies, so in the limit the answer remains the same. A quarter of all possible triangles are acute.
If you now wanted to apply your random selection ideas, you could draw a three-dimensional surface over my diagram, with the z axis representing probability, but is that relevant to the point I am trying to make?
Kind regards
Ian
There are two main points here: whether there is a choice being made, and how to handle infinite possibilities.
A probability distribution implies a way of choosing
I replied:
I’m taking my time trying to find a better way to explain what I’m saying, since my examples clearly didn’t work, and presumably reading my past post (and its companion) didn’t either. The beginning of the first discusses at some length how defining randomness of a particular entity requires a choice of a process for “random” selection of that entity.
You say,
I am not choosing anything, simply covering all possible triangles. The number of possible triangles is infinite, so the probability of randomly selecting any particular triangle must be zero.
I seems to me that the paper I linked to says it as clearly as I can:
Again, if the probability is uniformly distributed throughout the combined region, it follows that the probability of a randomly selected triangle being acute is exactly 1/4.
However, there are other plausible ways of “randomly” selecting a triangle, leading to different distributions and different probabilities of being acute. …
Whenever you talk about “random” anything, you have to assume some way of selecting it — even if you don’t think you are “choosing”. You need to consciously decide what distribution is appropriate (or just make it explicit), rather than unthinkingly accept some default; and a distribution is a way of “choosing”.
The mere fact that we can get different answers when we model the space of possible triangles differently should be enough to convince you that you have made a choice that affected the answer, and therefore your answer is not the only valid one.
We might compare this idea of different “models” to the existence of different map projections. In some maps, the apparent area of, say, Greenland appears larger than South America, which actually is 8 times as large. Here is the Mercator projection, compared to the equal-area Gall-Peters projection:
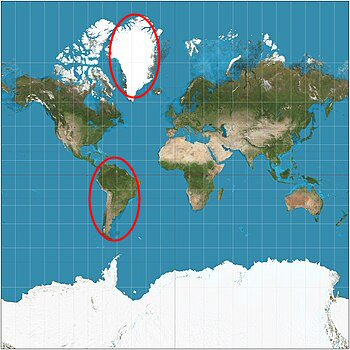
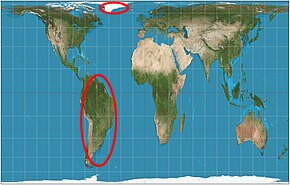
So if you asked which is a larger fraction of the earth (a larger probability of being hit if you chose a random spot on the globe), you would get a wrong answer if you used a map where area is distorted. And you’d get yet another answer if you chose a random person on the globe.
Similarly, Ian and I made different “maps” of the space of triangles, based on creating a triangle in different ways.
A continuous distribution doesn’t change things
His approach to the infinite number of possible triangles comes very close to what we do formally in calculus, and may in fact clarify the issue.
As for the fact that there are infinitely many possible triangles, that’s just what happens with any continuous distribution (as opposed to discrete distributions, where there are a finite number of possibilities, which is what students typically are most exposed to in pre-calculus courses on probability). Your thoughts there amount to a way to approach the infinite case without formally using calculus. Your area model of probability accomplishes the same thing: we assume that the probability of an event is proportional to the area representing that event.
But that assumption inherently supposes a uniform distribution of the parameters you use in your model, and other parametrizations of the probability space will correspond to different distributions that yield different probabilities. That’s what my alternative does: it uses different parameters, taken to be uniformly distributed, resulting in a different distribution of the triangles.
Taking his idea of dividing the area into tiny regions, we see that he is assuming that each of those possible regions, corresponding to a tiny range of angles, is equally likely. And they will be, if you make a random triangle by choosing a random pair of angles, using a uniform distribution for each. If you imagine making a triangle starting with something different (such as my starting with a pair of lengths), then each tiny region in my diagram will be equally likely, and my version is correct.
Both answers are correct, if we specify the problem according to our parameters. As I said at the start, the only error is in not specifying that one’s answer applies only to the specified model.


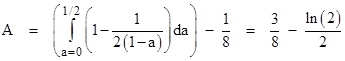
Pingback: Dealing with Infinity in Probability Problems – The Math Doctors