Average Distance Between Two Sets of Points

(A new question of the week)

Here we have a different kind of question than usual: A conjecture about distances between points, with a request for confirmation. Normally we like to just give hints to help a student figure something out; this was a request for a theorem that ought to exist, and trying to help led to providing the core of the desired proof. Since I haven’t found the theorem anywhere, let’s publish it here! In the process, we’ll see some useful ideas for problem-solving.

Can this be proved?

Here is the question, from mid-July:

Hello experts,

Thank you for having this wonderful site.

Given two sets of points (set A, set B) in 3D Euclidean space, two types of definitions of the distance between the two sets of points are considered.

The first definition is to use the average distance of all pairs of points (one point in set A, another point in set B).

The second definition is to compute a centroid of each set. Centroid is defined as the average coordinates of all points in the set. Then we use the distance between the two centroids.

I explored some examples and found the centroid distance may always be smaller or equal to the average distance. I tried to derive and prove it mathematically but I couldn’t. I assume there should be some theoretical results in math that can be used. But I’m not a math expert and not sure how to find it. My question, is it true that centroid distance is always smaller than or equal to the average distance? Is there any known theorem that can be used to prove it? Thank you so much!

Sincerely.

Jack

Here is an illustration of the idea:

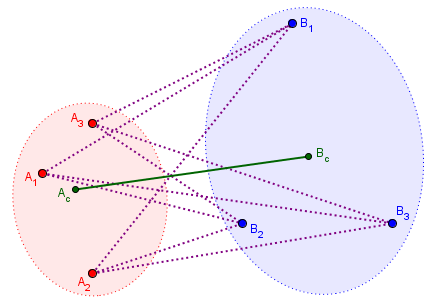
We have a set of three points in red, and another set of three points in blue. Points \(A_c\) and \(B_c\) are the centroids of these two sets. In principle, you should think of this as a three-dimensional picture; but in fact I drew it on a plane, and calculated the centroid of the set, \(A={(1,3), (2,1), (2,4)}\) as \(A_c = \left(\frac{1+2+2}{3},\frac{3+1+4}{3}\right) = \left(1\frac{2}{3},2\frac{2}{3}\right)\).

The question is: Is the distance between \(A_c\) and \(B_c\) (the green line) never greater than the average of all the distances between individual points (dotted purple lines)? It’s true in my drawing, as it was in Jack’s examples. But can we prove it?

Can we use the Triangle Inequality?

After pondering the question for more than a day, trying to search for a known theorem about this, I answered:

Hi, Jack.

I feel like there must be a familiar theorem for this, in some field, but I’m not finding it by searching related ideas (either in my mind or online). I’ve been waiting, hoping someone else will think of it!

But I can say that, in playing with it, I’m convinced that it is true, and that it can be proved based on nothing more than the triangle inequality, ||x + y|| ≤ ||x|| + ||y||. That is, the length of a sum is no more than the sum of the lengths.

Basically, since the centroid of a set of points is in effect the mean of their position vectors, your claim amounts to this:

Distance between means ≤ mean of distances

At this point, all I had in my mind was an analogy. A mean is closely related to a sum, and a distance is a length, so maybe this is just an extension of the same idea.

As indicated in the Wikipedia article I linked to, the triangle inequality can be expressed in several different ways. Geometrically, it involves the sides of a triangle:

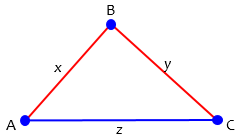
In any triangle, the sum of two sides is greater than the third side; if B were on AC, making a degenerate triangle, we would have equality. So we say in general, that for any three points, $$x + y \ge z$$ This is an instance of the fact that “the shortest distance between two points is a straight line”, since we can see \(x+y\) as a longer path from A to C than \(z\).

We are going to use this property as expressed in terms of vectors:

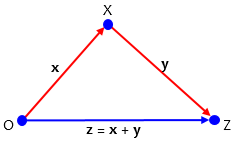
Now x and y are vectors, whose sum, z, is along the third side. So the magnitude of the sum of any two vectors is no more than the sum of their magnitudes: $$\left\|\mathbf{x}\right\|+\left\|\mathbf{y}\right\|\ge \left\|\mathbf{x}+\mathbf{y}\right\|$$

We can extend this inequality to more than two vectors, which can be proved algebraically, but is obvious, since this is again a longer path than the straight line:

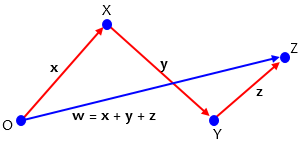
$$\left\|\mathbf{x}\right\|+\left\|\mathbf{y}\right\|+\left\|\mathbf{z}\right\|\ge \left\|\mathbf{x}+\mathbf{y}+\mathbf{z}\right\|$$

Can I prove it for a simple case?

Now I just played with the idea I had, taking the simplest possible case, with only two points in each set:

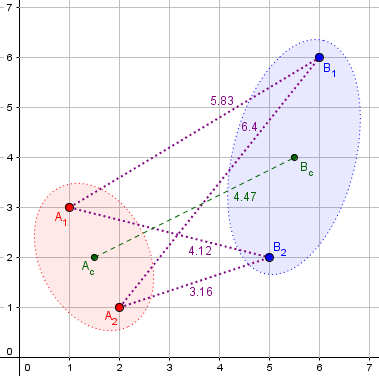
My drawing here is in a plane, but the calculations don’t assume that; that’s one advantage of using a vector formulation. The centroid of A, for example, is the average of the position vectors for the points \(A_1=(1,3)\) and \(A_2=(2,1)\), namely \(\mathbf{A}_c=\frac{\mathbf{A}_1+\mathbf{A}_2}{2}=\left(\frac{1+2}{2},\frac{3+1}{2}\right)=(1.5,2)\). The distance between the two centroids is \(\left\|\mathbf{A}_c-\mathbf{B}_c\right\| = \left\|(-4,-2)\right\| = \sqrt{20} \approx 4.47\).

For the distances measured here, we find that, as expected, \(\frac{5.83+6.4+4.12+3.16}{4}=4.8775\ge4.47\).

So I tried proving the claim for this case, with two sets of two points:

Without trying to do a general proof, let’s consider sets A = {A₁, A₂}, B = {B₁, B₂}. (Treat the points as position vectors.) Then the centroids of sets A and B will be (A₁+A₂)/2 and (B₁+B₂)/2, respectively. The distance between centroids is

||(A₁+A₂)/2 – (B₁+B₂)/2||.

There are four distances between points in A and points in B, namely

||A₁–B₁||, ||A₁–B₂||, ||A₂–B₁||, ||A₂–B₂||.

The mean of these distances is

(||A₁–B₁|| + ||A₁–B₂|| + ||A₂–B₁|| + ||A₂–B₂||)/4.

By the triangle inequality,

(||A₁–B₁|| + ||A₁–B₂|| + ||A₂–B₁|| + ||A₂–B₂||)/4 ≥

(||(A₁–B₁) + (A₁–B₂) + (A₂–B₁) + (A₂–B₂)||)/4 =

(||2A₁ + 2A₂ – 2B₁ – 2B₂||)/4 =

||(A₁+A₂)/2 – (B₁+B₂)/2||,

which is what we want to prove.

Will it generalize?

In itself, this was just one example; but it worked, which is encouraging. I didn’t want to write out a complete proof; but can we convince ourselves that it can be generalized? I thought about what would be different with more points:

So, as I thought, this is a simple extension of the triangle inequality.

If we had, say, 3 points in A and 4 in B, we’d have 12 distances, using each point in A 4 times in our sum, and each point in B 3 times; after dividing by 12, we’d end up dividing by 3 and by 4 respectively, and the same thing would happen. So what I’ve written can be turned into a general proof without too much difficulty.

And since it’s so easy to prove, it must be well-known, if I could just think what to search for …

“Easy” is a relative term! But no special knowledge seems to be required; if indeed this has never been stated before, it would have to be only because no one has asked the question! (Readers, feel free to comment if you find it stated somewhere!)

I intentionally left plenty for Jack to do, while just stepping quickly through the main points of my thinking in the expectation that he would ask about anything he didn’t understand. That’s a way of showing him respect.

Jack replied, verifying my hope that I hadn’t gone over his head:

Hello Dr. Peterson,

Wow, your proving is fantastic. Thank you so much!

I’m now wondering why I couldn’t figure this out by myself. I guess that maybe it’s too simple to have a theorem for this. Anyway, thank you again for this elegant answer.

Sincerely,

Jack

What have we learned?

I responded,

I can’t say it was obvious to me! I spent quite some time trying to find a formulation I could search for, even a theorem in statistics for the one-dimensional case involving the mean difference between two data sets.

For me, the key to solving it was just what I showed: not trying to prove it in general, but just “playing” with a very simple case to get a feel for it, and to convince myself it was plausible. In fact, the generalization that turned the example into a proof was being figured out as I wrote that; all I intended to show you was the example, with the suggestion that it could be turned into a general proof. But before I hit Send, I had to convince myself it wasn’t true only for the number 2, or when the sets have the same size!

For a final proof, I would want to write everything more generally, likely using summation notation — though that would make it a little harder to follow.

I often tell students that the way to solve a hard problem is just to start doing something. After wasting time (in some respects) trying to find a known theorem that covers this conjecture, I simply cut the problem down as far as I could (at the risk of possibly taking too special a case and making it too easy), tried it out, and accidentally made a proof! Too often students are afraid to do anything until they know what to do; they need to learn that problem-solving doesn’t require knowing the end, but only the willingness to start! (It’s also good to have enough experience to be able to recognize whether any progress has been made. But the way to get that experience is to try things!)

As I said, what I’ve given is only the outline of a proof; the actual proof would be considerably harder to understand. But the hard part is seeing that a proof exists. The rest, as they say, is left as an exercise for the reader.

To which Jack replied,

Thank you for this detailed explanation. When I worked on it, I was strangely focused on how to get rid of the magnitude operator by squaring it and I got lost in that plan to conquer it. I also played with some simple cases, but sadly I somehow forgot to use the famous “triangle inequality”. I feel like that I was trapped by myself.

To convert your example using summation notation and make it more general is nothing difficult after realizing what we want to use. I absolutely love the way you show the proof. You are great at teaching. I really appreciate your help!

If I were a mathematician, writing for mathematicians, I would not feel finished until I had written up a complete, watertight proof covering all cases. (Well, actually I’d trust them to fill in a lot of details.) But Jack’s mention of teaching is an important reminder: Our goal here is to teach, and in teaching, we need to present solutions in the way they are discovered, rather than in a final form; we need to show the way by example, rather than presenting intimidatingly perfect proofs. So I’m glad this came out the way it did.

As I was finishing up this post, Doctor Rick said the following in discussing a textbook proof with another student:

Regarding math “coming out of nowhere”, … the issue, I believe, is that many textbooks – particularly older textbooks (like 100 years ago), but some modern texts as well – tend to present math in terms of proofs and solutions in polished form, and this does not help students learn to develop proofs and solutions on their own!

In reality, the process of solving a difficult problem is frequently very messy, with false starts and floundering before one finally gets an idea that will lead somewhere promising. It requires “playing around” with a problem – trying an example before tackling a general proof, making up a similar problem with smaller numbers, etc. This sort of activity is what we at The Math Doctors, and at Ask Dr. Math before us, try to model. We will work with a student on a problem, encouraging him or her to experiment, make guesses and try them out, learn to recognize when an approach is leading nowhere and when to keep trying. It’s actually a positive thing when we don’t know the answer ourselves, so we have to flounder along with the student!

In the present case, I wasn’t really working with the “student”, but I was definitely trying to model how we think, as well as leaving room for him to polish it if he wishes. And I definitely didn’t know the answer when I started.