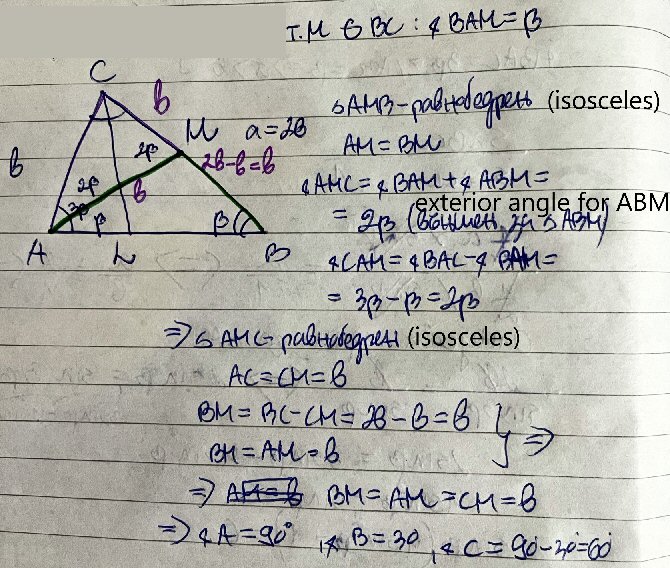(A new question of the week)
When you are given a problem about a triangle, there can be many ways to approach it: pure geometry, trigonometry, and analytic geometry come to mind. When the context doesn’t dictate a method (as turns out to be true here), you just have to try what feels right to you. This interesting problem will illustrate the difficulty we can have when we are not sure what a student has learned, but also the great flexibility we have in solving problems by multiple methods.
The problem, and initial work
Kaloyan asked this in late July, stating the problem and showing initial work, just as we like to see:
A triangle \(A B C\) is given in which \(\alpha=3 \beta\). The angle bisector of \(\angle B C A\) divides the area of the triangle in ratio \(2: 1\). Find the angles of the triangle.
Let \(C L\) be the angle bisector of \(\angle B C A(L \in A B), C L=x\) and \(\angle A C L=\angle B C L=\gamma\). Now
$$\begin{aligned}&S_{\triangle A C L}=\frac{1}{2} b \cdot x \cdot \sin \gamma \\&S_{\triangle B C L}=\frac{1}{2} a \cdot x \cdot \sin \gamma\end{aligned}$$
Since \(\angle B A C=3 \beta>\angle A B C=\beta\), then \(B C>A C\), or \(a>b\). This means that the area of triangle \(\triangle B C L\) is greater than the area of triangle \(\triangle A C L\). So
$$\frac{S_{\triangle B C L}}{S_{\triangle A C L}}=\frac{2}{1} \Longleftrightarrow \frac{\frac{1}{2} a \cdot x \cdot \sin \gamma}{\frac{1}{2} b \cdot x \cdot \sin \gamma}=\frac{2}{1} \Longleftrightarrow \frac{a}{b}=\frac{2}{1} \Longleftrightarrow a=2 b$$
I don’t know if this can be helpful later on. I was just trying to see which of the triangles \(A C L\) and \(B C L\) has a greater area and I found that relationship naturally. Something else we can notice: if we manage to express \(\angle \gamma\) with \(\angle \beta\) the problem is solved, because the sum of the three interior angles in a triangle is always \(180^{\circ}\) and we’ll have an equation in terms of \(\beta\). Thank you in advance!
Here is a picture of the problem, labeled to show Kaloyan’s initial work:
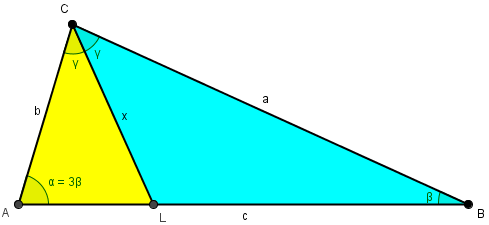
We know only the ratio of two angles, and the ratio of the two areas. We are to find all the angles.
The problem was submitted in the category of Geometry, but his work uses Trigonometry heavily, implying we are to think of it in the latter category; his work, however, could have been done entirely using geometrical theorems. For example, the ratio of the areas of the triangles, when viewed as having common base x, is equal to the ratio of their altitudes to that base, which in turn is equal to the ratio of sides a : b (and also of sides AL : LB). This is familiar as one proof of the Angle Bisector Theorem.
An interesting feature of Kaloyan’s work is that he noticed that the problem didn’t identify the order in which the two triangles have the ratio 2:1, so he took the time to determine that, rather than just draw the picture and assume. This is a mark of a true mathematician!
Keep going with trigonometry
Doctor Rick answered, suggesting a way to continue the work using trigonometry:
Hi, Kaloyan.
You have done well to determine that a = 2b. Now you can focus on triangle ABC; and you will not need to consider γ any further, either. Just use the Law of Sines and see what happens. A trig identity will probably be useful.
This seems a useful way to go, since we have ratios of angles and of sides! We’re looking only at the basics here:
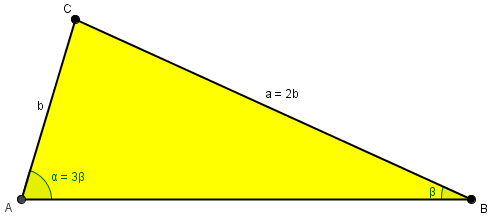
Kaloyan replied, adeptly using the Law of Sines, but then hitting a roadblock:
Hi, Dr. Rick
The law of sines gives us
$$\frac{2 b}{\sin 3 \beta}=\frac{b}{\sin \beta} \Longleftrightarrow \frac{2}{\sin 3 \beta}=\frac{1}{\sin \beta} \Longleftrightarrow 2 \sin \beta=\sin 3 \beta$$
I don’t think we have studied the trig identity that you meant because nothing comes to my mind by looking at the equality.
The triple-angle identity that we need is not always explicitly taught, but can be derived if you just know the double-angle identities.
Doctor Rick responded, assuming that Kaloyan knows at least the double-angle identity:
Good work so far:
2 sin β = sin(3β)
You may not have seen the trig identity I’m talking about — it’s not one I ever memorized, but I know that it exists. I suppose it’s clear what identity you need, isn’t it? You’d like to be able to write sin(3β) in terms of sin β (cos β may be involved too).
Do you know an identity for sin(2β)? And do you know how to derive that identity from the angle-sum identity? I suggest you start with
sin(3β) = sin(2β + β)
and use that to derive an identity for sin(3β). Then you’ll have what you need to solve the problem.
Here is the derivation of the triple-angle identity he has in mind:
We commonly memorize these double-angle identities: $$\sin(2\theta)=2\sin(\theta)\cos(\theta)$$ $$\cos(2\theta)=\cos^2(\theta)-\sin^2(\theta)=1-2\sin^2(\theta)$$ and angle-sum identities such as this: $$\sin(\alpha+\beta)=\sin(\alpha)\cos(\beta)+\cos(\alpha)\sin(\beta)$$
Using these, $$\sin(3\theta) = \sin(2\theta+\theta) =\\ \sin(2\theta)\cos(\theta)+\cos(2\theta)\sin(\theta) = 2\sin(\theta)\cos^2(\theta)+(1-2\sin^2(\theta))\sin(\theta) =\\ 2\sin(\theta)(1-\sin^2(\theta))+\sin(\theta)-2\sin^3(\theta) =\\ 2\sin(\theta)-2\sin^3(\theta)+\sin(\theta)-2\sin^3(\theta) =\\ 3\sin(\theta)-4\sin^3(\theta)$$
A solution using the triple-angle identity
Kaloyan answered, having found this identity and used it:
Hi!
I found that the angles of the triangle are 30, 60 and 90 degrees. So we’re actually dealing with a right triangle. Am I right?
Using the identity \(\sin 3 \alpha=3 \sin \alpha-4 \sin ^{3} \alpha\) we get
$$2 \sin \beta=3 \sin \beta-4 \sin ^{3} \beta \Longleftrightarrow 4 \sin ^{3} \beta-\sin \beta=0 \Longleftrightarrow \sin \beta=0 ; \pm \frac{1}{2}$$
\(\angle \beta\) must be an acute angle because \(\angle \alpha=3 \beta\) so we make the conclusion \(\sin \beta=\frac{1}{2} \Rightarrow \beta=30^{\circ}\).
To be honest we haven’t studied none of the identities you mentioned (angle-sum identity, double-angle identities). These are the identities we have worked with in school:
The solution here is very nicely stated, applying the triple-angle identity to the previously determined fact that \(2\sin(\beta)=\sin(3\beta)\), and then solving the resulting equation for the sine by factoring as \(\sin(\beta)(4 \sin ^2(\beta)-1)=0\), and then eliminating the solutions \(\sin(\beta)=0\) and \(\sin(\beta)=-\frac{1}{2}\) and the obtuse solution of \(\sin(\beta)=\frac{1}{2}\) because the angle must be acute.
So our triangle in reality looks like this:
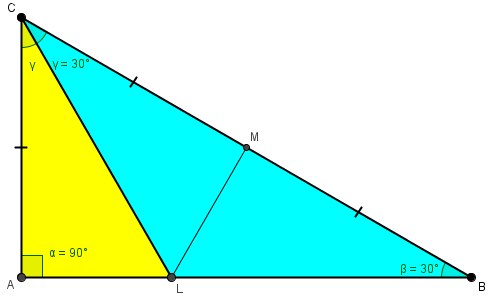
It turns out that \(\beta=\gamma\) and the three triangles shown are all congruent 30-60-90 triangles, confirming that one part has twice the area of the other. And in fact, \(90 = 3\cdot30\).
But is this what Kaloyan was expected to do, or is there another way?
Looking for an alternative
Doctor Rick responded:
I gather that you looked up the identity somewhere and used it to solve the problem. Your work is correct; the triangle does turn out to be a familiar one, the 30-60-90 right triangle. But we could not have known this without first solving the problem, as far as I can see. Of course, we could have made a wild guess that β = 30°, and checked it, discovering that we had guessed correctly.
Does the problem come from a textbook or other source directly related to the course you are taking, in which you have learned only the identities you showed? I am trying to figure out whether you are expected to solve the problem using only what you have learned, or whether the problem assumes more knowledge than you have at present – namely, the identities I mentioned.
If the problem is independent of what Kaloyan is learning, then it would make sense for it to use facts he hasn’t learned; but if it is for his class, then we need to look for an appropriate method.
Kaloyan answered those questions:
> I gather that you looked up the identity somewhere and used it to solve the problem.
You’re right.
> But we could not have known this without first solving the problem, as far as I can see.
I’m thinking in this direction at the moment. Let M be the midpoint of BC. If we manage to show that AM=MC=MB=b, then we can say α = 90° which is enough. Do you have any ideas how can we prove that? I think the best shot is to try to prove that triangle ABM is isosceles. In other words, we need ∢BAM = β. This is all I have noticed so far.
> Does the problem come from a textbook or other source directly related to the course you are taking, in which you have learned only the identities you showed?
The problem comes from my homework for the summer vacation. To be honest I don’t think my teacher has solved all the problems, so it could be her fault.
Kaloyan is now speculating about possible geometrical methods, something I often do when working on a proof, looking for a way to get to the known result. He sees several special facts about the triangle that we can see after solving it:
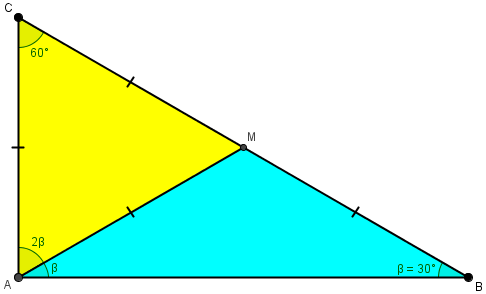
But could we determine any of these facts with only the data we were given?
Using his ideas (including the fact that \(a=2b\)), I see now that we could draw this, motivated not so much by a guess as by the ratio:
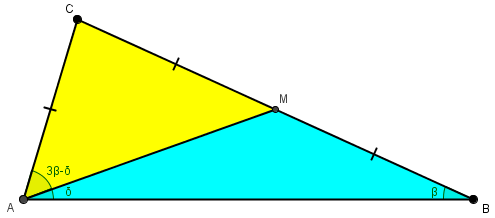
And from that, I can see a way to the goal, using his idea of showing that \(\delta=\beta\). (Can you see it?)
Starting over, without trig
Doctor Rick had a different idea, still expecting to use trig:
The problem I see with your proposal is that we would never try to prove that α= 90° if we did not have good reason to suppose that it’s true. And if we do suspect this, we can confirm it just by working out the ratios of segments based on the familiar ratios for a 30-60-90 triangle. (If AC = 1 then AB = √3 from triangle ABC, and AL = √3 / 3 from triangle ALC where angle ACL = 60°/2 = 30°. Therefore AL:LB = 1:2 as required.)
However, you give me some ideas. Let’s work with your point M from the other direction. Forgetting that M will turn out to be the midpoint of BC, we can instead construct segment AM such that M is on BC and angle BAM = β. This is one of the trisectors of angle BAC. (For completeness we can construct the other trisector of angle BAC, AN with N on BC, but I don’t think we’ll be using it.) What this does for us is to avoid needing to talk about an angle 3β.
I wonder if we can do something with this. I find myself getting confused easily because I know what I want to find, and it’s easy to forget what is established so far in this approach, as opposed to what I know from the previous work.
We are now forgetting what we know of the solution, and basing our work only on the given angle relationship:
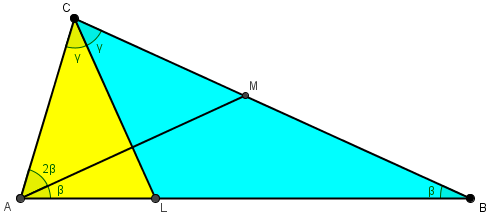
Six hours later, he had more to say:
I want to add that the problem turned out to be surprisingly easy using the approach I suggested (once I got my head on straight). In fact, far from requiring knowledge of the triple-angle identity, it can be solved with no trigonometry at all! Was the homework you mentioned for a trigonometry course, or does it make sense that it could be a basic geometry problem?
A geometrical solution
Kaloyan took that idea and ran with it:
Hi!
You’re right if I got it correctly. Here are my notes. A really nice idea (to construct one of the trisectors of angle BAC).
> Was the homework you mentioned for a trigonometry course, or does it make sense that it could be a basic geometry problem?
I really can’t answer you unambiguously. As I already told you, this problem is from my homework for the summer vacation. It is supposed to cover all of the topics we have studied in school this year (trigonometry is one of them).
He was thoughtful to add English translations of key words in his work (which I believe is in Bulgarian). Let’s write it all out here, in case you have trouble reading it:
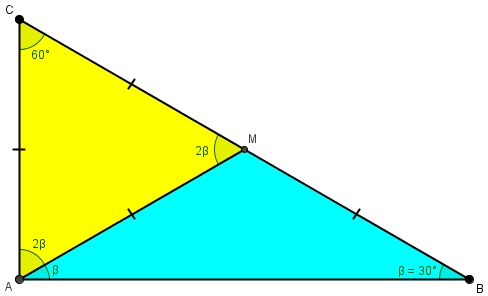
We define M as a point on BC such that \(\angle BAM = \beta = \angle ABM\). Therefore \(\triangle AMB\) is isosceles, and \(AM=BM\). Also, \(\angle AMC = \angle BAM + \angle ABM = 2\beta\) because it is an exterior angle.of \(\triangle AMB\).
On the other hand, \(\angle CAM = \angle BAC-\angle BAM = 3\beta-\beta = 2\beta\); so the base angles of \(\triangle AMC\) are equal, so that it is isosceles, with \(AC=CM=b\).
But then \(BM=BC-CM=2b-b=b\), so that also \(AM=b\). That makes \(\triangle AMC\) equilateral, so that \(2\beta=60^\circ\), \(\beta=30^\circ\), and \(3\beta=90^\circ\), giving us a 30-60-90 triangle. Once again, we have the actual triangle looking like
A variation
Doctor Rick approved, and gave his own version of the solution, reminding Kaloyan that even the first part of his work (done originally with trigonometry) did not need trigonometry, so that this is an entirely geometrical solution:
I think we’ve got it!
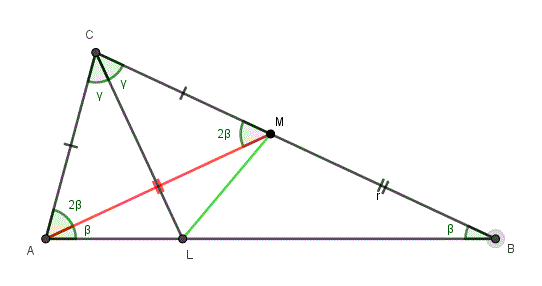
Do you see how your conclusion that BC = 2(AC) can be reached without trig? My figure is attached.
I worked out that AC = MC and AM = MB first, without yet using the given information that the angle bisector of angle ACB divides the area of triangle ABC in the ratio 2:1.
Then, adding one more segment, LM, I observe:
(1) triangle LAC is congruent to triangle LMC by SAS.
(2) If the area of triangle BLC is twice the area of triangle ALC, then triangles CML and BML must have the same area.
(3) These triangles have a common altitude from L, so their bases (MC and MB) must be equal.
Now we know (as you saw) that AC = MC = AM, so triangle AMC is equilateral and 2β = 60°. The rest follows. No trig, just basic geometry!
The last part of the work proved that \(a=2b\), without having previously used that fact.
We got several complete proofs for the price of one!