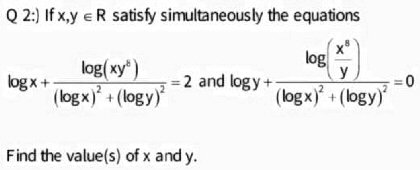(A new question of the week)
We’ll look at a very complicated logarithmic equation, which leads to quartic equations and some very interesting graphs. We won’t find a fully satisfying solution method, but we’ll have some fun trying – and reveal the fallibility of at least one Math Doctor!
Simplifying an “ugly” problem
The problem came from Zawad at the end of July:
I can’t find how to start.
That’s about as ugly a log equation as I’ve ever seen!
Incidentally, there is nothing here to indicate what base is intended for the logs; at the high school level, “log” commonly means the “common log”, using base ten, but at higher levels it can mean the natural log, with base e. We’ll find out in Zawad’s responses that base ten is at least what he expects it to mean!
I didn’t have a complete solution, but I could at least offer a way to start:
Hi, Zawad.
I would start by changing variables, defining u = log(x) and v = log(y). Then write the equations in terms of u and v.
It will still take work, but it will look a lot more familiar!
This is a standard way to make the “ugly” a little less so, when certain expressions appear repeatedly. Here, x and y appear only within logarithms, and we know we can expand each logarithmic expression in terms of the two basic logs.
Zawad tried out my suggestion:
Let log x = u, and log y = v.
u + {(u+v⁸)/(u²+v²)} = 2
v + {(u⁸-v)/(u²+v²)} = 0
So, u = 1, v = -1.
Now, log x = 1, so x = 10.
And log y = -1, so y = 1/10.
The basic ideas are right, but he’s made a simple error at the start, one that is very easy to make when you do too much at once. The first steps need to be written out in detail to be sure they are right.
Three levels of errors
I had several comments to make on the work:
At first, I thought you had done well with my little hint. But there are two problems with this solution. Make that three.
First, unfortunately, log(xy8) = log(x) + 8log(y) = u + 8v, not log(xy8) = log(x) + log(y)8 = u + v8. So your new equations are wrong.
This was just a little slip, but totally changed the problem! The good thing was, this allowed me to talk about subsequent errors without giving away the answer.
Second, you don’t show how you found the solution, but I suspect you found it by inspection, simply seeing that (1, -1) works. This doesn’t prove that that is the only solution.
The solution of the (incorrect) system $$\left\{\begin{matrix}u + \frac{u+v^8}{u^2+v^2} = 2\\ v + \frac{u^8-v}{u^2+v^2} = 0\end{matrix}\right. $$ is not obvious! But if we just guessed small whole numbers, we could find that in fact, if \(u = 1, v = -1\), then $$\left\{\begin{matrix}u + \frac{u+v^8}{u^2+v^2} = 1 + \frac{1+(-1)^8}{1^2+(-1)^2} = 1 + \frac{2}{2} = 2\\ u + \frac{u^8-v}{u^2+v^2} = (-1) + \frac{1^8-(-1)}{1^2+(-1)^2} = -1 + \frac{2}{2} = 0\end{matrix}\right. $$
But we want all solutions, and finding one doesn’t mean we’ve found them all:
In fact, if I graph your (wrong) system of equations (using Desmos), I find that there are four solutions:
Of course, that’s not the right graph!
I wouldn’t have shown this graph if it had been for the right equation; but it was a nice way to show (spectacularly) that while \((1,-1)\) is a solution, there are others, one even being the “trivial” solution \((0,0)\). Well, not really … try it out in the equations and see what you get!
(Incidentally, while Desmos is amazing in graphing this sort of equation, in this case it doesn’t show intersections when I select one of the equations, as it does in simpler cases. I had to plot the four apparent solutions myself. I’m not sure whether this is intentional; but the result is that I can’t blame Desmos for my claiming an extraneous root as real. I simply failed to check … after pointing out the importance of doing so!)
Third, you didn’t check your solution in the original equations. If we put (10, 0.1) into the second equation, for example, we get 3.5, not 0.
This is a common error in solving an equation by substitution. Even when we remember to check our solution of the new equation, and back-substitute to get the solution of the original, it will be wrong if we had made a mistake in the substitution itself – as we did here. But the very ugliness of the original equation leads us to want to avoid that check. But let’s do it, plugging in \(x=10,y=0.1\):
$$\left\{\begin{matrix}\log(x)+\frac{\log\left(xy^8\right)}{(\log(x))^2+(\log(y))^2}=2\\ \log(y)+\frac{\log\left(\frac{x^8}{y}\right)}{(\log(x))^2+(\log(y))^2}=0\end{matrix}\right. $$
$$\left\{\begin{matrix}\log(10)+\frac{\log\left(10\cdot 0.1^8\right)}{(\log(10))^2+(\log(0.1))^2} =1+\frac{\log\left(10^{-7}\right)}{1^2+(-1)^2}=1+\frac{-7}{2}=-2.5\ne 2\\ \log(0.1)+\frac{\log\left(10^9\cdot 0.1\right)}{(\log(10))^2+(\log(0.1))^2}=-1+\frac{\log\left(10^9\right)}{1^2+(-1)^2}=-1+\frac{9}{2}=3.5\ne 0\end{matrix}\right. $$
Try again. The correct system in (u, v) is not much easier; it’s possible to find each solution by guess-and-check (unlike your system), but you still wouldn’t be sure you didn’t miss anything.
I will admit that I have not yet pursued the problem far enough to see a nice algebraic way to find all solutions. I cheated by making the graphs (only to check your work).
May I ask where this problem came from? Does the source imply that it should be quickly solvable, or that it should be very challenging (or both)? It’s definitely interesting!
My main goal here, besides getting Zawad on the right track, is to avoid implying that the rest will be easy!
Correcting the errors
Zawad wrote back:
At first, I’m sorry for my mistake.
Let log x = u. and log y = v
So,
u + {(u+8v)/(u²+v²)} = 2……(1)
v + {(8u-v)/(u²+v²)} = 0……..(2)
(u, v) = (-1, 2). or, (u, v) = (3, -2).
[I haven’t understood how to solve the two equations. So, I used Wolfram Alpha]
So,
log x = -1. x = ⅒
log y = 2. y = 100.
Again,
log x = 3. x = 1000.
log y = -2. [It’s not possible]
(x, y) = (⅒, 100).
Now, I’m humbly requesting you to tell me the process of solving the two equations (1 and 2). One of my friends has found the problem. But none has solved it yet which is very sad for us. Thanks.
I suspect the mistaken rejection of the second solution may be due to confusing the impossibility of taking the log of a negative number, with the log itself being negative.
Zawad has “cheated” even more than I had, using not just a grapher but a solver. Here is what Wolfram Alpha reveals:
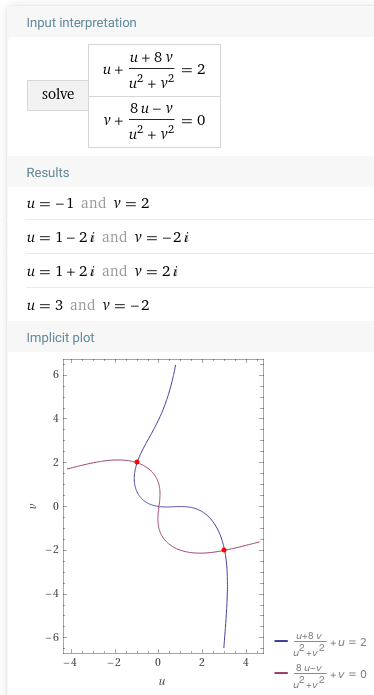
So there are four solutions, two real (which perhaps are all we are required to find?); and there’s an interesting feature you may notice in the graph.
A partly correct correction
I had some corrections and comments (which, unfortunately, I made without checking what Wolfram Alpha did, but just using the graph I’d made):
There are three solutions; your second solution does work (why do you say not possible?), and there is another (trivial) solution.
But so far, I have only found them either by “guess and check” (setting one variable to integers and seeing if both equations have a common solution for the other variable), or by graphing the equation in u and v on Desmos. I am with you in not yet having a proper algebraic solution.
Again, where did the problem come from? Not all equations can be solved algebraically, so I would want some evidence that it is intended to be solved that way. Presumably this is some sort of contest problem, and there may be some special trick I haven’t seen yet. Perhaps another of us has an idea. But don’t be “very sad”!
I was wrong about the third solution, because I depended too much on my Desmos graph! We’ll see that momentarily. Wolfram Alpha, too, can make mistakes, but here it clearly shows only two (real) solutions, and it turns out to be right.
Zawad only had questions at this point:
Yes, the second solution is possible. But what is the third trivial solution? How to solve that?
May be it’s a problem of a contest.
I now compounded my error:
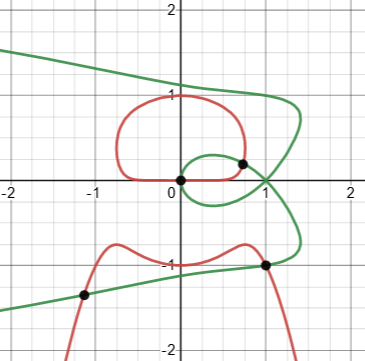
Here is the graph I made, showing all three solutions to the equation in u and v:
You can see what I mean by “trivial”. It isn’t obvious when you just look at the equations, but it is the first thing one should try.
The trouble is, Desmos, as we already saw in the wrong graph, fails to show or even recognize “holes” in graphs. That trivial solution at \((0,0)\) is extraneous, because it requires division by zero.
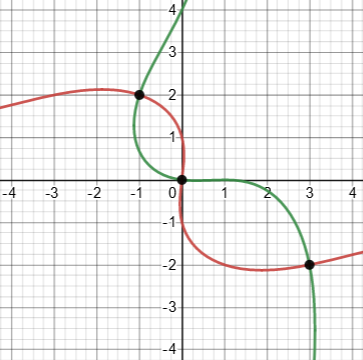
Here is the graph of the original equations, on which only the trivial solution is visible:
The other two, of course, require zooming in on the appropriate places. One might not even think to look at all.
I am continuing to think about the problem as I have time.
Again, the trivial solution is not really a solution at all, so this graph lies in two ways: It shows a “solution” that is not, and it hides the solutions that are! Notice that the curves look as if they were becoming parallel as they extend in both directions, but they are not. Here are stretched versions of the graph to show the real solutions:
\((0.1,100)\)
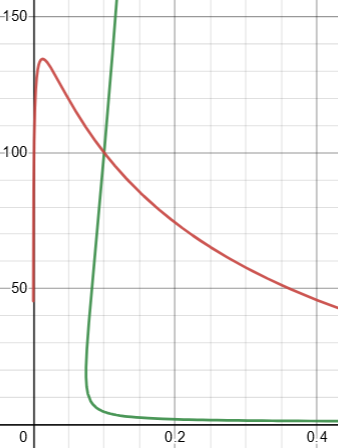
\((1000,0.01)\)
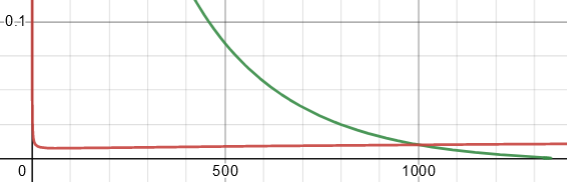
You’d never guess these behaviors!
An algebraic solution
A day later, with no further responses, I reported my status:
I’ve found an approach that at least comes close to giving an algebraic solution.
Seeing that u2 + v2 appears in both equations, it occurred to me to express u and v in polar coordinates, letting u = r cos(θ) and v = r sin(θ). This led to a somewhat simpler system of equations, which I could turn into a fourth degree equation that can be factored (though that’s not easy). It leads to the two non-trivial solutions; the trivial solution had been lost by having assumed r ≠ 0, so it would have to be checked separately.
There is probably a better way; I am omitting details in the hope that you will follow a different path from my hint and perhaps improve on my work.
This was the end of the conversation; but here is what I did:
Our correct system of equations was $$\left\{\begin{matrix}u + \frac{u+8v}{u^2+v^2} = 2\\ v + \frac{8u-v}{u^2+v^2} = 0\end{matrix}\right. $$
The substitution $$u = r\cos(\theta), v = r\sin(\theta)$$ yields $$\left\{\begin{matrix}r\cos(\theta) + \frac{r\cos(\theta)+8r\sin(\theta)}{r^2\cos^2(\theta)+r^2\sin^2(\theta)} = 2\\ r\sin(\theta) + \frac{8r\cos(\theta)-r\sin(\theta)}{r^2\cos^2(\theta)+r^2\sin^2(\theta)} = 0\end{matrix}\right. $$ which simplifies, after applying an identity to the denominators and multiplying both sides of each by \(r\), to $$\left\{\begin{matrix}r^2\cos(\theta) + \cos(\theta)+8\sin(\theta) = 2r\\ r^2\sin(\theta) + 8\cos(\theta)-\sin(\theta) = 0\end{matrix}\right. $$
(Observe that multiplying by \(r\) assumes it is non-zero, eliminating the (non-existent) “trivial” solution!)
Dividing everything by \(\cos(\theta)\), we get $$\left\{\begin{matrix}r^2 + 1+8\tan(\theta) = 2r\sec(\theta)\\ r^2\tan(\theta) + 8-\tan(\theta) = 0\end{matrix}\right. $$
Solving the second equation for \(\tan(\theta)\), we get $$\tan(\theta) = \frac{8}{1-r^2}$$
Replacing this in the first equation, and using the fact that \(\sec^2(\theta) = 1 + \tan^2(\theta)\), we get $$r^2 + 1+\frac{64}{1-r^2} = \pm 2r\sqrt{\left(1+\frac{64}{(1-r^2)^2}\right)}$$
Multiplying both sides by \(1-r^2\), we get $$(r^2+1)(1-r^2) + 64 = \pm 2r\sqrt{\left((1-r^2)^2+64\right)}$$
Expanding, squaring, and expanding again, we get the polynomial equation $$r^8-4r^6-122r^4-260r^2+4225=0$$
That’s really a quartic equation in \(r^2\), and (with effort) it factors as $$(r^2-5)(r^2-13)(r^4+14r^2+65)=0$$
This leads to four (apparent) real solutions, $$r=\pm\sqrt{5},\theta=\cot^{-1}\left(-\frac{1}{2}\right)\\ r=\pm\sqrt{13},\theta=\cot^{-1}\left(-\frac{3}{2}\right)$$ and four imaginary solutions, which I will ignore because they will involve taking the inverse tangent of a complex number, which takes us into even stranger territory.
These solutions yield $$u = r\cos(\theta) = \pm\sqrt{5}\cdot\frac{-1}{\sqrt{5}}=\pm 1\\ v = r\sin(\theta) = \pm\sqrt{5}\cdot\frac{2}{\sqrt{5}}=\pm 2$$ and $$u = r\cos(\theta) = \pm\sqrt{13}\cdot\frac{-3}{\sqrt{13}}=\pm 3\\ v = r\sin(\theta) = \pm\sqrt{13}\cdot\frac{2}{\sqrt{13}}=\pm 2$$
Pairing these off appropriately, we get our solutions in u and v, \((-1,2), (3,-2)\). And from that, the solutions to the original problem in x and y are \((0.1,100), (1000,0.01)\).
This wasn’t pretty. Feel free to comment if you see nicer ways to solve the problem!