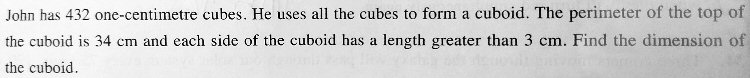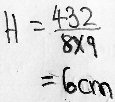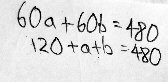(A new question of the week)
A couple recent questions involved factoring numbers, in interesting ways. One involves the volume and perimeter of a block of cubes, and the other involves finding numbers with a given HCF (Highest Common Factor) and sum. Both illustrate thinking through a non-routine problem about factors.
Problem 1: A cuboid
Both came from Matt, who submitted them about 5 minutes apart in early July. Here is the first:
Hello.
I need some help (hints).
Thanks
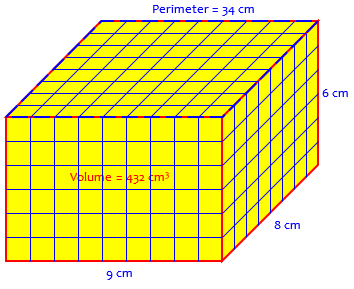
A cuboid is what I grew up calling a “rectangular parallelepiped”, which certainly deserves a simpler name! Here is a picture of the problem:
Leading the giraffe to leaves
In submitting this question, Matt called himself “Matt the Math Giraffe”. Doctor Rick answered with a good guess about the meaning of the name:
Hi, Matt. What’s this about a giraffe? Are you just tall for your age, or are you stretching higher to reach the more challenging math problems?
I don’t know what math you have learned, so I can’t be sure what hints would be appropriate, but I think that no matter what, there will be some “guess and check” involved. However, by applying some thought, we can reduce the number of possibilities to be checked. I call this “intelligent search“.
First … What ideas come to your mind as you read the problem? You know what a cuboid is, right? What does the fact that the perimeter of the top is 34 cm tell you about the length and width?
Since we know all the dimensions of the cuboid will be whole numbers of centimeters, it will be useful to factor the number 432. Do you have an idea why I say that?
Right now, I’m just pointing out some nice leafy branches up there; I’ll let you do the reaching. Tell me your thoughts and discoveries, and I can help you make use of them.
Matt has told us, directly and by analogy, that he just wants some hints to direct his thinking. Will these be enough?
He wrote back:
Yes, you’re right. I do challenging maths everyday so I’m a giraffe (lol).
So I discovered that to find the sum of length and width of the top of the cuboid (I only saw this when I drew a cuboid) = 34 cm ÷ 2 = 17 cm
Hmm so what do I do next? I bet I need to find the prime factorisation of 432 cuz this topic is about prime factors and I also want to find the factors = 432 = 2^4 × 3^3.
This is an excellent start: If the length and width are L and W, then the perimeter of the top is \(L+W+L+W = 2(L+W)\); so their sum is half the perimeter, or 17 cm.
And he’s correctly found the prime factors, \(432 = 2^4\cdot 3^3\). So we don’t need to go through how to find them.
But the reason for factoring is not just that that is what has just been taught; it’s because the problem calls for it. We’ll discuss why.
But what to do next?
Rephrasing the problem
Doctor Rick replied, suggesting a useful next step:
You have done good things to start with. Do you have no ideas of your own yet?
Since I know you’re up for a challenge, I don’t want to give you too big a hint.
Let’s just work on rephrasing the goal of the problem in terms of numbers alone (no cubes or cuboids or centimeters). The problem said:
John has 432 one-centimeter cubes. He uses all the cubes to find a cuboid.
The perimeter of the top of the cuboid is 34 cm, and each side of the cuboid has a length greater than 3 cm.
Find the dimensions of the cuboid.
What we want is to find the dimensions — three numbers: the length, width, and height (in centimeters). Can we call them L, W, and H? Or do you prefer x, y, and z?
I already pointed out what you also probably saw right away: that the three numbers must be positive integers (whole numbers).
You have found that the second line above tells us the sum of the length and width is 17.
What else can you say? I want to write the problem as, “Find the values of the positive integers L, W, and H given that … “
Reformulating a problem is a key step; we need to turn it into a mathematical form, so we can use the tools we have.
Making a guess
Matt responded:
It has something to do with the factors of 432? Since the length is supposed to be longer than the breadth so length must have a bigger number.
I can’t seem to find the dimensions. I took 17/2 = 8.5 then I think its 8 × 9 because 8 + 9 = 17 cm (I found that earlier) but I don’t think it’s right, I have not gotten the concept.
Students told to divide a number into two parts often first think of dividing by 2; and that can in fact be a quick start for finding a pair of numbers close to one another whose sum is given. But there are several other pairs that add to 17; we don’t know that they have to be this pair.
Doctor Rick became a little more explicit in his hint about 432:
I have been waiting for you to say something that may be so obvious that you just didn’t bother mentioning it. I’m thinking of the fact that the product of the length, width, and height must be 432. Is this obvious, or did you not see it yet?
To answer my own question from last time, we could state the problem this way:
Find the values of positive integers L, W, and H given that L, W, and H are greater than 3, LWH = 432, and L + W = 17.
Now, you have a good guess that L and W are 8 and 9. (It really doesn’t matter which is which.) Can you find what H would be in that case, and check whether these values satisfy the conditions?
If they do, I would still want to see whether this solution is unique — that is, I’d prefer to be sure I have found all solutions. We can talk about that.
“Length” doesn’t always mean the longer dimension; but it doesn’t hurt to make it so, for the sake of specificity.
And although 8 and 9 is not the only possible pair, it doesn’t hurt to make a guess and check it; as we’ve often seen here, that can be a way to improve your understanding of a problem. But the “guess-and-check” method can never convincingly find all solutions to a problem, or show that you have the only one.
Checking the guess
Matt replied, finishing the work for his guess:
Oh, I just noticed that 432 must be the product of L, W and H. For the L and W, how do you find them in the right way? I just made a guess that I took 17/2 but I don’t know the real meaning of this. Here’s my solution for H.
So, if the length and width are 8 cm and 9 cm, then the height is 6 cm; and this appears to be a valid solution. But there’s more to do!
Doctor Rick answered:
Good! Let’s check your solution (L, W, H = 9, 8, 6) against my restatement of the problem:
Find the values of positive integers L, W, and H given that L, W, and H are greater than 3, LWH = 432, and L+W = 17.
Are all three numbers positive integers? Yes. Are they greater than 3? Yes. Is LWH = 432? Yes. Is L + W = 17? Yes. So we have one confirmed solution.
But you just guessed, and then we checked the guess. That’s not a wrong way to solve the problem, but it doesn’t tell us whether there might be other solutions. So now let me show you my “intelligent search” method.
An intelligent search
Intelligent search means making a series of “guesses” guided by understanding of the problem, so that we can be sure to cover all possibilities, but without wasting effort.
We start with your observation that L + W = 17. Instead of just picking one pair of positive integers that add to 17, let’s list all of them:
1 + 16
2 + 15
3 + 14
4 + 13
5 + 12
6 + 11
7 + 10
8 + 9
That’s it. Now, we consider the condition that LWH = 432 = 24 · 33. Since L, W, and H are all integers, each must divide 432. We can start by eliminating every pair above in which one of the numbers has a prime factor other than 2 and 3. What’s left? Only 1 + 16 and 8 + 9. But the first of these is eliminated because one number is 3 or less. (I only included the first three pairs in my list because I was curious what effect the greater-than-3 requirement would have; otherwise I would have had only five pairs to check.)
We could also think of this as eliminating numbers that are not factors of 432; knowing the prime factors helped us quickly recognize them.
The problem could have just required more than one layer in the cuboid, rather than saying all dimensions are greater than 3.
We still need to check that 8×9 is a factor of 432; this is not guaranteed. For instance, if 4 + 16 had been in the list, each number individually divides 432 but their product does not. But we have already confirmed that 8 and 9 work as a solution, so we are done.
Thus, by a search for all possibilities (an “exhaustive search”), we have found that the solution you found is the only one: The dimensions of the cuboid are 8 by 9 by 6. What do you think?
Here is the solution:
Looking back on the problem
Matt responded:
Thanks, so now I know the product of the L, W, H must be divisible by 432 to find the dimension. I understand now.
Doctor Rick saw a problem there:
I don’t think you meant exactly what you said … and in math, precise language is important.
The product of the length, width, and height (LWH) isn’t divisible by 432, it is 432 — because 432 1-centimeter cubes were used in making it, so its volume is 432 cubic centimeters; and the volume of a cuboid (in cubic centimeters) is the product of its length, width, and height (in centimeters).
Divisibility comes into the method of solution because all three dimensions are whole numbers of centimeters. Therefore 432 must be divisible by H, and by L, and by W — because, for instance, 432 = L times (WH), so 432 divided by L is the whole number WH, with no remainder, and that’s how divisibility is defined.
Quite likely Matt knew all this; but learning to say accurately what you mean is an essential part of learning math. Sometimes if you say it wrong, you will then think wrongly!
(I don’t have a clear idea of what math you have learned so far. Looking over some of the questions you have asked us about, it looks like you’re doing some first steps in algebra — I don’t see a lot of working with equations. So I just want to be sure that you understand the notation I have used: LWH (putting three variables next to each other) means that their values are multiplied. I’m pretty sure you know that the volume of a cuboid is its length times its width times its height, and that’s what LWH means. This may not have been a problem for you, but since you didn’t catch on right away about the product being 432, I thought I should make sure I didn’t miscommunicate.)
This is a common problem in answering questions: Not knowing a student’s background, we may say either more than they need, or less. We try to use whatever clues we are given to understand the student, as well as the problem!
Now, what were the key ideas in this problem?
One way to look at the problem is that we want to split up the factors of 432 into three groups (L, W, and H) that meet the conditions of the problem, particularly that the sum of two of these is 17. We have
432 = 2 × 2 × 2 × 2 × 3 × 3 × 3 = (2 × 2 × 2) × (3 × 3) × (2 × 3) = 8 × 9 × 6Since the first two of these add up to 17, and all three are greater than 3, this way to split the factors meets all the conditions.
Matt concluded:
Yeah I actually meant that 432 should be divisible by L, W, H instead. The factorisation method you mentioned is also a great way to check the working!
Problem 2: HCF and sum
That discussion took place over 6 days. Meanwhile, there was another discussion of Matt’s second problem submitted at the same time:
Hello.
I need some help with part b. I doubt is trial and error, right?
Thanks math doc.
Both parts are interesting, in that they ask for multiple solutions, giving more emphasis to the hidden possibility in the first problem that the solution might not have been unique. We won’t be discussing part (a); if you do it, you’ll find that there are exactly two solutions, not more than two as the wording allows for. In part (b), we have no clue how many we need to find.
In case you are not familiar with the terms, HCF means Highest Common Factor; other terms used for it are GCF (Greatest Common Factor) and GCD (Greatest Common Divisor). So 60 is a factor (divisor) of both numbers, and they have no higher common factor than 60. You can read more about it here.
I think Matt recognizes that trial and error alone can’t guarantee finding all possibilities, so something more will be needed … perhaps an intelligent search? (At this point, Doctor Rick hasn’t yet written.)
Doctor Fenton answered this one, again trying to give only a little hint:
There’s a very small amount of trial-and-error, but not much. You know that 60 is the HCF of the two numbers, call them n and m. In particular, 60 is a factor of n and of m. What does that tell you? What else does the problem tell you about n and m?
Matt replied, essentially just making a guess:
n and m has common factors of 2^2 x 3 x 5.
So if I take n = 60, then m will be m = 420.
But there’s only 1 pair of numbers??? The question asks for pairS so how do I find all the other numbers?
He has made the smallest possible guess for the first number, used the sum to find the other, and (hopefully) checked that the HCF of 60 and 420 is 60. (It is.)
From factors to multiples
Doctor Fenton took his hint just one step further:
Since 60 is the HCF of n and m, then 60 is a factor of n and of m. Another way of saying that is that n is a multiple of 60, and so is m. What does that tell you about n and m?
Matt didn’t quite get the hint yet:
Both must have multiples of 2, 3, 5.
But I don’t know how to make the two numbers have these multiples/factors.
I think he means the numbers will both be multiples of 2, 3, and 5, the prime factors of 60. Students often struggle with the terminology here, which again can lead to wrong thinking as well.
I jumped in with a further hint, pointing out what to us seems obvious from the word “multiple”, but clearly is not yet so to Matt:
Possibly what Doctor Fenton is suggesting (at least this is what I would do) is that if m and n are both multiples of 60, then we can write them as m = 60a and n = 60b, where a and b are integers. (Something else has to be true of a and b, which I’ll let you discover.)
If the sum of m and n is 480, what can you say next?
To say “this is a multiple of that” means “this is that multiplied by an integer“. And writing it explicitly that way is what allows us to start writing equations.
Matt was flailing:
Is a + b = 360??? I don’t know how to solve.
The sum tells us that \(m+n=480\); this seems to be just a wild leap. We need to get Matt back on firm ground.
Doctor Fenton affirmed my suggestion, and added the next step, the way to use the two expressions:
How did you get that a + b = 360?
The problem gives you pieces of the answer, but you have to put the pieces together. As Dr. Peterson suggested, I was trying to get you to write that since 60 is a factor of m and n (since it is the HCF, so in particular it is a factor of m and n), that means that there are integers a and b such that m = 60a and n = 60b.
The problem tells you that the sum of m and n is 480. Can you write an equation for that? Can you make that equation into an equation involve a and b?
Matt wrote the right equation, but made an algebra mistake:
I thought of it for quite a while, but still can’t get it
Finishing up
Doctor Fenton answered:
The equation
60a + 60b = 480
is NOT the same as
120 + a + b = 480.
The term 60a is the product of 60 and a, 60 multiplied by a, which is NOT the same as 60 + a.
You can’t just add the coefficients of 60a + 60b and get (60 + 60) + a + b. You have to use the rules of algebra. Since 60 is a common factor of 60a + 60b, you can FACTOR the expression (using the Distributive Property in reverse). What does that give you?
Matt had moved on to a different question, and didn’t answer this. Let’s finish.
We can factor out the 60, and then divide both sides by 60: $$60a+60b=480\\ 60(a+b)=480\\ a+b=8$$
Now this looks a lot like the first problem! We can list pairs of positive integers a and b whose sum is 8, and look for pairs for which … what? We haven’t yet used the fact that 60 is the highest common factor: If the HCF of \(60a\) and \(60b\) is 60, then a and b must have no common factors. So, in which cases do the two numbers have no common factors?
- 1, 7 – yes
- 2, 6 – no, common factor 2
- 3, 5 – yes
- 4, 4 – no, common factor 4
(We stop here, because order doesn’t matter; the pair “7, 1” is the same pair as “1, 7”.)
So the only two solutions correspond to \(a=1,b=7\) and \(a=3,b=5\). Multiplying by 60, we get \(m=60,n=420\) or \(m=180,n=300\). The first pair is Matt’s guess; the second is new. Their sum is 480, and their HCF is 60, so we’re done.