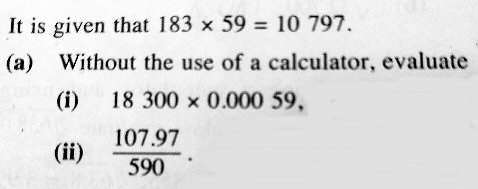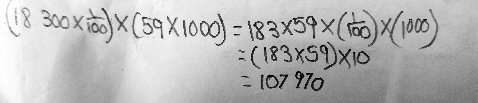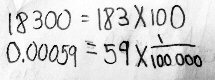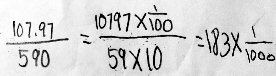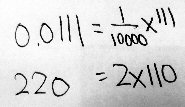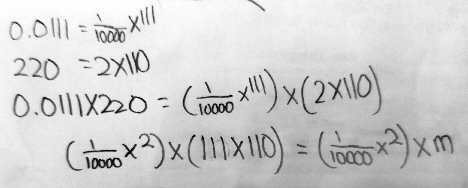(A new question of the week)
We’ve looked in the past at place values, but here we’ll see some tricks for doing multiplication and division with both decimals and large numbers by moving the decimal point around. The first question is primarily a matter of arithmetic, then the second extends it to the algebraic concept of expressing one quantity in terms of another.
Using one arithmetic fact to find others
Here is the question, from the start of June:
I haven’t done any working as I do not know how to solve this. Please guide me. Thanks.
Conrad recognizes that we want to see his work, in order to know what sort of help he needs; but it’s okay to just say you don’t know where to start! Without experience, it might be hard to figure out what he is expected to do.
By the way, Conrad is using the convention of putting spaces in a number to separate thousands (that is, groups of three digits, sometimes called periods), on both sides of the decimal point. We will sometimes use the same notation, and sometimes use commas as is more standard in America. If you are unfamiliar with this, see Decimals, Commas, Thousands, and Lakhs.
Multiplication with a decimal point
Doctor Fenton answered by giving a similar example, using the same given fact:
Hi Conrad,
The idea of this problem is that if we multiply two numbers which have the same digits as the given product, the answer must have the same digits, and the only difference will be where the decimal point is.
For example, given that 183 × 59 = 10797, then a product 18.3 × 5900 can be written as
18.3 × 5900 = (183/10) × (59*100) = (183×(1/10)) x (53 × 100)where we have divided one factor by 10 and multiplied the other factor by 100. When you multiply several numbers, you can write those factors in any order, so we can write
(183 × (1/10)) × (59 × 100) = 183 × 59 × (1/10) × 100 = (183 × 59) × (1/10 × 100) = (183 × 59) × 10,so the answer will be 10797 × 10 = 107,970 .
If you know scientific notation, the process is even simpler.
Can you find your answers by determining where to put the decimal point in the given problems?
Conrad’s age suggests that he likely has not seen scientific notation, but this problem is very closely related to how that is used in multiplication. In this example, we could say $$18.3\times 5900=(183\times 10^{-1})(59\times 10^2)=(183\times 59)(10^{-1}\times 10^2)=10\ 797\times 10^1=107\ 970$$ (In actual scientific notation, we would have written \((1.83\times 10^{1})(5.9\times 10^3)=(1.83\times 5.9)(10^{1}\times 10^3)=10.797\times 10^4\), which is not directly related to our problem as it doesn’t use the given numbers.)
We could also say that we changed \(183.\times 59.\) to \(18.3\times 5900\) by moving the decimal point one place to the left and 2 places to the right, so in the answer it moves a net distance of 1 place to the right. This is the same technique commonly used in multiplying decimals by hand: we count the decimal places in each number and add them up, using that sum to place the decimal in the result.
A wrong attempt
Conrad this time showed some work:
I tried to do part (i) after looking at your example but I don’t know what’s wrong with my working. My working is attached.
Conrad is doing some things backward, which is a natural mistake on first exposure to these ideas. We need to start with the given numbers 183 and 59 and multiply them to get 18,300 and 0.00059, rather than start by writing the numbers we want to multiply.
Doctor Fenton broke the problem down a little more:
The first problem is to find 18300 × 0.00059.
You have written (18300 × 1/100) × (59 × 1000). That is not the same product the problem asks about, since
(18300 × 1/100) × (59 × 1000) = (183) × (59000).You need to write each of the multiplicands in terms of the given numbers 183 and 59.
Can you write 18300 = 183 × ______?
You also need to write 0.00059 in the form 59 × ______. Writing decimals is somewhat tricky. Note that
59 59 59 5.9 = ---- , .59 = ----- , and .059 = ------ . 10 100 1000Can you see how to write .00059 as a quotient of 59 and some power of 10?
Putting the pieces together
Conrad this time made a good start, answering the two specific questions correctly:
I wrote it out the equation
Um I don’t understand what you meant by quotient.
What do I do next?
Multiplying 183 by 100 adds the two zeros on the end; dividing 59 by 100,000 moves the decimal point left 5 places. Both are good; but some vocabulary got in the way.
Doctor Fenton showed the next step:
A quotient is the result of a division. If I divide 18 by 3, the result is 18/3=6. In a division problem like this, 18 is called the dividend, 3 the divisor, and 6 is the quotient (of 18 divided by 3).
You have correctly written 18300 as 183 × 100, and .00059 as 59 × (1/100000), so the given problem
18300 × 0.00059becomes
(183 × 100) × (59 × (1/100000)) = (183 × 59) × (100 × 1/100000) = 10797 × (100 × 1/100000)Can you simplify this answer?
Since \(100\times\frac{1}{100\ 000} = \frac{1}{1000}\), we just have to divide \(10\ 797\) by \(1000\) to get \(10.797\).
As I suggested earlier, we can say that we changed \(183.\times 59.\) to \(18\ 300\times 0.000\ 59\) by moving the decimal point 2 places to the right and 5 places to the left, so in the answer it moves a net distance of 3 places to the left.
Turning the given product into a division
Conrad was ready to move on to the next problem:
Thanks, I solved part (i) but can you guide me in (ii)? I am not sure. Thanks.
Doctor Fenton restated that problem, which is a division rather than a multiplication:
The second part was to determine the value of 107.97/590 without using a calculator. The basic idea is the same. Since you are given that
183 × 59 = 10797 ,dividing this equation by 59 tells you that
183 = 10797/59 .In this case, you need to write
107.97 10797 × (?) (?) -------- = ------------- = 183 x ----- 590 59 × (??) (??)where “?” and “??” are numbers which are powers of 10, i.e. 10,100,1000, etc., or 1/10, 1/100, 1/1000, etc. Then you need to simplify (?)/(??).
This time we are not directly using the given multiplication fact, but transforming it into an equivalent division fact. He explained it in simple algebraic terms, dividing both sides of the equation; if Conrad had been confused by that, we could have said it differently. The fact \(183\times 59 = 10\ 797\) is “in the same fact family” as either \(10\ 797\div 183=59\) or \( 10\ 797\div 59 = 183\); the latter is the one that looks like our goal, \(107.97\div 590\).
Will Conrad understand what to do in a division? All we can do is try.
Conrad did well:
Can you check my work so I can proceed?
There’s a lot going on here. First, he correctly rewrote each number in his problem in terms of those in the given fact: \(107.97=10797\times\frac{1}{100}\) and \(590=59\times 10\). Then, in effect he split the division (in the form of a fraction) into a product of fractions: $$\frac{107.97}{590}=\frac{10797\times\frac{1}{100}}{59\times 10}=\frac{10797}{59}\times\frac{\frac{1}{100}}{10}$$ Then he carried out the division of \(\frac{1}{100}\) by \(10\): $$\frac{\frac{1}{100}}{10}=\frac{1}{100}\times\frac{1}{10}=\frac{1\times 1}{100\times 10}=\frac{1}{1000}$$ Finally, he put it all together: $$\frac{107.97}{590}=\frac{10797}{59}\times\frac{\frac{1}{100}}{10}=183\times\frac{1}{1000}=\frac{183}{1000}=0.183$$
We can also observe that in going from \(\frac{10797}{59}\) to \(\frac{107.97}{590}\) we have moved the decimal point two places to the left on top, and one place to the right on the bottom; the result is to move it two places to the left and one place to the left, for a total of three places to the left, in the answer.
Doctor Fenton approved:
That’s correct! Good work!
Once again, with variables
While that discussion was continuing, Conrad had asked another question along the same lines, but this time using a variable, and requiring a little more thinking:
I need help on this. I don’t know what to do in the first step.
Here, if we had been given the value of m, \(111\times 11=1221\), it would be almost like the problems above. But it’s using the ideas we’ve been working with to introduce something considerably more powerful. Now we are not just finding ways to avoid a calculator, but relating different values using a variable.
Doctor Rick took this one, starting with a hint for each part:
Hi, Conrad.
I have seen the other problem that you were working on with Doctor Fenton’s assistance. This problem takes the same ideas one step further.
Notice that 220 = 2 × 110. It’s easy to multiply by 2 (you shouldn’t need a calculator — in fact, you could do it using addition if necessary). So start by finding 0.0111 × 110, using the same ideas as before.
For part (b), you might think that you need to multiply or divide by 5, but if you notice that 2 × 5 = 10 (and 10 is easy to work with), you can find an easier way.
Give it a try, and let us see what you can do with these ideas.
I will admit that I assumed when I saw this that we would be bringing in a division by 5! But it’s a good idea not to make assumptions too soon, because sometimes as you work through a problem, you discover ideas that were not visible on the surface. I often see students get such an idea stuck in their minds.
Conrad replied,
I tried to link it to 111 × 11 = m but I need some help.
This is essentially how the other problems began, and is good; Conrad has learned this part well. But what comes next, when the variable comes into play?
Doctor Rick took it from there, uncertain how much algebra Conrad knows:
Let me copy the problem here for reference:
Given that 111 × 11 = m, without using calculator and using this information,
(a) find 0.0111 × 220 in terms of m,
(b) evaluate m/5.55 .
So far, you have:
0.0111 = 1/10000 × 111 220 = 2 × 110Now, I don’t know exactly what you have learned about writing mathematical expressions or about such things as commutative and associative properties. It might help if you can tell me what you have been learning – I do not recall if you told Doctor Fenton anything about this. But I will try some things and you can tell me if they are familiar to you.
For (a), we want an expression “in terms of m”. Since m = 111 × 11, we’d like to rewrite 0.0111 × 220 as 111 × 11 × (some numbers). It’s helpful to keep our goal in mind as we work.
So far, you have found that we can replace each number in 0.0111 × 220 as follows:
0.0111 × 220 becomes (1/10000 × 111) × (2 × 110)Do you see what I did here? If you have learned about changing the order and grouping of numbers in a product, then you will understand that this next version of the expression has the same value as the one above:
(1/10000 × 2) × (111 × 110)Do you notice that we are closer to what we want, but not quite there yet? What more needs to be done? Can you do it?
We have the 111, but not the 11 we need to have; when we have that, we’ll be able to replace \((111\times 11)\) with m.
Almost there
Conrad wrote back:
So I tried it and I replaced the 111×110 with m. Is this correct? Can I write the answer and decimal?
(A little detail I notice here is that Conrad has done something I often recommend to students who struggle a little with fractions: writing whole numbers at the same height as the numerators, as a reminder that, for example, \(111\) can be thought of as \(\frac{111}{1}\), so that it only multiplies the numerator of the fraction next to it. But the result here, with the multiplication represented by a cross, almost looks like \(\frac{1}{1000}x^2\) instead of \(\frac{1}{1000}\times 2\)! Conrad will soon have to stop using that multiplication symbol, once “x” becomes common in his algebra. But the problem still uses it.)
Most of this, though, is good.
Rick:
Hi, Conrad. You wrote:
So I tried it and I replaced the 111×110 with m. Is this correct?
No, that’s not correct, because the problem stated that m = 111 × 11, not 111 × 110.
But just as you wrote 0.0111 as a power of ten times 111, you can write 110 as a power of ten times 11. Keep going, you’re almost there but not done yet.
Can I write the answer and decimal?
I’m not sure what you mean here. You will be able to write the answer as a single decimal number times m, if that’s what you mean.
Finishing it off
Conrad didn’t reply; let’s finish for him:
Part (a) asks us to “find \(0.0111\times 220\) in terms of m, given that \(111\times 11 = m\)”. Conrad found that \(0.0111 = 111\times \frac{1}{10000}\). We can also go one step further than he did, and say that \(220=2\times 11\times 10\). (I’m not combining 2 and 10 for a reason.)
Now we can put it together: $$0.0111\times 220 = \left(111\times \frac{1}{10000}\right)\times\left(2\times 11\times 10\right) =\\ \left(111\times 11\right)\times 2\times\left(\frac{1}{10000}\times 10\right) =\\ m\times 2\times\left(\frac{10}{10000}\right) = \frac{2m}{1000} = \frac{m}{500}$$
Part (b) asks for \(\frac{m}{5.55}\), not in terms of m (as it already is), but just as a number. So we will be using the fact that \(111\times 11 = m\) immediately. We can also see that $$5.55 = 555\times \frac{1}{100} = 111\times 5\times \frac{1}{100}$$ Therefore, $$\frac{m}{5.55} = \frac{111\times 11}{5\times 111\times \frac{1}{100}}$$ Now, what can we do with this? We can cancel 111 from the numerator and the denominator; that gives us $$\frac{11}{5\times \frac{1}{100}}$$ Now we can multiply the numerator and denominator by 100 to eliminate the fraction in the denominator: $$\frac{11\times 100}{5}$$ Finally (I think this is the trick Doctor Rick had in mind) we can multiply the numerator and denominator by 2 to turn that 5 into a 10: $$\frac{2\times 11\times 100}{2\times 5} = \frac{22\times 100}{10} = 22\times 10 = 220$$
And in fact, since we really knew all along that \(m=1221\), we can calculate \(\frac{m}{5.55} = \frac{1221}{5.55} = 220\) with a calculator. But what we did required less actual calculation (though it took more thinking).