(A new question of the week)
It is not unusual for mathematicians to define a concept in multiple ways, which can be proved to be equivalent. One definition may lead to a theorem, which another presentation uses as the definition, from which the original definition can be proved as a theorem. Here, in yet another good question from late May, we have two different ways to “define” the number \(e=2.71828…\), a series and a limit, and a student wants to prove directly that they are equivalent. We’ll get a proof, then dig in to really understand it.
Proving two definitions are equivalent
Matthew asked:
Hi!
I’m looking for a rigorous proof that the following definitions of e are equivalent:
e = 1 + 1 + 1/2! + 1/3! + 1/4! + …
e = lim [n→∞] (1 + 1/n)^n
What I’ve done so far:
I understand that:
lim [n→∞] (1 + 1/n)^n = 1 + 1 + (1 – 1/n) 1/2! + (1 – 1/n)(1 – 2/n) 1/3! + (1 – 1/n)(1 – 2/n)(1 – 3/n) 1/4! + …
I also understand this:
lim [n→∞] (1 – 1/n)(1 – 2/n)(1 – 3/n) = 1 x 1 x 1 = 1
And so if we take a fixed value m (with m as a natural number):
lim [n→∞] 1 + 1 + (1 – 1/n) 1/2! + (1 – 1/n)(1 – 2/n) 1/3! + (1 – 1/n)(1 – 2/n)(1 – 3/n) 1/4! + … + (1 – 1/n)(1 – 2/n)(1 – 3/n)…(1 – (m – 1)/n) 1/m!
is equivalent to:
1 + 1 + 1/2! + 1/3! + 1/4! + … + 1/m!
But I then get stuck on the next step. I only understand the ‘equivalence’ where the series terminates at a fixed natural number (in this case m). How do I make the transition to proving it for the infinite series, where the number of members of the series approaches infinity, whilst n also approaches infinity within each element of the series?
I’m in particular looking for a rigorous proof, where the two sequences are named t_n and s_n.
So that for every epsilon there exists a number N so that for every n > N then |t_n – s_n| < epsilon.
Really grateful for any help on this!
Matthew knows how to ask a question: He has clearly stated what he wants to do, and shown a good bit of work, including where the difficulty lies. But we’ll need to get up to speed to make sure we understand the question, as well as this initial work!
What we need to prove
The two “definitions” are quite different, one a series, the other a limit. Here is how Wikipedia introduces its article on e:
The number e, also known as Euler’s number, is a mathematical constant approximately equal to 2.71828, and can be characterized in many ways. It is the base of the natural logarithm. It is the limit of \(\left(1+\frac{1}{n}\right)^n\) as n approaches infinity, an expression that arises in the study of compound interest. It can also be calculated as the sum of the infinite series
$$e=\sum_{n=0}^{\infty }{\frac {1}{n!}}=1+{\frac {1}{1}}+{\frac {1}{1\cdot 2}}+{\frac {1}{1\cdot 2\cdot 3}}+\cdots $$
That is, they take the limit as the actual definition, and present the series as a way to calculate it. Here is a table of the first 11 terms of the series and its sums:
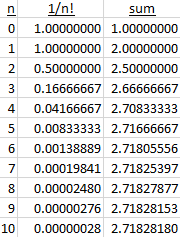
We have already reached 8 significant digits of accuracy.
Here is a table of the first 11 values of the limit:
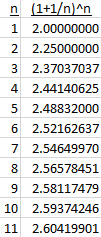
We don’t even have one significant digit yet!
In fact, if we make the limit move exponentially faster, by using \(2^n\) in place of n, it is still slow to converge:
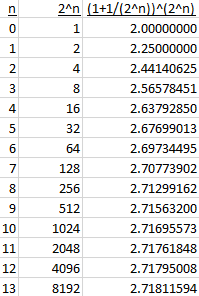
It takes 8 thousand “steps” to get 4 significant digits! (Of course, in principle we only need to do this calculation once, rather than summing terms, so it is not that inefficient to calculate, apart from the efficiency of using a very large exponent in the first place, and deciding what value to use.)
But they do approach the same limit. How can we prove it?
What he’s done so far
Let’s look at what Matthew did, which he didn’t fully explain.
First, he said $$\lim_{n\to\infty} \left(1 + \frac{1}{n}\right)^n = 1 + 1 + \left(1 – \frac{1}{n}\right) \frac{1}{2!} + \left(1 – \frac{1}{n}\right)\left(1 – \frac{2}{n}\right) \frac{1}{3!} + \left(1 – \frac{1}{n}\right)\left(1 – \frac{2}{n}\right)\left(1 – \frac{3}{n}\right) \frac{1}{4!} + \cdots$$
Where did that come from? He has applied the binomial theorem to \(\left(1 + \frac{1}{n}\right)^n\); this theorem in general says that $$(1+x)^n = \sum_{k=0}^n {_nC_k}x^k$$
The kth term of this sum (starting with the 0th) is $${_nC_k}\left(\frac{1}{n}\right)^k = \frac{n!}{k!(n-k)!}\frac{1}{n^k} =$$ $$\frac{n(n-1)(n-2)\cdots(n-k+2)(n-k+1)}{n^k}\frac{1}{k!} =$$ $$\frac{n}{n}\cdot\frac{n-1}{n}\cdot\frac{n-2}{n}\cdots\frac{n-k+2}{n}\cdot\frac{n-k+1}{n}\frac{1}{k!} =$$ $$\left(1-\frac{0}{n}\right)\left(1-\frac{1}{n}\right)\left(1-\frac{2}{n}\right)\cdots\left(1-\frac{k-2}{n}\right)\left(1-\frac{k-1}{n}\right)\frac{1}{k!}$$
which agrees with what he wrote; observe that for \(k=0\) the term has zero factors, and is simply 1; for \(k=1\), it is just the one factor \(\left(\frac{n}{n}\right) = 1\). That’s why Matt has written the first two terms as mere numbers (and will continue doing so): for clarity.
His calling this the limit, however, is premature, because n is still a variable. This is the tricky part.
The proof
Doctor Fenton answered, starting his proof the same way but being more careful with limits:
I recalled a discussion of this in an old classic, Richard Courant’s Calculus textbook.
Let Tn denote the n-th partial sum of the series \(\sum_{k=0}^\infty\frac{1}{k!}\) , so \(T_n=\sum_{k=0}^n\frac{1}{k!}\),
and let Sn denote \((1+\frac{1}{n})^n\) .
By the Binomial Theorem,
$$S_n= \sum_{k=0}^n {_nC_k}\frac{1}{n^k}= \sum_{k=0}^n \frac{n!}{k!(n-k)!}\frac{1}{n^k}= \sum_{k=0}^n \frac{1}{k!}\left(1-\frac{1}{n}\right)\left(1-\frac{2}{n}\right)\cdots\left(1-\frac{k-1}{n}\right)$$
Clearly, Sn ≤ Tn, since each term in Tn is multiplied by a product of factors, each less than 1, to obtain the corresponding term of Sn.
Also, notice that both sequences are increasing and bounded, so each converges. Let
\(S=\lim_{n\to\infty} S_n\) .
If m < n, then the sum $$\sum_{k=0}^m \frac{1}{k!}\left(1-\frac{1}{n}\right)\left(1-\frac{2}{n}\right)\cdots\left(1-\frac{m-1}{n}\right)\lt S_n$$
since Sn has additional non-negative terms added. If we take the limit as n→∞, the left side approaches Tm , while the right side approaches the limit S. Then we have that Tm ≤ S, so Sm ≤ Tm ≤ S.
Now, taking the limit as m→∞ gives S = T, so the two limits are the same.
There’s a typo in that summation, which I can’t remove because it figures into the discussion; don’t worry if you find it.
Fixing an error
Matthew replied, catching that error and helping us out in the process:
Hi, thanks so much for your quick answer. I think I’m getting closer but there’s still some things I’m not getting.
I think when you wrote $$\sum_{k=0}^m \frac{1}{k!}\left(1-\frac{1}{n}\right)\left(1-\frac{2}{n}\right)\cdots\left(1-\frac{m-1}{n}\right)\lt S_n$$
you must have meant: $$\sum_{k=0}^m \frac{1}{k!}\left(1-\frac{1}{n}\right)\left(1-\frac{2}{n}\right)\cdots\left(1-\frac{k-1}{n}\right)\lt S_n$$
Or maybe: $$1+1+\sum_{k=2}^m \frac{1}{k!}\left(1-\frac{1}{n}\right)\left(1-\frac{2}{n}\right)\cdots\left(1-\frac{k-1}{n}\right)\lt S_n$$
If I expand this last series on the left I get:
1 +
1 +
(1/2!){1-1/n} +
(1/3!){(1-1/n)(1-2/n)} +
… +
(1/m!) {(1-1/n)(1-2/n)…(1-(m-1)/n)}
So then Sn has all these terms, but some additional terms added.
Am I making sense? Sorry if I’ve got this confused somewhere!
Thanks again!
The “or maybe” is really the same summation, with the first two terms stated explicitly as we saw before.
Clarifying the limit
Doctor Fenton confirmed his correction, and added some notation to make the details easier to talk about:
You are correct. I was hurrying to get ready for a meeting and typed m instead of k.
The idea is to take a sum of a fixed number m of terms from Sn, so that the partial sum Sn is larger than the sum of its first m terms.
Call this sum Sn,m , so Sn,m < Sn , and as n→∞, Sn,m→Tm while Sn→S, giving Tm ≤ S. Then Tm is squeezed between Sm and S.
Sorry to put you to so much work over a typo.
That is, we are defining $$S_{n,m} = \sum_{k=0}^m \frac{1}{k!}\left(1-\frac{1}{n}\right)\left(1-\frac{2}{n}\right)\cdots\left(1-\frac{k-1}{n}\right)$$ and \(S_{n,m}< S_n\) for all n, for any given m, so, taking the limit on each side, \(T_m\le S\). Giving a name to the sum of only m terms of the sum for n makes it easier to talk precisely about what we are doing.
Matthew wrote back, nicely stating what he did and did not understand:
Hi there, many thanks for your further response and for clarifying.
I think I now understand the proof in general terms but I’m not sure I fully understand all the details. In particular I’m not clear exactly how it follows that Tm < S.
We have the following inequalities:
Sn,m < Sn for all values of n (as Sn always includes additional non-negative terms)
Sn < S for all values of n (as Sn is monotonically increasing, approaching the limit S)
Sn,m < Tm for all values of n (as Sn,m contains the same terms as Tm terms except with further positive coefficients less than 1)
I’m not sure I can get from these inequalities that Tm < S
But maybe if Sn,m approaches the limit of Tm as n→∞, and Sn,m remains less than Sn without approaching the limit of Sn, then I think it would follow that Tm is less than Sn.
And the I think the rest would follow as m → ∞, as Tm is ‘squeezed’ between Sm and S. i.e. Sm < Tm < S, and Sm → S as m → ∞.
I’m not sure how I can show that Sn,m does not approach the limit of Sn as m → ∞, although it seems highly intuitive to assume it does not.
Again, hope I’m making sense and not getting mixed up, or if I’m missing something obvious.
Thanks again!
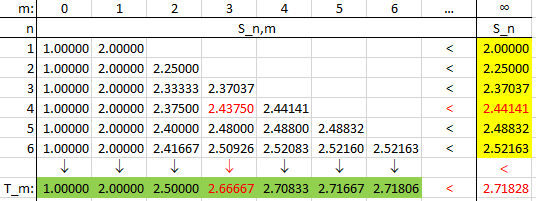
It can be helpful to look at some actual numbers. Here is a table of values of our \(S_{n,m}\) showing the inequalities Matt points out:
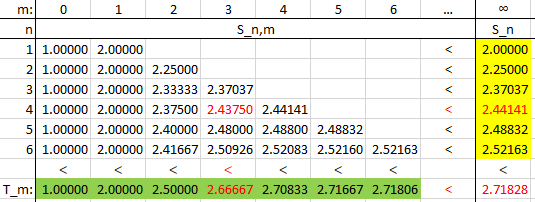
I have highlighted \(S_{4,3} = 2.43750\); we can see that
- \(S_{4,3} = 2.43750 < S_4 = 2.44141\)
- \(S_4 = 2.44141 < S = 2.71828\)
- \(S_{4,3} = 2.43750 < T_3 = 2.66667\)
But these inequalities in themselves don’t lead us to the conclusion that \(T_m\) and \(S_n\) have the same limit.
Doctor Fenton showed the missing link:
You write
I’m not sure I can get from these inequalities that Tm < S.
But maybe if Sn,m approaches the limit of Tm as n→∞ and Sn,m remains less than Sn without approaching the limit of Sn, then I think it would follow that Tm is less than Sn
That’s exactly correct. Sn,m is the sum of the first m terms of Sn, and in this part of the argument, m is fixed.
Sn,m = 1 + (1/1!) + (1/2!)(1-1/n) + … + (1/m!)(1-1/n)(1-2/n)⋅⋅⋅(1-(m-1)/n)
while
Sn = 1 + 1/1! + (1/2!)(1-1/n) + … + (1/n!)(1-1/n)(1-2/n)⋅⋅⋅(1-(n-1)/n) .
Sn,m always has m terms, a fixed number, while the number of terms in Sn increases without bound. As n→∞, each term (1-k/n)→1, so the kth term of Sn,m approaches 1/k!, i.e. lim(n→∞) Sn,m = Tm . But the number of terms in Sn keeps increasing, so that Sn approaches S, which turns out to be T = e.
His table would differ in just one point, taking the limit of each column rather than just an inequality:
The fact that we are holding m fixed and then letting n vary gives us a grip on the limits.
Final thoughts
Matthew now worked out the final bit:
Hi – thanks for your encouraging response.
I’ve been wrestling with this part of the proof:
“If m < n, then the sum $$\sum_{k=0}^m \frac{1}{k!}\left(1-\frac{1}{n}\right)\left(1-\frac{2}{n}\right)\cdots\left(1-\frac{m-1}{n}\right)\lt S_n$$
If we take the limit as n→∞, the left side approaches Tm , while the right side approaches the limit S. Then we have that Tm ≤ S”
I think I’ve got it now!
If I say an < bn for all n, and say as n→∞ then an→a, and bn→b,
then it follows that a ≤ b.
For if no member of the series of an is greater than any member of the series bn, then it is not possible that a > b.
But it is possible that a = b, as it could be that bn – an→0 as n→∞.
And it is possible that a < b as it could be that (lim n→0 bn – an) > 0.
Hence a ≤ b.
So replace an with Sn,m and bn with Sn, then given that Sn,m→Tm and Sn→S when n→∞ and Sn,m < Sn for all n it follows that Tm ≤ S.
And the rest follows!
So think I’m home and dry with this one! ? (assuming my above reasoning is correct … ?)
Thanks again for taking the time to read and respond.
Well explained! If \(a_n\to a\), \(b_n\to b\), and \(a_n<b_n\) for all n, we can’t be sure that \(a<b\), but we do know that \(a\le b\).
Doctor Fenton agreed:
That’s correct!
So we have the proof.
