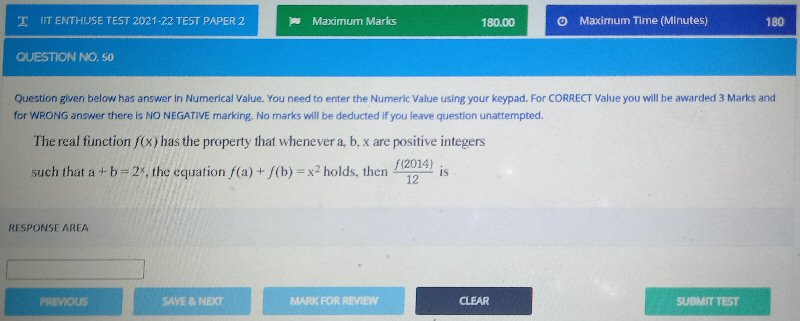
(A new question of the week)
May was a particularly good month for interesting questions! Here is one requiring us to find one value of a function, based on an unusual property: If \(a+b=2^x\), then \(f(a)+f(b)=x^2\). The problem turned out to be not as hard as it looked, yet the function itself is quite interesting when we step back to look at the whole thing. We’ll see a couple valuable strategies for solving unfamiliar, non-routine problems along the way.
A test question
The question came from Manas in late May:
I cannot make use of the given data:
This posed a problem for me, as we do not help students cheat on tests. Too often, students just attach a PDF of a test and, in effect, say “Do this test for me so I can get the credit”. (We politely refuse, and in more egregious cases may try to notify the instructor.) This was not quite like that, so I gave Manas the benefit of the doubt, giving just the most basic hint along with a warning:
Hi, Manas.
First, this is clearly a test for which you want to get credit, so I can’t come close to giving you the answer without cheating for you. (We sometimes report attempts at cheating.)
All I will say is the very first thing I thought of when I saw the problem: What is the next power of 2 greater than 2014? I was able to quickly solve it starting from there.
Clearly the problem is intended to elicit some creative thinking, as it is far from routine. So my goal was to get Manas to think for himself, with a minimal nudge.
Manas replied:
Yes it was of test, I posted it after the test.
I found that next power of 2 is 2048 and 2014 can be written as 2048 – (2⁵ + 2¹).
But that was all I could do.
I also tried to write 2^x + x² = 2014 (by guess work) don’t know if it’s the correct way.
(I can also share a proof that I posted it after the test by attaching a screenshot of paper timings.)
Manas has gone a little beyond my question, showing good initiative; but has perhaps gone a little too fast. Trying even random things can sometimes be fruitful, especially when you have no good ideas! But it would be more helpful to directly relate what we are seeing to the form of the statements in the problem; since it talks about \(a+b=2^x\), we want to see something like \(2014+34 = 2^{11}\) (the sum of 2014 and another number equaling a power of 2). Writing 34 as \(2^5+2^1\) (effectively, in binary) seems potentially useful, breaking it down into a series of powers of 2, but it’s probably better to take smaller steps. The form \(2^x+x^2=2014\) is probably irrelevant, since we want \(f(a)+f(b)=x^2\), which relates the value of the function, not its inputs, to a square.
I could have asked for the offered evidence of ethical behavior, but by this time is was more than three hours after the initial question, so I could be sure the 180 minute test was not still current, regardless. (And now it’s over two months later, so I hope it’s safe to be publishing an answer.) So I continued with hints, showing the relevant form:
Nothing in the problem is about the sum of two powers of 2, or about the sum of a power of 2 and a second power, so I don’t think your ideas lead in a useful direction (though trying anything can be of use, because we don’t always see all the implications!).
You found that 2014 = 2048 – 34, so 2014 + 34 = 2^11. What does that tell you about f(2014)?
Now, how might you find f(34)?
My strategy at this point is just to do whatever I can do, taking one step at a time without being sure what comes next; but in doing so, I observe that I’ve reduced the original problem to a similar problem with a smaller number. That seems like progress. Maybe the problem will be recursive?
Manas wasn’t yet ready to proceed:
Thank you for helping and replying till now.
Even with this hint I am still not able to crack it.
It’s much more helpful when you show some actual attempt, even if it went nowhere, than just to say that whatever you tried went nowhere – it’s what you do, more than whether it worked, that shows us how how we can best help.
Two possible strategies
I gave a more direct hint:
Can you show me what you tried using my hint?
Here is what I said:
You found that 2014 = 2048 – 34, so 2014 + 34 = 2^11. What does that tell you about f(2014)?
Do you see that 2014 + 34 = 2^11 implies that f(2014) + f(34) = 11^2 ? So if you can find f(34), you can find f(2014).
Repeat the same thinking for the number 34, hoping to get f(34) in terms of smaller numbers.
Another direction you could think is to try letting a and b be various small numbers (e.g. 1 and 1, 1 and 2, etc.) to see if you can find the function value for some small numbers. (If they weren’t required to be positive, I would try zeros.)
We’ll be following the first suggestion; but first, let’s look at what I had in mind in that last paragraph.
Playing with small numbers: Bottom-up
Often when I see a functional equation, I start by plugging in small numbers to see what will happen. Some possibilities here (pairs of positive integers whose sum is a power of 2) are
$$a+b=2^x\;\Rightarrow\; f(a)+f(b)=x^2$$
$$1+1=2=2^1\;\Rightarrow\; f(1)+f(1)=1^2=1\;\Rightarrow\; 2f(1)=1\;\Rightarrow\; f(1) = \frac{1}{2}$$
$$2+2=4=2^2\;\Rightarrow\; f(2)+f(2)=2^2=4\;\Rightarrow\; 2f(2)=4\;\Rightarrow\; f(2) = \frac{4}{2} = 2$$
$$1+3=4=2^2\;\Rightarrow\; f(1)+f(3)=2^2=4\;\Rightarrow\; f(3) = 4-f(1) = 4-\frac{1}{2}=\frac{7}{2}$$
This doesn’t seem to be leading to a nice pattern we can generalize, so this “bottom-up” strategy by itself doesn’t look like it will give us a quick answer. But we’ll get back to this, after spending some time with the other strategy!
Starting with the given number: Top-down
Manas made some progress by starting with 2014:
Yes I tried it out later on till I reached till f(2).
Now closest power of 2 for f(2) would be 1.
So a = 0 and b = 2.
However I could not get a definite value which would help me to solve f(2014)+ f(34).
The last equation was f(0) + f(2) = 2¹.
This is excellent until the point where he is stuck. Let’s work through the details so far:
We are told that $$\text{if } a+b=2^x\text{, then }f(a)+f(b)=x^2$$ We want to find \(f(2014)\), so we let \(a=2014\) and \(b = 34\), and conclude that $$\text{since } 2014+34=2048=2^{11}\text{, then }f(2014)+f(34)=11^2$$ Therefore \(f(2014) = 121-f(34)\).
So now we want to find \(f(34)\). We find that the next power of 2 greater than 34 is \(64=2^6\).
Now we repeat: Let \(a=34\) and \(b = 30\), and conclude that $$\text{since } 34+30=64=2^6\text{, then }f(34)+f(30)=6^2$$ Therefore \(f(34) = 36-f(30)\).
That didn’t take us much farther, but we’ve crossed over another power of 2. To find \(f(30)\), we see that the power of 2 greater than 30 is \(32=2^5\).
Now we repeat again: Let \(a=30\) and \(b = 2\), and conclude that $$\text{since } 30+2=32=2^5\text{, then }f(30)+f(2)=5^2$$ Therefore \(f(30) = 25-f(2)\).
But 2 is itself a power of 2; and we aren’t allowed to take \(b=0\). So we’re stuck. We need a new strategy.
(Actually, since I showed the bottom-up strategy above, you may notice we’ve already discovered what to do!)
Changing strategy … and success!
I gave another hint:
The technique does have to change a little to find f(2). (Note that you can’t use 0, as I mentioned.)
What does f(2) + f(2) equal?
(This is where playing with small numbers might have been helpful, because you might have discovered this before getting into the routine of working from large to small numbers.)
Having played with small numbers myself, I knew what to suggest this time! But notice that the change needed here was merely to avoid zero by popping back up to the next higher power of 2, making the sum 4.
That was enough. Manas answered,
Thank you for your help I was able to crack it and the answer which came was 9.
I solved using the last hint you gave which helped me to find f(2) which came equal to 2.
I used this value to find f(30) thus finally solving for f(2014) which came equal to 108 .
Once again thank you sir.
As we found above, \(f(2) = 2\). So we can put everything together:
$$f(2014) = 121-f(34)\\ f(34) = 36-f(30)\\ f(30) = 25-f(2)\\ f(2) = 2$$ so $$f(30) = 25-f(2) = 25-2=23\\ f(34) = 36-f(30) = 36-23 = 13\\ f(2014) = 121-f(34) = 121-13 = 108$$
We were asked for $$\frac{f(2014)}{12} = \frac{108}{12} = 9$$
Exploring further
I acknowledged the correct answer, and suggested a further step:
Perfect!
Fun problem, isn’t it? Now, I wonder if we could find f(x) for all positive integers?
The last step in problem solving, as I express it, is to look back (checking your answer, and looking for alternative methods), look around (seeing if the problem suggests any interesting extensions), and look ahead (thinking about how you might use what you learned for future problems). That’s what I’m doing here.
Manas gave the kind of response I hoped for, showing interest beyond answering the one problem:
Yes we can find f(x) for all positive integers by the same mechanism.
We only require values of principle functions (here) f(1), f(3), f(5) and f(7) if required.
Cause rest all numbers eventually break down to ‘something’ + f(1)/f(3)/f(5).
If we have to find f(3), then it can be written as
3+1=2²
f(3)+f(1)=2²
f(1)=1/2
Thus we can find f(3) and for all positive integers.
I’m not sure of the significance of 1, 3, 5, 7; but it is true that we will always come down to some special case in a small number, as we saw above in “playing” with them. But what’s he’s done is to suggest an existence proof, that the function is in fact defined for all positive integers.
Not wanting to get too deep into this question unless Manas chose to, I concluded:
Yes, I think it could be done; perhaps it would even be possible to make a formula for it.
Of course, we don’t need to do it; you’ve solved the problem as stated.
What does the function look like?
But let’s go ahead and look into it.
We found two cases, depending on whether a is a power of 2 or not.
If it is, then \(a = 2^n\) and $$a+b=2^x\;\Rightarrow\; f(a)+f(b)=x^2\\ 2^n+2^n=2^{n+1}\;\Rightarrow\; f(2^n)+f(2^n)=(n+1)^2\\ f(2^n)=(n+1)^2/2$$
Otherwise, let \(n= \lceil \log_2(a)\rceil\), where the special symbols represent the ceiling function (rounding up), and we have a recursive formula, $$a+b=2^n\;\Rightarrow\; f(a)+f(b)=n^2\\ f(a)=n^2-f(2^n-a)$$ where \(0\lt b=2^n-a\lt a\), because \(2^{n-1}\lt a \lt 2^n\). This recursion will always terminate, so we know we can evaluate the function for any positive integer.
Putting this together, we have a piecewise function: $$\text{Let }n=\lceil\log_2(a)\rceil$$
$$f(a)=\left\{\begin{matrix} \frac{(n+1)^2}{2} & \text{if }a=2^n \\ n^2-f(2^n-a) & \text{otherwise} \end{matrix}\right.$$
I made a spreadsheet to evaluate this; here are the first 32 rows:

The graph (for a through 2048, here) looks very interesting:
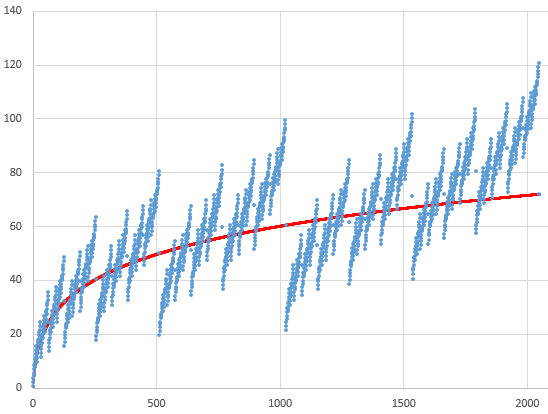
The red line is \(f(x) = \frac{1}{2}\left(\log_2(x)+1\right)^2\), which passes through the points for powers of 2. (And, yes, the spreadsheet shows that \(f(2014) = 108\).) In fact, it looks rather like a fractal; here we zoom in to the part of the graph through 512, the first quarter of the graph above:
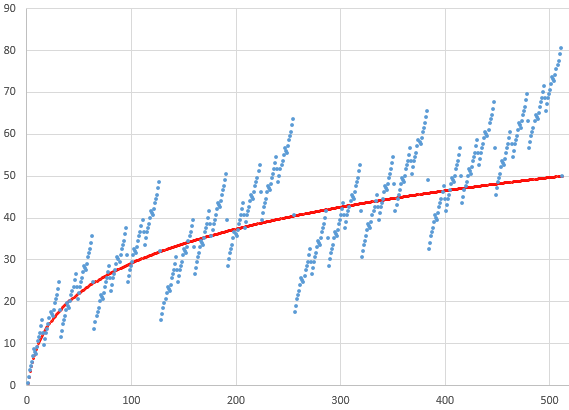
I don’t think there will be a nice closed formula for f. But it may turn out to be expressible in terms of the binary digits of the input. Maybe a reader would like to pursue that.