We’ve looked at the basics of logs and how they work; now we have some questions testing the limits of the definition. We’ll focus on the inverse idea of exponential functions with a negative base, looking at this from several perspectives.
Restrictions in the definition of a log
We’ll start with a broader question, from 2001:
Definition of Logarithm In the definition of logarithm, there are some conditions for the base. a^x = b iff x = log_a(b) where a > 0, a <> 1 (a is not equal to 1), and b > 0. Why stipulate these conditions? If they are not assumed, are there any problems or contradictions that arise? I want to know why mathematicians defined logarithm this way.
We omitted such details in introducing logs, but these restrictions will be stated in any good textbook. Here is an example of such a definition (using different variables):
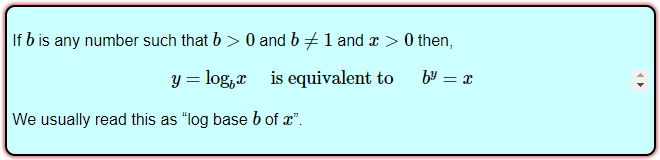
I answered, considering each of the three restrictions in turn:
What if the argument isn’t positive?
Thanks for writing to Dr. Math.
Let's just think about what happens if we violate any of these conditions.
First, if b <= 0, then we are trying to solve:
a^x <= 0
You will find that there is no solution; x must be "negatively infinite" even to produce 0, and there is no real number x for which a^x < 0 if a > 0.
The range of an exponential function consists of only positive numbers, as we can see from the graph of \(y=10^x\):
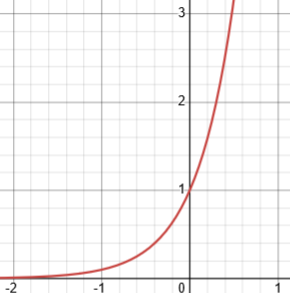
This restricts the domain of the logarithm, which we can see in the graph of \(y=\log_{10}(x)\):
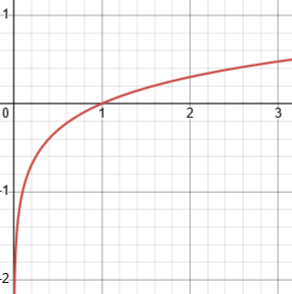
What if the base is 1?
Next, if a = 1, we are trying to solve:
1^x = b
Since 1^x = 1 for all x, this has no solution unless b = 1. So it makes no sense to talk about a logarithm with base 1.
Here are the graphs of \(y=1^x\) and \(y=\log_1(x)\) (actually \(x=1^y\), since Desmos doesn’t handle logs with base 1): 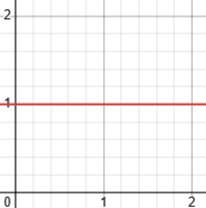
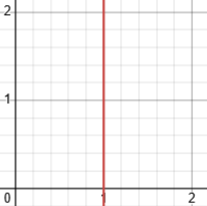
We can only take the log of 1, and then it doesn’t have a single value: \(\log_1(1)\) is indeterminate. Not very useful!
What if the base is 0?
Now, if a = 0, we have:
0^x = b
and again, there is no solution unless b = 0. This is likewise useless.
Here are the graphs of \(y=0^x\) and \(y=\log_0(x)\) (that is, \(x=0^y\)):
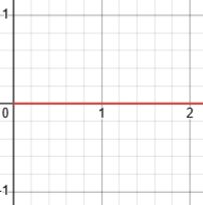
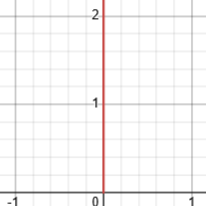
Again, the log exists only for \(x=0\), and then is equal to any (positive) number. We can’t define this as a function either.
What if the base is negative?
Finally, if a < 0, things get tricky. We can define integral powers of a (which will be positive for even x and negative for odd x); but what about fractional powers? a^(1/2) is undefined (or rather, imaginary) when a is negative. If the powers are not defined for a negative base, then logarithms are not defined either!
We’ll dig into this below. It gets even more complicated than I’ve described.
As you can see, the restrictions you asked about merely keep us from talking about logarithms when they don't make any sense. BUT ... In the first and last cases, you'll notice I mentioned real and imaginary numbers. The fact is, your definition is valid only when we are considering only real numbers. We can extend the logarithm to apply to complex numbers, and then some of these restrictions can be relaxed. You can read about complex logs and some of the complications they introduce in the Dr. Math archives: The Log of a Negative Number http://mathforum.org/dr.math/problems/witty3.27.98.html Log of Complex Number http://mathforum.org/dr.math/problems/langlands.9.15.96.html
The rest of this post will look into the question of negative bases, focusing on the exponential function; next time we’ll look at these further issues when we allow complex numbers.
Exponential with a negative base: basics
This question, from later in 2001, turns our attention to exponential functions:
Base of an Exponential Function Why can't the base of an exponential function be negative?
Doctor Rob answered, starting with positive bases for comparison:
Positive bases
Thanks for writing to Ask Dr. Math, Stefanie. Excellent question!! Let's start by looking at things like 64^(1/2). This is a square root of 64. There are two of these square roots, -8 and +8. We want the expression to represent just one of these two, and we pick the positive one, which we call the "principal value" of the square root. Thus 64^(1/2) = 8.
Recall that \(a^{1/2}=\sqrt{a}\) because $$\left(a^{1/2}\right)^2=a^{(1/2)\cdot2}=a^1=a=\left(\sqrt{a}\right)^2$$ See Squares, Roots, and Negative Numbers for details.
And just as we define \(\sqrt{x}\) as the non-negative square root (just the one principal value, rather than both at once) in order to make it a function, we do the same for the fractional power.
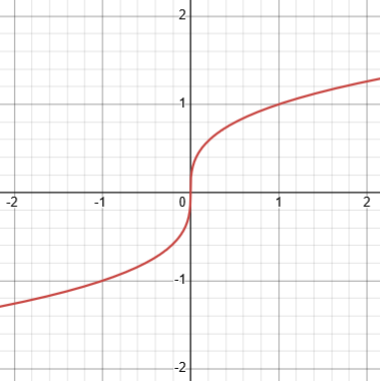
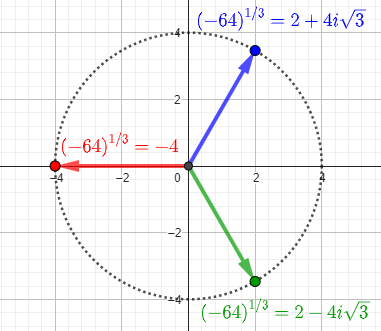
When we look at 64^(1/3), this is a cube root of 64. There are three of these cube roots: 4, -2+2*sqrt(3)*i, and -2-2*sqrt(3)*i. Notice that two of these are complex numbers. For a principal value, naturally we pick the positive one. When we stick to positive bases, we always have a positive principal value we can use, even when the exponent is an irrational real number. Furthermore, the function you get from the reals to the positive reals turns out to have no jumps or other problem points, and to have a smooth graph (the technical terms are "continuous" and "differentiable").
Here is the graph of the cube root of x, \(x^{1/3}\) you can draw it by moving your pencil smoothly from one point to another:
Negative bases
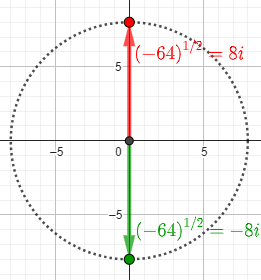
When the base is negative and the exponent is rational with an odd denominator, like (-64)^(1/3), there is a negative real number -4 which can be chosen to be the principal value. When the base is negative and the exponent is rational with an even denominator, there is no real root. For (-64)^(1/2), you have the two complex roots 8*i and -8*i. It is not clear which of these, if either, you can or should choose for the principal value. When the base is negative and the exponent is irrational, you will also not have any real root, and no clear choice for the principal value. Furthermore, there are problems making these choices in such a way that the function resulting, mapping the reals into the complex numbers, is continuous and differentiable.
Here are the three cube roots of -64:
Here are the two square roots of -64:
The ideas used here are covered in Euler’s Formula: Complex Numbers as Exponents, and in Powers of Roots and Roots of Powers.
We’ll look into irrational exponents below.
As a result of these considerations, it is very clear that it is a good idea to restrict one's attention to exponential functions with positive bases, and avoid the difficulties encountered with negative ones.
So we can calculate particular powers of negative bases, but as a function of a real variable, they don’t have the properties we want for functions (particularly in calculus: changing smoothly as we vary the exponent), and so are not useful for those purposes.
Can we define irrational powers of a negative base?
Here’s a long question from 2011, taking it further:
Raising a Negative to an Irrational Power? It Depends Dear Dr. Math, Hi, my name is Nick. I am a 10th grader attending Lake Central High School. I do things most other normal kids don't. I seem to rather enjoy math a little too much. I can understand many restrictions and rules in functions and stuff, but I came across a strange question that none of my math teachers could answer -- and it still gets me. The question is as follows: "When taking a function to an irrational power, the negative set is excluded even though the possibility of finding a positive number to an irrational power IS possible. Why is finding a negative to an irrational power not?" I have asked this to all of my teachers and my father (they are the best for my math answers) and even other relatives (though they're not really any help) -- but no one has had a clear answer. So, Dr. Math, why can't you find a value for a negative number raised to an irrational exponent? Or maybe you can; does it deal with logarithmic functions? Please try it. For example, type this on your calculator and see what you get: (-3)^(sqrt3) I seem to continue to get "Error"; and when writing it out, I am stuck. This is not only for the square root of three as an exponent, but other irrationals, such (-3)^e, and imaginaries, such as (-3)^i. I know i is the square root of (-1), but these all seem to not have any real value, so I am just truly baffled. Please, don't discard this request.
My TI-30X IIS reports “Domain error” when I enter (-3)^√(3), but correctly finds \((-3)^\frac{1}{3}=-1.44224957\) and \((3)^\sqrt{3}=6.704991854\). so “negative^rational” and “positive^irrational” work (at least sometimes), but “negative^irrational” does not. My Casio fx-115ES PLUS is similar.
Doctor Vogler answered:
Hi Nick,
Thanks for writing to Dr. Math. I enjoy math more than other adults do, too, and I am proud of that fact.
There are a number of different ways to approach your question. There is some discussion of this issue at
Base of an Exponential Function
http://mathforum.org/library/drmath/view/55604.html
Graph of y = (-n)^x
http://mathforum.org/library/drmath/view/66708.html
Why Is (-n)^fractional Invalid?
http://mathforum.org/library/drmath/view/62979.html
y to the x Power
http://mathforum.org/library/drmath/view/63367.html
The links are to our second question above, the question we’ll close with below, one that I considered for this post but couldn’t fit, and another that covers similar ideas.
Three ways to define x^y
Basically, it all comes down to: What do you mean when you write an expression like x^y? The first definition of exponents you have likely seen was the algebraic definition, where you define x^n for positive integers n as x times itself n times, then x^(1/n) as a number y such that y^n = x, and x^(p/q) as (x^p)^(1/q). You might have even seen x^y for irrational numbers y defined as a limit (if you've encountered limits; they are usually introduced in calculus or pre-calculus). In this setting, negative numbers to irrational exponents are not defined because the limit I spoke of generally does not exist; when it does, it depends on the choice of sequence approaching y.
As he says, we first define positive integer powers, $$3^4=3\cdot3\cdot3\cdot3=81,$$ then negative integer and zero powers, $$3^0=1,\\3^{-4}=\frac{1}{3^4}=\frac{1}{81}\approx0.012345679\dots,$$ then fractional powers, $$3^{\frac{3}{4}}=\sqrt[4]{3^3},$$ and then real (irrational) powers, so that $$3^\pi=3^{3.14159\dots}\approx31.544,$$ which we approach as the exponent approaches \(\pi\): $$3^3=27,3^{3.1}\approx30.135,3^{3.14}\approx30.489,\dots$$
This idea is discussed from a variety of perspectives in What Do Exponents Mean?
But, as we’ve seen, this doesn’t consistently work for negative bases.
A different way to define exponents uses calculus and first defines the natural logarithm ln(x) as an integral, or exp(x) (also written e^x) with a differential equation, and the other as the inverse function. In this context, x^y = exp(y*ln(x)) But then you have the problem that the integral for ln(x) is only defined when x is positive, so this definition only works when the base x is positive.
Different textbooks can take different approaches to these equivalent definitions:
- One is to define $$\ln(x)=\int_1^x\frac{1}{t}dt,$$ and then define \(e^x\) as the inverse function, so that $$e^x=y\text{ when }x=\ln(y).$$
- The other is to define \(e^x\) as the function for which $$\frac{d}{dx}f(x)=f(x)\text{ and }f(0)=1,$$ and then define \(\ln(x)\) as the inverse function, so that $$\ln(x)=y\text{ when }x=e^y.$$
But by either of these definitions, we can’t define \(x^y\) for negative x because we can’t define \(\ln(x)\).
A third way uses complex analysis and imaginary numbers, where the function exp(x) can be defined for complex numbers. But then exp(x) has many inverses, so the natural logarithm ln(x) is a multi-valued function. Lucky for us, exp(y*ln(x)) is always the same, no matter which value you pick for ln(x), as long as y is an integer. But if y is rational, then different choices of ln(x) will give different values for x^y, and the number of different values you can get is equal to the denominator of y.
We’ll be looking at multivalued logarithms (and powers) in more detail another time, but we’ve touched on it just enough here to see some of the complexity.
For example, the four values for 1^(1/4) are 1, -1, i, and -i. When y is irrational, then there are infinitely many different values for x^y. If x is a positive real number, and y is a real irrational number, then exactly one of those infinitely many different values for x^y is a real number. But if x is a negative real number, and y is a real irrational number, then none of those infinitely many different values for x^y is a real number; all of them are complex numbers.
My impression has generally been that calculators would evaluate powers of any base using the natural log: \(a^b=\left(e^{\ln(a)}\right)^b=e^{b\ln(a)}\), in order to use their logarithm algorithm. But that can only be done for positive bases, so they would just call a negative base an error.
On the other hand, as we’ve seen, a calculator should be able to calculate some rational powers of a negative base, such as \((-64)^{1/3}\); both my TI 30X IIS and my Casio fx-115ES Plus can handle that; clearly they don’t rely on logarithms.
On the other hand, a calculator that can handle complex numbers probably uses polar form, and does whatever it can to obtain a single value. This is discussed in
x^x, Discrepantly
Graphing an exponential with a negative base
This is from 2005:
Graph of y = (-n)^x I am curious as to what the graph of y = (-n)^(x) would look like, such as y = (-2)^x. My graphing calculator will not show the graph as anything, but has many real values in a table of values. It is confusing because a negative number to the power of let's say 0.6 (3/5, so odd root) is a real number while a negative number to the power of 0.7 (7/10, so even root) would be an imaginary number. This would mean there are many random points that are both real and imaginary on a graph of this sort. Is it possible to construct a graph of y = (-n)^x because of this interesting coincidence that happens with odd and even roots of the negative numbers?
Each graphing tool will do something a little different.
Doctor Vogler answered:
Hi Alexander,
Thanks for writing to Dr. Math. It depends partly on what you mean by "(-n)^x". You see, generally exponents are either defined algebraically for rational exponents or continuously (through calculus) for positive bases. If you have a negative base and want all exponents (including irrationals) then things get ugly. See also
Base of an Exponential Function
http://mathforum.org/library/drmath/view/55604.html
This is our second question above.
Notice that in the case of all irrational and many rational exponents, the only possible value for y is complex. When graphing, you generally don't graph complex solutions. (Did you plot (i+1, 2i) on your graph of y = x^2? I didn't think so.) So your graph will essentially be dotted lines where the rational values take you. If you plotted those values where x is rational, then you would have a dotted line along y = n^x (since y = n^x when x has an even numerator and odd denominator) and a dotted line along y = -(n^x) (since -y = n^x when x has an odd numerator and odd denominator).
A graphing tool doesn’t know the general picture; it typically chooses regularly spaced values for x and plots points using whatever values of y it finds (if it tries at all). Here is what Desmos shows for \(y=(-2)^x\):
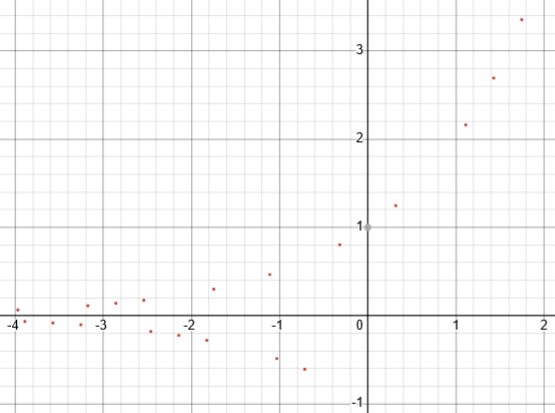
It’s made a valiant effort, showing whatever points it found that work; but those are not all the values of x that represent fractions with an even denominator. For instance, it shows positive values \((-2)^0=1\), and \((-2)^{1.746}=3.354\), and negative values \((-2)^{-1.032}=-0.489\), and \((-2)^{1.032}=-2.044\). All of these lie on the graph of \(y=\pm2^x\):
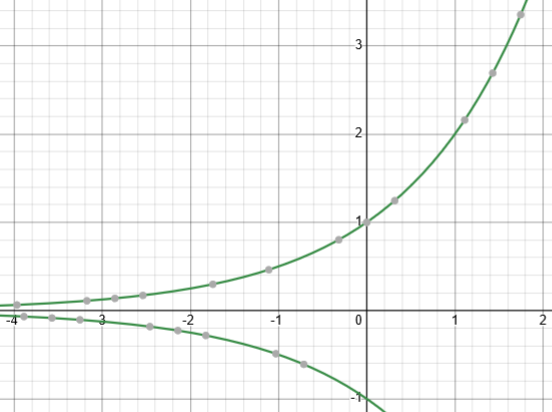
(Zooming in or out changes what points are shown.)
If you want to consider what are the complex values of
y = (-n)^x,
then you have a completely different beast, since there are more than one possible values for y unless x is an integer, and there are infinitely many such values unless x is rational. See also
Complex Powers
http://mathforum.org/library/drmath/view/60383.html
This question is about oddities that arise in complex powers of real numbers (such as \(1^i\)). Similar ideas are found in Complex Powers of Complex Numbers.

Pingback: Logs of Negative or Complex Numbers – The Math Doctors