Powers of Roots and Roots of Powers

Last time, we looked at two recent questions about combining squares and roots, and implications for the properties of exponents. We didn’t have space for some older questions that we referred to. Here, we will go there.

Does a root cancel a power, or not?

First, a question from Cindy in 1997:

Square Root of a Negative Number Squared

I'm reading popular math books in addition to my textbook and am really trying to understand the material.  Here's my question:

I understand that the nth root of x^n = x^(n/n) or x^1.  My textbook gives two problems:  Sqrt(-6)^2 and the 4th root of (-3)^4.  This leads to two different solutions in my mind.  (-6)^2 = 36 so the square root of (-6)^2 = 6. Similarly, the 4th root of (-3)^4 leads to the fourth root of 81, which is 3. 

However, according to the rules, the nth root of x^n = x^(n/n). Therefore, the square root of (-6)^2 should equal (-6)^(2/2) or (-6)^1, which equals -6.  By a similar method, the fourth root of (-3)^4 = (-3)^(4/4) or (-3)^1, which equals -3.

The answers in the back of the book says the correct answers are positive 6 and 3.  Where is the error in my logic?

Although Cindy parenthesized the first expression as a power of a root, \(\sqrt{-6}^2\), she has treated the exponent as inside the radical; so I assume the actual problems were \(\sqrt{(-6)^2}\) and \(\sqrt[4]{(-3)^4}\).

Her first solutions (which give the book’s answers) are $$\sqrt{(-6)^2}=\sqrt{36}=6\\\sqrt[4]{(-3)^4}=\sqrt[4]{81}=3.$$ Here she is just doing what the expressions say.

Her second solutions are $$\sqrt{(-6)^2}=\left(\left(-6\right)^2\right)^{1/2}=\left(-6\right)^{2/2}=\left(-6\right)^1=-6\\\sqrt[4]{(-3)^4}=\left(-3\right)^{4/4}=\left(-3\right)^1=-3.$$ Here she is rewriting as a power of a power and simplifying, which ought to cancel the exponents. Why is the result different?

Doctor Keith answered:

Both you and the book are right in a way.  Your book gives the positive number because, by convention, you always take the positive and real root.  Thus Sqrt((-3)^2) = 3.

As we saw last time, \(\sqrt{x^2}=|x|\) for this reason. The rule of the principal root being the non-negative one only applies to even roots. For odd roots, there is only one real root, which is considered the principal root.

It is important to note that while this is the principal root it is by no means the only one.

This will be the key throughout this post.

I would also like to commend you on noticing that the square root operation yields two roots.  You might be interested to know that if we consider complex numbers (ordered pairs of real numbers, which can be pictured as a plane with the real numbers on the x axis and the imaginary numbers, from sqrt(-1), on the y axis), and you take the nth root (i.e. x^(1/n)), you will actually get n answers! So taking cube roots in the complex plane yields 3 distinct answers, each of which when cubed yields the original number. It provides a beautiful symmetry, and is extremely useful in many applications (I am an engineer and I use this literally all the time).  I find this really neat.

The two square roots of \((-6)^2=36\) are, as we know, \(+6\) and \(-6\):

The four fourth roots of \((-3)^4=81\) are \(+3\), \(+3i\), \(-3\), and \(-3i\):

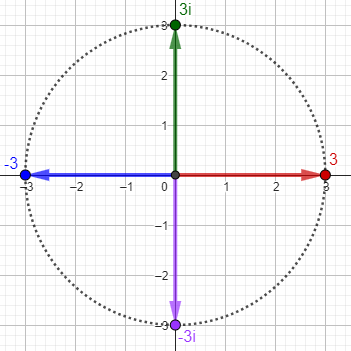
The nth roots of any number are equally spaced around a circle. In both cases, I have shown the principal root in red.

Which root is right?

We got a broader version of the question in 1999:

Fractional Exponents and Complex Roots

We are having a discussion about unique representations of complex roots. 

Does z^(a/b) = (z^a)^(1/b) or (z^1/b)^a, and does z^(1/d) represent the complex number with the smallest positive argument, or is it ambiguous notation for all the d roots?

For example, does [(-4)^2]^(1/4) = 16^(1/4) = the principal fourth root of 16, which is 2, but [(-4)^(1/4)]^2, where if you take the fourth root of -4 with the smallest positive argument and then square it, you get 2i?

The argument of a complex number is its angle. It is common to take the one with the smallest non-negative argument as principal, as in my pictures. But is that what the notation means?

David has shown that, by the power rule of exponents, \(\left(x^m\right)^n=x^{mn}\), we get both \(\left(z^a\right)^{1/b}=z^{a/b}\) and \(\left(z^{1/b}\right)^a=z^{a/b}\). But with negative bases, and therefore complex number results, these can give different results when we try to be consistent in which root we use. On one hand,

$$\sqrt[4]{(-4)^2}=\left(\left(-4\right)^2\right)^{1/4}=\left(16\right)^{1/4}=2$$

Here are all four fourth roots of \((-4)^2=16\); the principal root is in red:

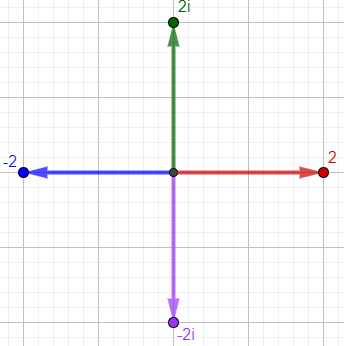
But on the other hand, $$\sqrt[4]{-4}^2=\left(\left(-4\right)^{1/4}\right)^2=\left(1+i\right)^2=2i$$

Here are the four fourth roots of -4, and their (only two!) squares; the principal roots are in red:

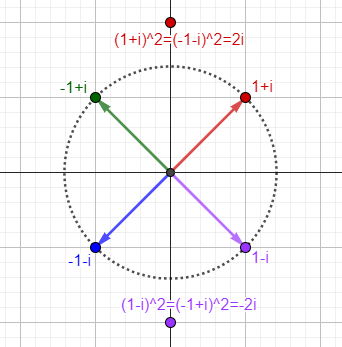
We see that the square of the principal fourth root of -4 is a fourth root of the square of -4, but not the principal root.

It’s ambiguous

Doctor Mitteldorf answered first:

Dear David,

Even simpler, you can take (-2), square it, find the square root, and end up with a different number than you started with.

My advice is to keep your eye on the ball. The conventions are there to serve you, not to confine your thinking, and besides, conventions in this area are murky. You and your students should be aware of this kind of ambiguity, and alerted that when you are trying to find specific solutions to equations, ambiguity may arise so you will need to examine all roots, then think about what makes sense in the context of the present problem.

The example is that \(\sqrt{(-2)^2}=\sqrt{4}=2\), whereas \(\left(\sqrt{-2}\right)^2=\left(i\sqrt{2}\right)^2=-2\). Here, it seems that the square cancels the root, but the (principal) root doesn’t cancel the square!

More accurately … it’s a set

Half an hour later, Doctor Pete joined in, going deeper:

As you can see from your examples, it is generally incorrect to take "principal" values during intermediate steps in evaluation. Doing so is equivalent to losing solutions, and the result is that the normal axioms of associativity, commutativity, and cancellation may be violated. If we are to make any sense of

     z^(a/b)

then it is evident that one must be careful in saying what a "b-th" root of a complex number is. Such a root is not a number, but a set. It is simply not correct to say that

     4^(1/2) = 2.

Rather, when dealing with the complex numbers,

     4^(1/2) = {2, -2}.

Similarly,

     1^(1/3) = {1, e^(2*pi*i/3), e^(-2*pi*i/3)}.

In other words, although we can arbitrarily assign a “principal root”, in this context we have to think of all roots at once, because singling one out will cause inconsistencies.

Because squaring is not injective (one-to-one), as two different numbers, \(2\) and \(-2\), both have the same square, 4, the principal square root, \(\sqrt{4}=2\), is not a true inverse function. With real numbers, we can get away with this, but things get more complicated with complex numbers, and we have to think of the square root, the inverse relation of a two-to-one function, as a “one-to-two function” (mapping), \(\sqrt{4}=\pm2\)

When dealing with complex numbers, one must become accustomed to the idea that functions that are bijective (one-to-one and onto) in the reals are not necessarily so in the complex plane, and hence functions should not be thought of as mappings of a number to a number, but of a set to a set. In the cube root of unity example above, the function

     f(z) = z^(1/3)

is a one-to-three mapping, taking (nearly every) complex number z and mapping it to three distinct elements. Similarly, the inverse function

     f^(-1)(z) = z^3

is a three-to-one mapping, where for a given value of z^3, there are three complex numbers that map to z^3 (one of them being z itself).

So it is at once clear that z^(1/n) is not "ambiguous" in the sense that its value is not specified - what is *meant* by the symbol z^(1/n) is not "the" n-th root of z, but the "n" n-th roots of z. A set of values is no more ambiguous than a single value.

The cube root makes the issues clearer than the square root, because even with a positive real radicand, we get non-real roots. Here are the three cube roots of 8, each of which has the same cube, 8:

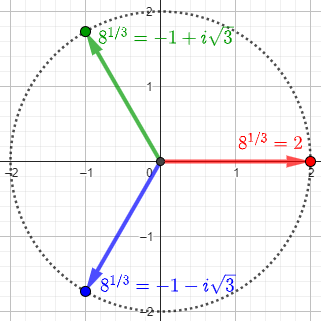
Resolving the question

To demonstrate how this changes your example, consider

     (-4)^(2/4).

Apply the axiom of cancellation to obtain

     (-4)^(1/2) = {2i, -2i}.

This is the correct solution set. On the other hand, one could do it this way:

     (-4)^(1/4) = {1+i, -1+i, -1-i, 1-i}

so

     [(-4)^(1/4)]^2 = {(1+i)^2, (-1+i)^2, (-1-i)^2, (1-i)^2}
                    = {2i, -2i, 2i, -2i}
                    = {2i, -2i}.

Simplifying the 2/4 power to 1/2 yields only the two values, which, as we saw, also result from doing the roots first. But if we do the power first, …

But why isn't

     [(-4)^2]^(1/4) = (16)^(1/4) = {2, 2i, -2, -2i}

valid? This is for the same reason that

     -1 = i^2 = (-1)^(1/2)(-1)^(1/2) = [(-1)(-1)]^(1/2) = 1^(1/2) = 1

is invalid. What's going on is that we're mapping 2-to-1, then 1-to-2, creating extraneous solutions. Since this creates contradictions such as the above, it follows that whenever possible, we first evaluate one-to-many, then many-to-one. So the answer to your original question is that z^(a/b) indicates [z^(1/b)]^a. But this consideration arises only in the case where a and b have a common factor.

So, to avoid extra roots, we need to evaluate \((-4)^{2/4}\) not as \(\left(\left(-4\right)^2\right)^{1/4}\) (taking the four-to-one power first), but as \(\left(\left(-4\right)^{1/4}\right)^2\) (taking the one-to-four root first). This gives the same result as simplifying.

But this isn’t always possible, as we’ll see later.

Fractional powers don’t commute!

A question from 2001 explores what calculators do (which have to give only one answer):

i and (-1) with Multiple Powers

My question is about the order in which i and (-1) should be raised when using multiple powers. The problem that I have run into is that when I change the order of powers I can obtain many different values. This is just one of the many examples I have:

((-1)^(3/2))^(1/3) equals .8660254038-.5i, but when it is simplified to (-1)^(1/2) it of course equals i. Stranger still, when I switch the order of the powers to ((-1)^(1/3))^(3/2), the value equals (-i). 

I have many more examples of this, but they're generally the same. Why is it possible to obtain so many different values? I am quite aware that i's have a nature all their own that negates rules in math that are followed when dealing with real numbers. So what are the rules we MUST follow when dealing with i?

This time, we have two fractional exponents, but the same issue of simplifying vs. commuting the powers: $$\left(\left(-1\right)^{3/2}\right)^{1/3}=\left(-i\right)^{1/3}=\frac{\sqrt{3}}{2}-\frac{1}{2}i$$

$$\left(\left(-1\right)^{1/3}\right)^{3/2}=\left(-1\right)^{3/2}=-i$$

$$\left(-1\right)^{(3/2)(1/3)}=\left(-1\right)^{1/2}=i$$

(My Casio calculator refuses to evaluate \(\left(-1\right)^{3/2}\), so this is a different calculator! Wolfram Alpha gives Kenneth’s values for the first and third, but gives i for the second, so there is a little less trouble.)

Since both exponents are fractions, we can’t follow Doctor Pete’s recommendation and do the fractional power first! So the answer will have to be, there is no one correct answer. What did the calculator do?

I answered:

Hi, Kenneth.

It sounds as if you are finding powers on a calculator without stopping to think about what they mean. Let's think about that a moment.

We're working with complex numbers here. Recall that x^(1/2), the square root, has _two_ values, not just one; in real numbers we can choose one as the primary root, but we can't even do that in complex numbers. Further, there are _three_ cube roots, _four_ fourth roots, and so on. So it really shouldn't surprise you at all that you can get several different values for the same expression; they are all correct! What should be surprising is that the calculator would tell you that one of them is "the" answer. That's the real cause of the difficulty; whatever rule they use to decide which answer to give produces different results when you do it in a different order. It would be better if it told you somehow that this is only one of a certain number of values.

This is one of the shortcomings of calculators: They can’t explain themselves, so they just quietly choose something to do, even when no one answer can be correct.

So let's try doing the calculation as if we were the calculator, doing just what we're told. The expression

    [(-1)^(3/2)]^(1/3) 

tells the calculator to raise -1 to the 3/2 power, which it probably does by taking "the" square root, i, and cubing it, to get -i. (Of course, this is actually the other square root of -1.) It would be equally valid to take -i as the square root and cube it to get i; but let's forget that for now. 

Now the calculator will take "the" cube root of this, which might be done either by thinking of it as having angle 270 degrees and dividing by 3 to get 90 degrees (giving the cube root as i); or it might think of the angle as -90 degrees and take the cube root with angle -30 degrees. The latter agrees with the answer you give.

So the calculator takes the red root as principal, though there are three other choices when we take \(\left(-1\right)^{3/2}=-i\):

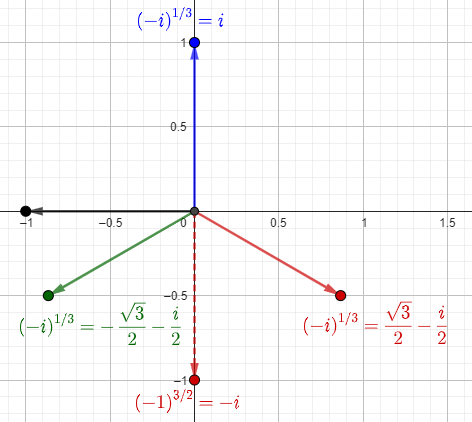
There are 3 other answers if we took the other root, \(\left(-1\right)^{3/2}=i\):

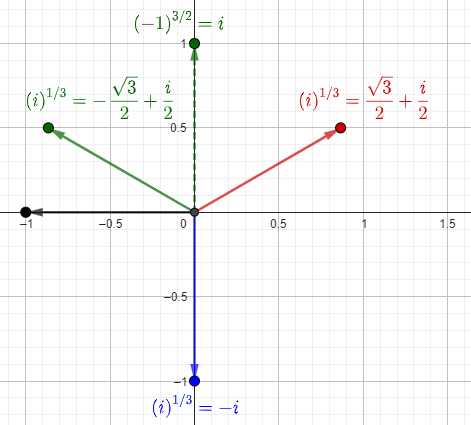
Since there are two square roots and three cube roots, there will be six possible values for this expression. You've found ways to get three of them. See if you can do the same thing I just did to explain

    [(-1)^(1/3)]^(3/2)

I'd get i, myself; but we don't know for sure what rules the calculator is using. You might want to read the manual to see if they tell you, or keep it a secret.

As I said above, Wolfram Alpha also gets i. I can’t see what Kenneth’s calculator might have done.

Does (a^b)^c = a^(b*c) always?

We’ll close with a long question from 2009, which we explicitly referred to last time:

Does (a^m)^n Always Equal a^(mn)?

I'm in training to be a math teacher--and I want to know the laws of exponents with all their gory exceptions and complications. 

One law for exponents states: (a^m)^n = a^(mn).  However, is this always true?  For instance, is it true that (a^2)^(1/2) = a^1 = a?

It doesn't seem that it can be for ((-3)^2))^(1/2) since it can be evaluated one of two ways:

ONE: evaluating the "inside" first yields 9^(1/2)= 3 OR
TWO: evaluating the "outside" first (by multiplying the exponents and applying the law) yields (-3)^1= -3.

So which of these answers is correct--and why?

My calculator (a TI-89) indicates the first one (positive 3), which would be consistent with evaluating from left to right, as the order of operations requires when operations are on the same level.

In addition, I've always read that SQRT(X^2) is the ABS(X), which makes sense and is consistent with my first answer.  If this is right, this would mean the above law is NOT always true. 

However, I never see this exception mentioned in the laws of exponents that are presented to students.  Generally, these laws are claimed to hold for all real number bases and exponents, with the exception of 0^0.

In addition, I also note that if you evaluate ((-3)^(1/2))^2 you get the same answer either way you proceed:

ONE: evaluating the inside first yields (i*SQRT(3))^2= -3 and
TWO: evaluating the outside first yields, once again, (-3)^1= -3.

My TI-89 gives me the same answer as well (negative)

Yet were the above exponent law to apply, I could apply the commutative law and rearrange the exponents from 1/2 * 2 to 2 * 1/2 and thus regenerate the above problem.

It seems to me that the particular "law" of exponents in question is really only valid for a > 0.  Am I correct?  Is there some gory list of rules of how to deal with these situations?

Any help would be much appreciated.

We’ve already seen answers to all these questions, which are nicely summarized here; but another opinion will be useful.

Doctor Vogler answered:

Hi Adam,

Thanks for writing to Dr Math.  That's a very good question.  The usual convention is that when x is a positive number, then sqrt(x) is also taken to be the positive square root.  Of course, really there are two square roots, and ignoring that fact can cause problems.

When taking roots of complex numbers, we have no such convention (e.g. why should the square root of -2i be 1-i instead of i-1?), and we simply deal with the fact that every nonzero complex number has exactly n (different) complex n'th roots.  For example, the number 9 has TWO square roots, namely +3 and -3.

According to Wikipedia, there is a definition of the principal square root, so that \(\sqrt{-2}=1-i\), and this could be generalized to the principal nth root; but this doesn’t prevent any of the difficulties we’ve seen.

The "rule"

  (a^b)^c = a^(b*c),

which works so nicely for integer exponents and even for non-integer exponents when the base is positive, becomes problematic with negative or complex bases and non-integer exponents.  You see, when n is an integer, then x^n has only one value, but when n is a rational number with (least positive) denominator d, then x^n has d different complex values, and when n is irrational, then x^n has infinitely many different complex values.

The rule (a^b)^c = a^(b*c) should be interpreted as:  Every value of a^(b*c) is one of the values of (a^b)^c.  (It doesn't even work in the other direction, since sometimes some of the values of (a^b)^c aren't any of the values of a^(b*c).  For example, -1 is one of the square roots of 1^2.)

I don’t know whether it could be proved that there is no other interpretation of this rule, or of the principal value of a rational power, that will make it always true, but that seems very likely. This interpretation seems to be the best we can do.

Adam thanked us:

Thanks so much for your detailed and prompt response. It was exactly what I was looking for. 

Wow, x^pi has infinitely many values--amazing.

Indeed!