Having answered many questions recently about logarithms, I realized we haven’t yet covered the basics of that topic. Here we’ll introduce the concept by way of its history, and subsequently we’ll explore how they work.
What does that button do?
We’ll start with this 1998 question:
'Log' Button In math we have been using the 'log' button on our calculators to solve problems that involve compound interest, etc., and our teacher says we'll learn what the 'log' button does next year. But we want to know now! The teacher says it has something to do with the opposite of exponents, but I still have no clue.
I sometimes struggle with the order in which to explain things, because when you need to use a new concept, sometimes the students aren’t ready for the concept on which it is based, so they can’t fully understand it (and perhaps don’t really need to). So we may have to tell a student, just use it for now. But I’m with the student: Some sort of explanation would be nice.
Doctor Sam answered Brad in that spirit:
Well, logarithms can be a big topic and if you are interested you might try reading about them in another math book. But for a quick introduction, here goes: First, the word logarithm is really a synonym for the word exponent or power.
I tell students, “the logarithm is the exponent”; what I mean by that is that when we see that, say, \(10^4=10,000\), we can say that 4 (the exponent) is the logarithm of 10,000. And that’s what the teacher means by “the opposite of exponents”: When we find a logarithm, we are finding what exponent is needed to get that number. We’re working backward.
Second, there are lots of different kinds of logarithms depending upon the base you are using.
The LOG key on your calculator is probably "base 10 logarithm". Try this: make a table of values of different powers of 10, like this:
power x: -2 -1 0 1 2 3 ...
10^x: 0.01 0.1 1 10 100 1000 ...
Ordinarily we read these as "10 to the power 2 equals 100" or "10 to the power 3 equals 1000."
This is fine when you need to calculate a power of ten, but what if you know the answer and need to find the exponent? To solve 10^x = 10000, for example, you have to think "ten to what power is ten thousand?" That's not too hard. But what if the problem is 10^x = 25?
So far we just have a name (“logarithm”, or “log” for short) for what we want to do. The table gives us a method, but only in the easiest cases.
LOGARITHMS were invented (back in the sixteenth century I think) to answer these kinds of questions.
LOG(25) means "the power of 10 that produces 25" and
LOG(1000) = 3 because "the power of 10 that produces 1000 is 3."
You can make a little table of logarithms just by switching the two rows of my table above:
10^x: 0.01 0.1 1 10 100 1000 ...
power x: -2 -1 0 1 2 3 ...
only now the second row is called the logarithm. So here it is one more time:
n: 0.01 0.1 1 10 100 1000 ...
LOG(n): -2 -1 0 1 2 3 ...
The trouble is, when we want to fill in numbers in between, none of the arithmetic you’ve learned can do it; there is no simple formula for the log. (That’s why we need a name, and a calculator button for it!)
What we’re doing here is finding the inverse of the exponential function: $$\text{If }y = 10^x\text{, then }x=\log(y)$$
Back in the sixteen hundreds (in fact even back in the dark ages when I went to school in the 1960's) we didn't have pocket calculators with LOG keys. Companies published books of tables, page after page of the powers of 10 that would give you almost any number you wanted. It's a lot easier to press a key!
Here’s an example of such a table, from the book I used in college (CRC Standard Mathematical Tables):
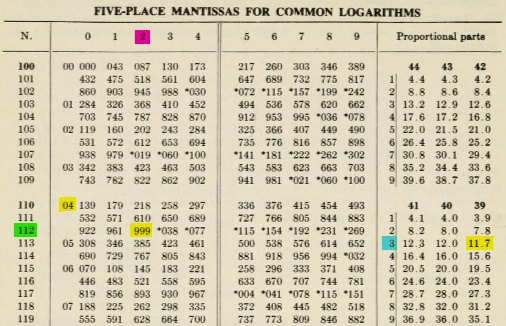
The table gives the “mantissa”, or decimal part, of logarithms, which is the log of a number from 1 to 10.
For example, to find the logarithm of 1.1223 I find 112 in the left column and 2 on the top, leading me to 04 999; then I see that the next number to the right, 04 038, is an increase of 39, and the little table at the right tells me that 3/10 of 39 is 11.7. So I add \(04999+11.7=05010.7\), and move the decimal point to the start, \(0.050107\). A calculator shows it to be \(0.0501089\dots\). The table claims to be accurate to five places, so we’d round our answer to \(0.05011\), which agrees.
Yes, calculators are easier …
By the way, when we look up numbers in the table in reverse, finding the number whose log is a given value, they called this the “anti-log“, because they thought of the log as the main thing, what the table was made for — but in a modern view, it’s the exponential that’s primary and the log is its inverse. So what was called the anti-log is, in fact, just the exponential function.
I do want to mention that the little table I used gives powers of 10, and so these are called base ten logarithms (or COMMON LOGARITHMS). But almost any number can be used as the base. If you are interested in solving problems with powers of 2 (175 = 2^x) it would be helpful to have a base two logarithm key on your calculator. You probably don't have one, but computer scientists who use powers of two a lot do.
We’ll see more about these other bases soon.
Common logarithms as a calculation tool
Here’s a look at the history of logarithms, from 1996:
Logarithms: History and Use I have been asked to explain logarithms from a non-numerical sense to non-math-oriented people. It doesn't seem to be enough for me to show the equation and how it works, they want to know why. Any thoughts? Also, do you have short anecdotal history for the development of the concept of logarithm? Finally, why is it called a "logarithm"? logos = reason, arithmos = number.
Doctor Anthony answered the history aspect of Linda’s question, starting with two different purposes for logs:
It is a very great economy of effort if we can reduce multiplication to the addition of two numbers. The possibility of adding numbers that can be looked up in tables compiled "forever," as Napier remarked, instead of carrying out a lengthy process of multiplication, was suggested in two ways that were quite independent. The first arose in connection with the preparation of trig. tables for use in navigation. The second was closely connected with the laborious calculation involved in reckoning compound interest on investments.
Tables of trigonometric functions already existed, and it was found that they could be used as a calculating tool:
In 1593 two Danish mathematicians suggested the use of trig. tables for shortening calculations. They used the formula: sin(A)*cos(B) = (1/2)sin(A+B) + (1/2)sin(A-B) Thus to multiply 0.17365*0.99027, you look up in tables and find 0.17365 = sin(10), 0.99027 = cos(8) and the above formula gives sin(10)*cos(8) = (1/2)(sin(18) + sin(2)) From tables sin(18) = 0.30902 sin(2) = 0.03490 sin(18) + sin(2) = 0.34392 and (1/2)(sin(18)+sin(2)) = 0.17196 Giving 0.17365*0.99027 = 0.17196
This formula is called the product-to-sum identity. Four table lookups and an addition took less work (and was less error-prone) than doing the multiplication by hand.
This device probably suggested to Napier, who is usually called the inventor of logarithms, a simple method for multiplying by a process of addition. Napier had been working on his invention of logarithms for twenty years before he published his results, and this would place the origin of his ideas at about 1594. He had been thinking of the sequences which had been published now and then of successive powers of a given number. In such sequences it was obvious that sums and differences of indices of the powers corresponded to products and quotients of the powers themselves; but a sequence of integral powers of a base, such as 2, could not be used for computations because the large gaps between successive terms made interpolation too inaccurate. So to keep the terms of a geometric progression of INTEGRAL powers of a given number close together it was necessary to take as the given number something quite close to 1. Napier therefore chose to use 1 - 10^(-7) or 0.9999999 as his given number. To achieve a balance and to avoid decimals, Napier multiplied each power by 10^7. That is, if N = 10^7[1 - 1/10^7]^L, then L is Napier's logarithm of the number N. Thus his logarithm of 10^7 is 0. At first he called his power indices "artificial numbers", but later he made up the compound of the two Greek words Logos (ratio) and arithmos (number).
For more details on the word, see here; and here (including how “reason” and “ratio” are related). A given difference in logarithms corresponds to a given ratio of numbers.
Napier did not think of a base for his system, but nevertheless his tables were compiled through repeated multiplications, equivalent to powers of 0.9999999 Obviously the number decreases as the index or logarithm increases. This is to be expected because he was essentially using a base which is less than 1. A more striking difference between his logarithms and ours lies in the fact that his logarithm of a product or quotient was not equal to the sum or difference of the logarithms. If L1 = log(N1) and L2 = log(N2), then N1 = 10^7(1-1/10^7)^L1 and N2 = 10^7(1-1/10^7)^L2, so that N1*N2/10^7 = 10^7(1-1/10^7)^(L1+L2), so that the sum of Napier's logarithms will be the logarithm not of N1*N2 but of N1*N2/10^7. Similar modifications hold, of course, for logarithms of quotients, powers and roots. These differences are not too significant, for they merely involve shifting a decimal point.
So the first “logarithms” weren’t quite what we think of now.
Napier's work was published in 1614 and was taken up enthusiastically by Henry Briggs, a professor of Geometry at Oxford. He visited Napier and discussed improvements and modifications to Napier's method of logarithms. Briggs proposed that powers of 10 should be used with log(1) = 0 and log(10) = 1. Napier was nearing the end of his life, and the task of making up the first table of common logarithms fell to Briggs. Instead of taking powers of a number close to 1, as had Napier, Briggs began with log(10) = 1 and then found other logarithms by taking successive roots. By finding sqrt(10) = 3.162277 for example, Briggs had log(3.162277) = 0.500000, and from 10^(3/4) = sqrt(31.62277) = 5.623413 he had log(5.623413) = 0.7500000. Continuing in this manner, he computed other common logarithms. Briggs published his tables of logarithms of numbers from 1 to 1000, each carried out to 14 places of decimals, in 1617. Briggs also introduced the words "mantissa" for the positive fractional part and "characteristic" for the integral part (positive or negative).
These last two terms were important in using tables, but not so much today.
The first tables of logarithms contained inaccuracies which were noticed and corrected from time to time. The labor expended in constructing them was enormous, and it stimulated the search for better methods of calculating them. This gave a new impetus to the study of infinite series, for example sqrt(2) = (1 - (1/2))^(-1/2) which gives rise to an infinite, convergent series when expanded according to the binomial theorem. This work culminated in the extremely important exponential series, where e = Limit {1 + 1/n}^n as n -> infinity. It is easy to show that
e^x = Limit {1 + 1/n}^(nx)
generates the series shown below:
e^x = 1 + x + x^2/2! + x^3/3! + x^4/4! + ... to infinity, and
e = 1 + 1 + 1/2! + 1/3! + 1/4! + .... = 2.718281828...
e is now used as the base of logarithms in almost all advanced work.
Modern calculators use something related to this when you push the button. And this number e leads us to the natural logarithm:
Natural logarithms and compound interest
Doctor Anthony mentioned a second purpose for logarithms, related to compound interest. That comes up in this 1998 question:
History and Applications of the Natural Logarithm We have been using e in continuous growth problems, where we are examining the growth potential of natural disease populations. I'm so surprised at how often this number comes up in other applications, though. Where did e come from? Who first derived it? Why is it so common in the field of biology?
The question is about the number \(e\approx2.71828\dots\), which is the base of the natural logarithm, called \(\log_e(x)\) or \(\ln(x)\) (and often just written as \(\log(x)\) at higher levels, where it is the default).
Doctor Rob answered:
John Napier, the inventor of logarithms, is credited with discovering this constant. Leonhard Euler is credited with popularizing the use of the letter e for this number. There are two reasons for its frequent appearance in mathematical contexts. The first is that it is the limit, as n grows without bound, of (1 + 1/n)^n. This particular definition lends itself to problems involving continuous compounding of interest. Think of adding 1/n of the current total to that current total n times.
This formula would represent compound interest at a rate of 100%, compounded n times a year. As we compound more often, so that our interest earns interest, we earn more; so that with continuous compounding, rather than doubling in a year, the investment would be multiplied by 2.718. In fact, with daily compounding, the amount after a year would be $$\left(1+\frac{1}{365}\right)^{365}=2.714567\dots$$ Hourly compounding would yield $$\left(1+\frac{1}{365\cdot24}\right)^{365\cdot24}=2.718126\dots$$
The result is that when interest on principal P is compounded continuously at an annual rate of r, the amount after t years is $$A=Pe^{rt}$$ The natural logarithm, the log with base e, is the inverse function, so to find the time at which a certain amount is obtained, we take the logarithm of the ratio \(\frac{A}{P}\): $$t=\frac{1}{r}\log_e\left(\frac{A}{P}\right)$$
The second is that e is the only constant such that the slope of the graph of y = e^x at 0 is 1; or, in other words, the function e^x is the solution of the differential equation dy/dx = y, with initial conditions y = 1 when x = 0. Similarly, the solution of dy/dx = a*y, with initial conditions y = 1 when x = 0, is e^(a*x).
Here are the graphs of exponential functions with several different bases (2, e, 10), showing that the slope of \(y=e^x\) at \(x=0\) is 1:
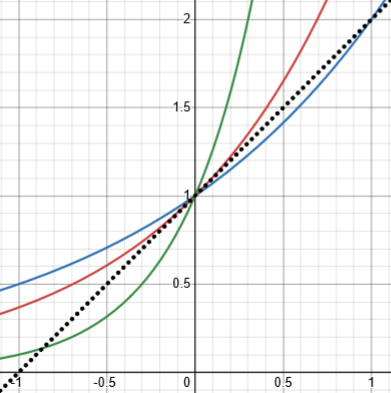
This is the reason that e, and natural logs, are ubiquitous in calculus and related higher mathematics.
The logarithm is the inverse function, obtained by swapping the roles of x and y:
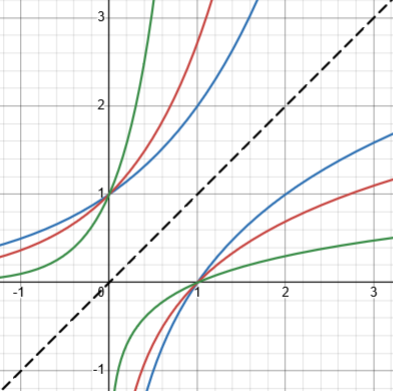
This is the biological connection. You are talking about the instantaneous rate of growth of something being proportional to the amount of the something. That something can be a population of bacteria in a culture, or a population of cockroaches in a garbage dump. Here, "k" represents the fraction of them reproducing at any given time x. If "k" is negative, it could represent the fraction of organisms dying at any given time.
Unrestricted growth follows an exponential function, derived from that differential equation, namely $$N=N_0e^{kx}$$
This is the model for radioactive decay of radium, uranium, and so on. This is also the approximate model for inflation -- exponential growth.
Radioactive decay is exponential growth is the same, with a negative rate: $$N=N_0e^{-kx}$$
The way to calculate e is by using as many terms as necessary for the accuracy you need in the following infinite series:
e = 1 + 1 + 1/2 + 1/(2*3) + 1/(2*3*4) + 1/(2*3*4*5) + 1/(2*3*4*5*6)
+ ...
The terms shown above are already enough to obtain a value for e that is roughly 2.718.
It’s worth pointing out that we can actually use any base we want to describe these growth and decay problems; we’ll see that in another post. But the natural exponential, and the natural logarithm, are what arise directly from the differential equation, and directly display the growth rate.
Relationship between common and natural logs
We’ll close with a 2005 question to tie things together:
Common Logarithms and Natural Logarithms I am currently studying logarithms and I saw that logarithms can take the form of ln or log. What is the difference between the two? I think it's very confusing because I looked it up in my math book and they state log e x = ln x. Then they state log 10 x = log x. I am confused about how e and 10 work with ln and log. I think that if I see a problem such as y = ln(x-1) and the book asks to find the inverse, I have to change it to log, but I don't know how to do that. I simply don't understand ln and log's relationship.
Doctor Tom answered, starting with the common logarithm:
Hi Katie, You're confused because it really is confusing! When logarithms are first introduced, it is much easier for students to think about logarithms in base 10. In base 10, log(.01) = -2 log(.1) = -1 log(1) = 0 log(10) = 1 log(100) = 2 log(1000) = 3 an so on--it just sort of counts the zeros, or, more accurately, the log is the power of 10 that creates the number you are taking the log of. Since 100 is 10^2, the log of 100 is 2.
Using common logarithms, we only need a table for values between 1 and 10, because $$\log(a\cdot10^n)=\log(a)+\log(10^n)=\log(a)+n,$$ so we can separately find the “characteristic” (the whole number part) and the “mantissa” (the fractional part) of the logarithm. For example, $$\log(112.23)=\log(1.1223\cdot10^2)=\log(1.1223)+\log(10^2)=\log(1.1223)+2\approx0.05011+2=2.05011$$
Engineers also tend to use log base 10 for most calculations for the same reason. You can just look at the size and know the magnitude of the number. if the log (base 10) is 5.46, without even thinking, you know the number is "between" 10^5 and 10^6, so it's between 100,000 and 1,000,000. So in introductory texts and in engineering books, when you see "log", it usually means "log base 10". If they DO want to talk about other bases, they either put a little subscript after the "log", like "log_e". (I can't draw a subscript, so I'm using the "_" to mean that the next character should be smaller and written as a subscript).
So \(\log\) is just a nickname for the common log, \(\log_{10}\); and \(\log_{e}\) is the natural log, nicknamed \(\ln\).
Since log base e is often important for engineers, particularly electrical engineers, they often use "ln" instead of "log_e" since it's quicker to write, and it's a mnemonic for "logarithm, natural", or "natural logarithm". Now for mathematicians, the "natural log" really IS much more natural, so since that's the ONLY type of logarithm they use, they often just write "log" instead of "ln". I know this seems really confusing, but if you know what you're doing, you can almost always tell that it's a natural log just by looking at the equation. Of course if there is a chance of confusion, everybody always writes them like "log_10" or "log_e" to make it obvious what's going on.
So “log” means the default in whatever field you are in. (This can cause confusion if you look around online, because you may stumble into a world other than that of your class, in which, say, “log” is used where your teacher would use “ln”. Be careful!
Since you are just starting to learn about logarithms, you will always see "log" as meaning "log_10". Computer scientists often have a very good use for "log base 2", or "log_2", and it comes up so often there that they often write "lg" instead of "log_2". I've never seen them shorten "lg" or "log_2" to just "log" like the mathematicians, however, so you're never in any danger there.
In fact, it is not uncommon in computer science today for “log” to mean base 2. Wikipedia says,
Many disciplines write log x as an abbreviation for logbx when the intended base can be inferred based on the context or discipline (or when the base is indeterminate or immaterial). In computer science, log usually refers to log2, and in mathematics log usually refers to loge . In other contexts, log often means log10.
When you solve a problem, check how the symbol is used in your source.
We’ll see more about logarithms next time.

Pingback: Why Do Logarithms Work That Way? – The Math Doctors
Pingback: Why Can’t a Logarithm Have a Negative Base? – The Math Doctors