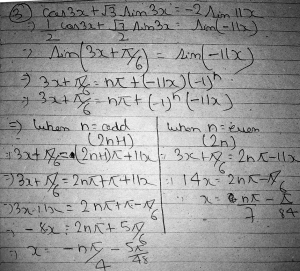(A new question of the week)
In many areas of math, an answer can come in several forms, which can make it hard to know if you are right when you compare your answer to the answer in the back of the book. Even worse is when the problem is multiple-choice, and your answer has a different form than the choices given. This can happen very easily in trigonometry. What do you do?
This happened to a student recently, and he wrote to us to help unravel it. Here is his question:
Here is the problem I am working on:
The general solution of the equation \(\tan^2\alpha + 2\sqrt{3} \tan\alpha = 1\) is given by …
(A) \(\alpha = \frac{n\pi}{2} (n\in I)\)
(B) \(\alpha = (2n+1)\frac{\pi}{2} (n\in I)\)
(C) \(\alpha = (6n+1)\frac{\pi}{12} (n\in I)\)
(D) \(\alpha = \frac{n\pi}{12} (n\in I)\)I have tried solving it this way:
Firstly I applied the Quadratic Formula to get,
\(\tan(\alpha) = -(2+\sqrt{3}) \text{ or } (-\sqrt{3}+2)\)
Now we have two cases,
CASE 1: When \(\tan(\alpha) =\tan(\pi/12) = 2-\sqrt{3}\).
So General Formula here will be, \(\alpha =n\pi + \pi/12\).
Now, CASE 2: When \(\tan(\alpha) =\tan(-5\pi/12) = -(2+\sqrt{3})\).
So General Formula here will be \(\alpha = n\pi – 5\pi/12\).
I do not know what should I do next to get the answer? Please tell me how to proceed further.
The answer given in the key is the option (C).
I will be thankful for any help!
He’s done good work, solving the quadratic equation to find two possible values for \(\tan(\alpha)\), and then finding all values of \(\alpha\) for each case. The difficulty is that the choices are given in ways that blend all solutions into a single formula using an integer parameter, while Navneet has two separate formulas, neither of which looks quite like any of the choices, though there is a clear similarity. How do you blend them? Or is there another way to decide?
After checking his work, I answered:
You have the solution; now you just have to put it in the desired form.
For this sort of multiple-choice problem, all you need to do is to compare your solution to each choice. Your solution, written as a pair of lists, is (taking n=0, 1, 2, …)
α = π/12, 13π/12, 25π/12, … or -5π/12, 7π/12, 19π/12, …
That is, putting these together,
α = …, -5π/12, π/12, 7π/12, 13π/12, 19π/12, 25π/12, …
There are two directions to go from here. Either do what I just did with each of the choices, and find which one matches; or observe that successive solutions actually differ by 6π/12 = π/2, so that the solution in simpler form is a single arithmetic sequence,
α = π/12 + n π/2.
Now you can see that two of the choices have π/12 factored out, so you can do that to your solution:
α = π/12 (1 + 6n)
and we have the answer.
Of course, if this were not multiple-choice, your original answer would have been acceptable, though you might want to do the same work I did here just to find a somewhat neater form.
The fact that the question was multiple-choice provided a hint at the desired form (a single combined formula), which would not have been present in an open-ended question (where we would have faced the similar issue of determining whether the answer in the book agreed with ours). This is similar to the difference between a problem that asks us to simplify an expression (which might have many “simpler” forms, all equally valid in the absence of specific instructions), versus one that asks us to prove a trig identity (where we are in essence told what the answer is, and just have to get there). Seeing the form of the choices, we had some ideas for directions to take our work.
(We could instead have used the basic strategy for multiple-choice problems, not actually solving at all but just checking each proposed solution. A and D both make 0 a solution; clearly that doesn’t work in the equation. B makes π/2 a solution, which is wrong (the tangent is undefined). So only C is left. But I can’t stand doing that; it works against the whole idea of learning, testing an entirely different skill than what is supposed to be learned. A better-designed question might at least make this method harder, and force you to do a little actual math.)
Four days later, the same student asked a related question that was not in a multiple-choice context and did not involve merging two sets of solutions, but was actually more interesting:
I am again facing a problem in solving a question of this type.
See question number 3 in the attachments:
Problem 3:
Solve the equality: \(2 \sin 11x + \cos 3x + \sqrt{3}\sin 3x = 0\)
Answer:
\(\displaystyle x = \frac{n\pi}{7} – \frac{\pi}{84} \text{ or } x = \frac{n\pi}{4} + \frac{7\pi}{48},\ n \in I\)
This is my solution:
One of the solutions is matching with the solution given in my textbook but the other solution is not matching.
Why isn’t my solution matching with the solution given in my textbook?
I will be thankful for help!
This is an open-ended problem, where our difficulty is not in choosing an answer, but in deciding whether we are right. Navneet’s first answer should agree with the book’s second, but looks quite different. In fact, if we try choosing a value for n and seeing whether the answers agree, it looks at first as if it must be wrong.
I had to think a bit before I answered:
At first I thought this might be an actual arithmetic error, but then I saw that it is just a more complicated version of the previous kind of issue.
First, I was impressed by the way you wrote a single expression initially for all angles whose sine is the same as for -11x; but then I saw that you turned that into what I would have written first, giving two separate cases (for n odd and even). I presume the first form is one you were taught, that I have not seen.
All your work is excellent, and very clearly written.
But your answer seems different from theirs in the odd case. Why? To see what they probably did, try replacing 2n+1 with 2n-1 in your work, which is equally valid, and see what you get!
It turns out that they, again, just made a different choice than you, which led to their n having a different meaning in that case. Looking at the problematic half of the answer, they have n pi/4 + 7 pi/48 [= (12n + 7)pi/48], while you have -n pi/4 – 5 pi/48 [= (-12n -5)pi/48]. Here are the values for some values of n:
n theirs yours
-2 -17pi/48 19pi/48
-1 -5pi/48 7pi/48
0 7pi/48 -5pi/48
1 19pi/48 -17pi/48
2 31pi/48 -29pi/48These are, in fact, the same solutions, but in reverse order and starting at different places! As before, doing this at least can reassure you that your solution is correct, even though it has a different form.
When you do what I suggested above, you should see why.
Interestingly, I recently wrote a blog post in part about a similar issue that occurs in calculus, where two solutions can look entirely different, and the difference turns out to be absorbed in an arbitrary constant. Here, the difference is “absorbed” by an index that can start in different places or move in different directions.
Let’s “do what I suggested above” to see what I meant. Here is Navneet’s work, using \(2n+1\):
\(3x+\pi/6 = (2n+1)\pi + 11x\)
\(3x+\pi/6 = 2n\pi +\pi + 11x\)
\(3x – 11x = 2n\pi + \pi – \pi/6\)
\(-8x = 2n\pi + 5\pi/6\)
\(\displaystyle x = -\frac{n\pi}{4} – \frac{5\pi}{48}\)
Here is my work, using \(2n-1\):
\(3x+\pi/6 = (2n-1)\pi + 11x\)
\(3x+\pi/6 = 2n\pi -\pi + 11x\)
\(3x – 11x = 2n\pi – \pi – \pi/6\)
\(-8x = 2n\pi – 7\pi/6\)
\(\displaystyle x = -\frac{n\pi}{4} + \frac{7\pi}{48}\)
This is their solution!
As we can see, when the book’s answer looks different from ours, we can (a) “spot check” some values to see that it doesn’t really disagree; (b) write both answers in a common form, such as a list of values, to see that they actually agree; or (c) take the form of their answer as an addendum to the question, suggesting the form we should try, and proceed in that direction. With experience, we can learn how an answer can be disguised (here, by reversing the direction of the index n), and not be too surprised.
Or, we can ask the Math Doctors!