Sines Without Right Triangles

(A new question of the week)

A recent question dealt with an apparent conflict between the right-triangle definition of sines and cosines, and the unit-circle definition, pertaining to multiples of 90° (angles on the axes). This provides an opportunity to look closely at the relationship between those two definitions.

Two definitions

Recall that the right-triangle definition of the sine, for acute angles, is “opposite over hypotenuse”:

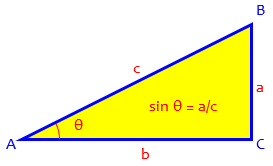
The unit-circle definition of the sine (which applies to any angle) is simply the y-coordinate of a point on the unit circle:

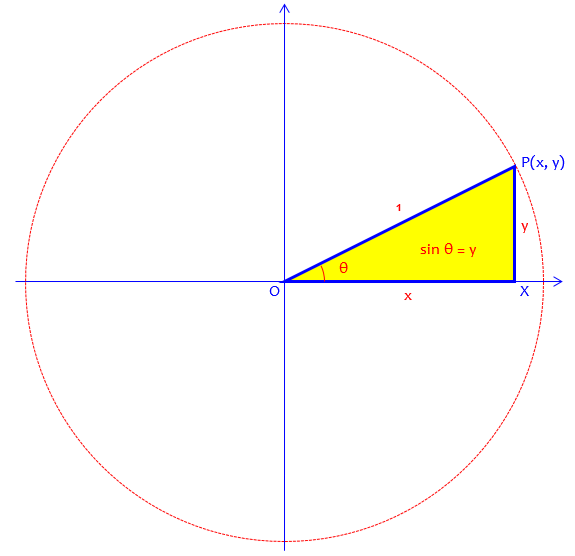
Clearly they agree for angles in the first quadrant.

Here is another right triangle, this time in the second quadrant:

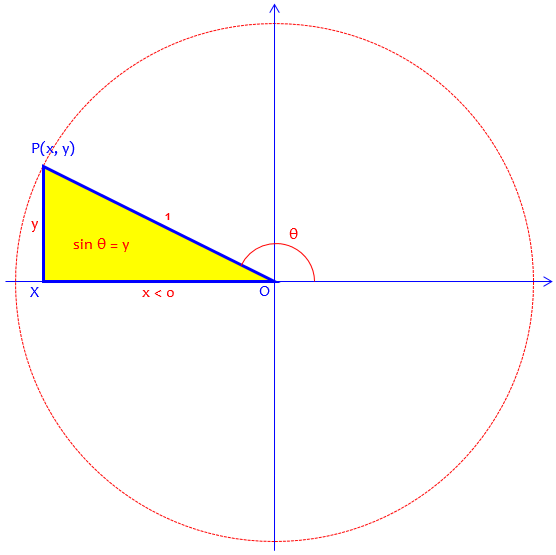
Here, the right-triangle definition is closely related to the reference angle, which in this case is \(180°-\theta\). But we can’t draw a right triangle with an obtuse angle, so that definition doesn’t apply here.

What about points on the axes?

Here is the question, from mid-March:

On the unit circle, how can we be sure that the (x, y) values that lie on the x and y axes correspond to the cosine and sine values at that angle?

What I mean is that on the unit circle, there are the ordered pairs (1, 0), (0, 1), (-1, 0), and (0, -1) that, just like any other ordered pair, correspond to the cosine and sine values of the angle needed to get to that point with x=cosine and y=sine. However, in order to prove that the x and y values equal the cosine and sine values, it is necessary to construct a right triangle that uses the x and y values as the legs of the triangle and the radius of 1 as the hypotenuse. Problem is, this can’t be done using the points I mentioned as they lie on the x- or the y-axis, so how can we be sure that the rule we proved for all the other points works for those specific points?

At first, I thought it followed from the graph of the trig functions, but the graph is a mapping of the points from the unit circle. The values at those points still need to be proven to have those points on the graph be filled in, so that can’t be it.

For example, the point (0, 1), corresponding to a 90° angle, looks like this, where the “triangle” isn’t a triangle:

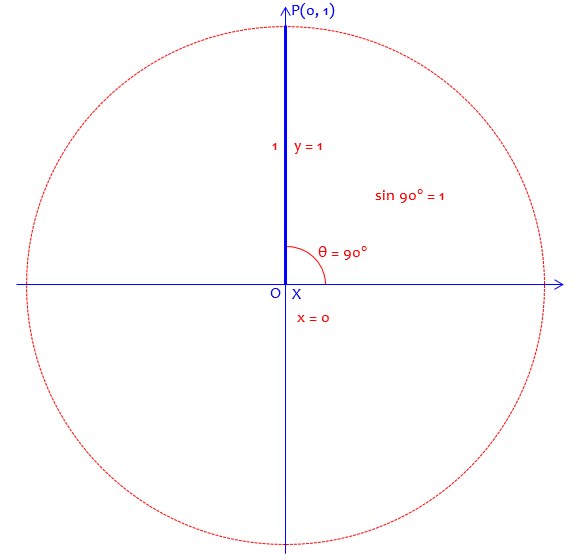
Extending the definition

Doctor Rick answered:

Hi, Mario.

Underlying your questions, I believe, is the assumption that the trigonometric functions are defined via right triangles and all of trigonometry must be based on those definitions. This is not actually true; if it were true, the trig functions would only be defined for angles 0 < θ < π/2. Something must be added to the definitions, right? Those definitions are not sufficient in themselves.

We don’t know just how the unit circle was presented in Mario’s class; I have seen several very different approaches, and in fact there are textbooks whose titles include something like “A Right-Triangle Approach to Trigonometry” or “A Unit-Circle Approach”, indicating what definitions they start with; and the introductions may suggest alternative paths through the chapters for teachers who want to start a different way.

Presumably, the right-triangle definition was presented as the initial definition, and the unit-circle definitions were derived from them, or at least justified on that basis. Mario is likely misunderstanding what the book was saying, because you can’t actually prove a fact for non-acute angles from a definition that doesn’t apply to them. Doctor Rick suggests a better way to see the relationship:

A better way to think about the unit-circle definitions is as an extension of the definition of trig functions to any angle. It’s a little like the way the basic concept of exponents, which is first applied to positive-integer exponents (x³ = x·x·x, for instance), is extended to give meaning to negative-integer powers, then to rational powers, and to real-number powers (and even on to complex powers).

This is common in mathematics, sort of a bootstrapping approach; I discussed the idea in the post What is Multiplication … Really? A concept, such as addition, multiplication, or exponent, is first conceived in the context of whole numbers, and then applied to new forms of number as they are invented. Here, the trig functions are first thought of in terms of acute angles, and then extended.

In other words, once the unit-circle definition is established, it replaces the right-triangle definition as the basis on which things are proved. We then work in the opposite direction from what you suggested: we show that, in the case of 0 < θ < π/2, the right-triangle definitions follow from the unit-circle definitions. This makes the unit-circle definitions consistent with the definitions they replace (we might say the new definitions are “backward-compatible”).

So rather than the unit-circle definitions being proved from the right-triangle definitions (which can’t be done, because the latter don’t define the sine of obtuse angles in the first place), they are instead shown to be consistent with the latter, and then can be used even for acute angles. In the same way, a new version of software on your computer can be put in place of the old one as long as it still does the same things the old one did, even though it can now do more. That is what “backward compatibility” means.

Is there anything special about quadrantal angles?

The angles Mario is concerned about are called quadrantal angles, meaning that they lie exactly on the axes that divide the quadrants of the plane, and therefore are not actually in any quadrant. (I’m not entirely happy with the term, but I live with it. I think of it as “quarter-turn angles”.)

I’ll say a little more to your specific question about “quadrantal angles”, though. We can show that the trig functions of 0 radians and of π/2 radians are the limits of the “right-triangle-based” trig functions as the angle approaches 0 or π/2 respectively. For instance, if angle A of a right triangle is very small, the ratio of the opposite side, a, to the hypotenuse, c, is very small; and as the angle gets smaller, this ratio (the sine of the angle) gets smaller, approaching 0 in the limit. This is consistent with the sine function being a continuous function. (On the other hand, the tangent function is not continuous at θ = π/2, but this is consistent with the right-triangle observation that as angle A approaches 90 degrees with the adjacent side b fixed, side a increases without limit.)

These concepts (limits, continuity) are taught in calculus, usually after trigonometry; but they should make sense when understood informally. Here is a picture of the idea, as a triangle approaches a line segment along the positive x-axis:

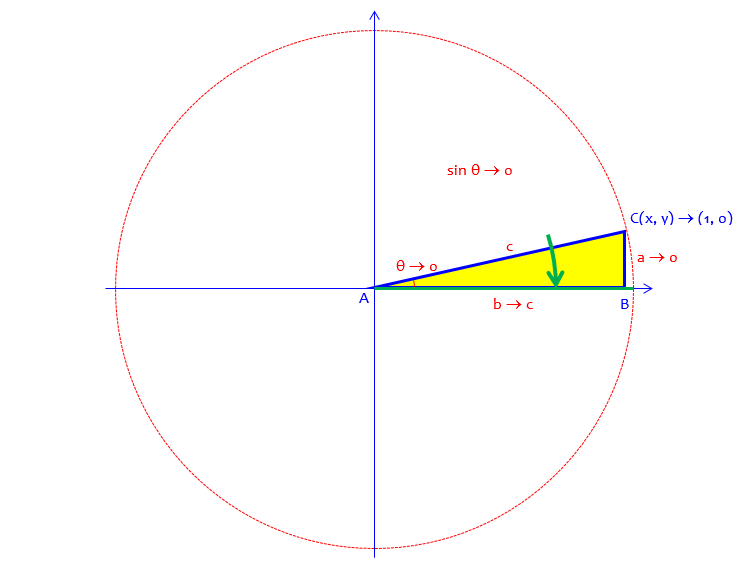
Leg a approaches zero as the angle approaches zero, while hypotenuse c stays the same, so the sine approaches zero. Similarly, leg b approaches the same value as c, so the cosine approaches 1.

This shows that if we want our extended definition of the sine to be continuous (informally, not making sudden jumps), then the sine of 0 has to be 0, and the cosine of 0 has to be 1. That adds more support to the unit-circle definition, though the latter is still a definition, not a theorem.

Explaining continuity with an example

Mario replied,

Interesting. So what if I were to say this if one of my classmates asked me the same question I did:

“Sure, the values of the trig functions can be evaluated using a right triangle. But remember, the cosine and sine functions also represent the (x, y) values of periodic motion, such as the position of a Ferris wheel cart on the perimeter of a Ferris wheel as it operates. The periodic motion exists at the points in which we can’t draw a right triangle on the unit circle. However, the periodic motion exists at those (x, y) values, and since the trig functions describe periodic motion, then the trig functions can have values at those points.”

Would that be right?

This turns the idea of a continuous function of the angle into a continuous function of time, which is easier to imagine; if the Ferris wheel moves smoothly, then it should move just the same through each point shown:

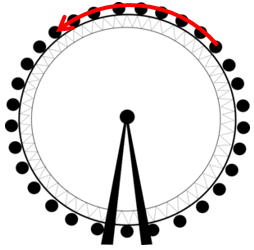
There is nothing special about the very top, or the rightmost point, or anything else. So there will be a value for the sine (height) and for the cosine (horizontal position) at those points too. Really, though, it’s not so much that the functions are periodic, as that they are continuous, that is important. There are no sudden jerks in our Ferris wheel.

Doctor Rick responded,

I don’t see anything wrong with what you’ve written. Would it convince your hypothetical classmate? Perhaps.

Let me take a new approach and examine this Ferris wheel example further. The horizontal and vertical distances of a cart from the center of the wheel, along with the radius to the cart, form a right triangle; the ratio of the vertical distance (the opposite side of the triangle) to the radius is the sine of the angle formed by the cart, the center, and the horizontal.

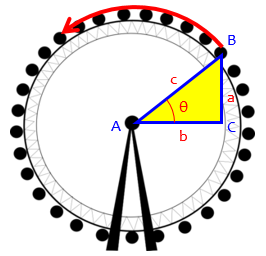
It sounds like you have no trouble with cases where the right triangle is not in the first quadrant — where the cosine or the sine, or both, is negative. You have expressed doubt only about quadrantal angles, when the horizontal, vertical, and radius do not form a triangle in the usual geometrical sense. What they form instead is a degenerate triangle, in which one side has zero length. Even though triangles in geometry cannot have zero-length sides, we can still talk about them and apply the “right-triangle definitions” of the trig functions, obtaining reasonable results.

A degenerate object in geometry is one that doesn’t fit the technical definition of that type of object, but to which formulas can still be applied – it’s just “on the edge” of the definition. For example, a line segment is a degenerate rectangle with height 0, and its area can still be found as length time width (equal to zero), even though it is not really a rectangle.

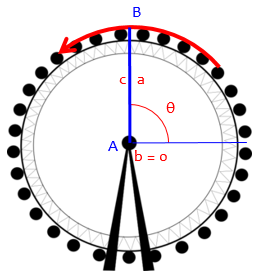
If we do not allow ourselves to do this, then as you say, we find ourselves unable to describe the continuous motion of the Ferris wheel; the description is interrupted at the quadrantal angles, though we can see that the motion itself is not interrupted! So, since (1) using degenerate triangles causes no problems, and (2) not allowing them does cause a problem, we go ahead and define the trig functions (sine and cosine, at least) for all angles.

I think this perspective might be helpful.

Mario concluded,

Yes, it is helpful! Thank you! I had to work at it a bit, but I got it.

That’s all we can ask!