One-sided limits of a composite function

(A new question of the week)

A good way to develop a sense of what limits are and how they work comes from working with visual representations of them, in the form of graphs. In particular when the functions are defined by graphs rather than by equations, we have a lot more flexibility in creating a problem, and can produce special cases that would otherwise be hard to create. Today’s question, from late February, is about a relatively obscure case, namely one-sided limits of a composite function.

Limits of a composite function

Here is the question, from Drey:

Given the following graphs of g and h, find the right side limit and left side limit of f(x) = (h o g)(x) in x = 1.

Provided solution:

lim _x–>1^– f(x) = -2

lim _x–>1⁺ f(x) = 0

What I did:

f(x)=(h o g)(x) meaning f(x)=g(x)*h(x)

Analyzing the graph I can see that lim _x–>1 g(x) = 1 and lim _x–>1 h(x) = 4. Could you give me tips on what should I do next?

The problem asks for the left-hand and right-hand limits of the composite function \(f=h\circ g\) at \(x=1\). Drey has correctly read the (left-hand) limits of g and h at 1 as 1 and 4; but he has misread the problem as to what f means, so the latter is irrelevant.

Drey had previously asked about some very different problems that involved limits of composite functions, for which Doctor Rick had provided a link to

Limit of Composite Function

The theorem stated there says,

Let \(f\) and \(g\) be real functions.

Let:

\(\displaystyle\lim_{y→\eta}f(y) = l\)
\(\displaystyle\lim_{x→\xi}g(x) = \eta\)

Then, if either:

Hypothesis 1: \(f\) is continuous at η (that is \(l = f(\eta)\))

or:

Hypothesis 2: for some open interval I containing ξ, it is true that \(g(x) ≠ \eta\) for any \(x\in I\) except possibly \(x = \xi\)

then:

\(\displaystyle\lim_{x→\xi}f(g(x)) = \lim_{y→\eta}f(y)\)

That is, if either the outer function f is continuous at the relevant point, or the inner function is non-constant near the relevant point, the limit of the composite function is just the limit of the outer function evaluated at the limit of the inner function. We can safely just substitute: $$\lim_{x→a}f(g(x)) = \lim_{y→\lim_{x→a}g(x)}f(y)$$ (The link demonstrates the need for at least one of the hypotheses to be true. The second is true for our problem.)

Doctor Rick answered:

Hi, Drey.

Are this and your previous pair of limit problems from a course? There is a connection between them, in that I related those problems to a theorem about limits of compositions of functions, and this problem also deals with limits and composition.

The difference is that the functions in this problem do not have (two-sided) limits at the relevant points, but only one-sided limits. It is not a big jump to see how the same idea can be used with one-sided limits; but we need to think carefully about which “side” of each limit we use.

We will be extending the previously stated theorem (or the thought that it embodies) to one-sided limits.

What is a composite function?

Before we can get there, however, it appears that you are confused about what a composition of functions is. You say

f(x) = (h o g)(x) meaning f(x) = g(x)*h(x)

but this is what the product function (hg) is, not the composition h ∘ g. The composition of h and g is defined as

(h ∘ g)(x) = h(g(x))

for all x in the domain of g such that g(x) is in the domain of h.

Also you say that from the graph you find

lim _x–>1 g(x)=1 and lim _x–>1 h(x)=4

Did you really mean this? What I see is that for g, for instance,

lim_x–>1^– g(x) = 1

lim_x–>1⁺ g(x) = 3

Perhaps you meant to put in minus signs on both of your limits.

Drey found limits (actually one-sided) of both functions at \(x=1\), which would have been appropriate for the product function \(hg\), in which both are evaluated for the same input; for the composite function \(h\circ g\), we’ll be evaluating the limit of one at the limit of the other, rather than at the same place.

A different example

We often demonstrate how to solve a problem by solving a similar one, to leave the “patient” ready to do their own.

Now, in order to help you understand how to solve your problem, I’m going to solve a different problem with the same functions. Let’s find

lim_x–>1^– (g ∘ g)(x)

As I mentioned, this means

lim_x–>1^– g(g(x))

Looking at the “inside” function g, as x approaches 1 from the left, g(x) approaches 1 from above — g(x) is greater than 1 to start with, and decreasing toward 1. And this g(x) is the argument of the “outside” function g, which therefore approaches 1 from the right.

Therefore, letting u = g(x), what we want is

lim_x–>1^– g(g(x)) = lim_u–>1⁺ g(u) = 3

Does that make sense? Give your problem a try based on this idea, and show me your work. Then I will see whether you are getting the idea, and if not, I might see what you are missing, so I can explain that part more carefully.

Here is a picture of what he did (observe that, because g is being used twice here, I am using two copies of the graph of g):

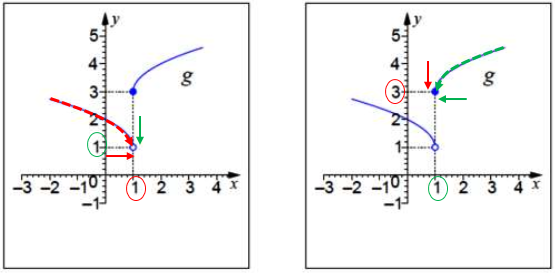
On the left, looking at the inner function g, the red arrow shows how x is approaching 1 from the left; following the broken red curve, we see that y decreases to 1 (the green arrow).

On the right, we see what is happening in the outer function g. There, the green arrow shows x (which was the y for the inner function) decreasing to 1, and following the broken green curve, we see y decreasing to 3 (the red arrow). So the limit is 3.

That is, as x approaches 1 from the left, \(g(x)\) approaches 1 from the right, and therefore \(g(g(x))\) approaches 3 from the right (from above).

The original problem solved

Drey responded,

Hello Doctor Rick.

Yes, this and the previous pair of limits are part of a course.

I gave the problem a try and I managed to understand how to find

lim_x–>1^– g(x) = 1

lim_x–>1⁺ g(x) = 3

In order to find f(x) I did f(x) = lim_x–>1^– f(u) where u = 1 from lim_x–>1^– g(x) = 1

Well I don’t know how to explain it but the only value that goes to 1 in the x axis and seems to be decreasing is -2 so

lim_x–>1^– f(u) = -2

now for  lim_x–>1⁺ f(u) where u =3 from lim_x–>1⁺ g(x) = 3 so f(3) seem to be increasing as x approaches 3  so the result is 3.

That’s what I got.

He has the right limits for the outer function in his problem, g. Then he actually gets the right answers, but appears to be guessing. We need to remove the guessing!

The answer explained in detail

Doctor Rick answered,

Hi, Drey. You said:

In order to find f(x) I did f(x) = lim_x–>1^– f(u) where u = 1 from
lim_x–>1^– g(x) = 1

Well I don’t know how to explain it but the only value that goes to 1 in the x axis and seems to be decreasing is -2 so lim_x–>1^– f(u) = -2

You got the correct answer, but I cannot follow your explanation. I know, you said you don’t know how to explain it — and it is indeed hard to talk about.

Let’s assume he had the right ideas, but needs help saying them. What are the parts of his explanation that don’t work?

First, f(x) is not a limit; it is just f(x) = (h ∘ g)(x). What you meant in the first line above is that you’re trying to find the left-hand limit of f(x) as x approaches 1.

When you then put f(u) in the limit expression, I don’t think f belongs there — it ought to be h. Then you say, “where u=1”; that doesn’t make sense as it stands: we can’t put a fixed number there — something has to be varying. Likewise, we can’t say that -2 is a “value that goes to 1 …”; -2 doesn’t go anywhere!

We need to carefully distinguish limits from actual function values, and variables from specific numerical values. In part, this is why the terminology of limits was invented: to make it possible to talk about what the ideas of calculus mean!

Introduce suitable notation

So, how can we talk about this in a way that makes sense? Let’s try to find a way – we might be inventing some notation along the way.

We are evaluating

lim_x–>1^– h(g(x))

I don’t know if you’re being taught the limit theorem I showed you for the previous problems as a formal theorem or more intuitively, but the conclusion of that theorem said (using our function names) that

If lim_y–>η h(y) = L and lim_x–>ξ g(x) = η, then

lim_x–>ξ h(g(x)) = lim_y–>η h(y)

This theorem needs to be modified to deal with one-sided limits, by considering from which side each limit above is taken. We know that we want to find the left-hand limit of h(g(x)) as x approaches 1, so the ξ above should be replaced by 1^–, and we start by finding (just as in my example)

lim_x–>1^– g(x) = 1

But we need to know from which side g(x) approaches 1. As I noted in the example, as x comes in toward 1 from the left, g(x) comes down toward 1 from above. So let’s invent a notation as a way to say that:

lim_x–>1^– g(x) = 1⁺

We normally use the superscript sign only in stating what the input approaches (and from what direction). But this seems like a reasonable notation, as long as we keep in mind that “1⁺” is not an actual number, but a description of a motion. It is what we will be writing in the limit statement to follow.

It is not uncommon that inventing a notation is a useful step in problem-solving. In George Pólya’s famous book How to Solve It, one piece of advice under the first step, Understand the Problem, is “Introduce suitable notation.” Doing so helps us to communicate with ourselves about the problem, and subsequently to others. The same is true of a picture or other graphic representation of the problem.

If we were writing a formal proof, we would probably make a precise definition of this notation; but in informal thinking, we just need to be sure we know what it means. As we’ll see, it is really a visual concept as we apply it to the graph.

The left-hand limit

Now we know that the limit of h that we need is as y = g(x) approaches 1 from the right (1⁺):

lim_y–>1⁺ h(y) = ?

Looking at the graph of h(x), we see that as x (the argument of h as shown on the graph) approaches 1 from the right, the curve comes down to the limiting value of -2. Thus,

lim_y–>1⁺ h(y) = -2

and we have

lim_x–>1^– (h ∘ g)(x) = lim_y–>1⁺ h(y) = -2

That’s the answer you got!

Here is a picture of what we’ve done here, like the picture above (this time including the two different functions):

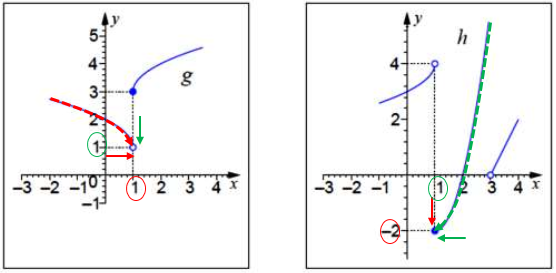
As before, on the left, looking at the inner function g, the red arrow shows how x is approaching 1 from the left; following the broken red curve, we see that y decreases to 1 (the green arrow).

On the right, we see what is happening in the outer function h. There, the green arrow shows x (which was the y for the inner function) decreasing to 1, and following the broken green curve, we see y decreasing to -2 (the red arrow). So the limit is -2.

That is, as x approaches 1 from the left, \(g(x)\) approaches 1 from the right, and therefore \(h(g(x))\) approaches -2 from the right (from above).

The right-hand limit

now for  lim_x–>1⁺ f(u) where u =3 from lim_x–>1⁺ g(x) = 3 so f(3) seem to be increasing as x approaches 3  so the result is 3.

Again, it doesn’t make sense to say that f(3) increases – f(3) is just a fixed number. But using my notation, we want to find

lim_x–>1⁺ h(g(x))

so we first find

lim_x–>1⁺ g(x) = 3⁺

(because, on the graph of g(x), as x comes in toward 1 from the right, the curve comes down toward 3). Thus the last step is

lim_y–>3⁺ h(y) = 0

which is not what you got. Perhaps you didn’t see that g(x) approaches 3 from above, so that the y above approaches 3 from the right. If you thought that y approached 3 from the left, then you also didn’t notice that on the graph of h(x), h(y) increases toward some unspecified limit (maybe infinity?) as x approaches 3 from the left.

These are tricky. I hope you have another problem like this that you can show me, with your work, so we can see if you have gotten the idea yet.

Again, here is a picture:

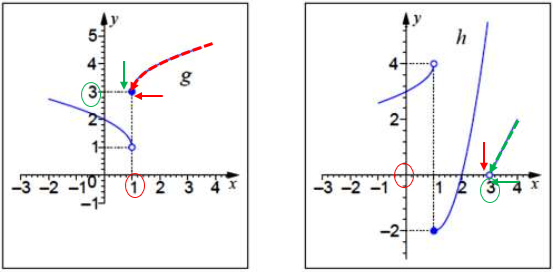
On the left, the red arrow shows how x is approaching 1 from the right; following the broken red curve, we see that y decreases to 3 (the green arrow).

On the right, we see what is happening in the outer function h. There, the green arrow shows x (which was the y for the inner function) decreasing to 3, and following the broken green line, we see y decreasing to 0 (the red arrow). So the limit is 0.

That is, as x approaches 1 from the right, \(g(x)\) approaches 3 from the right, and therefore \(h(g(x))\) approaches 0 from the right (from above).

We now have both a written notation and a visual procedure for solving these. Drey didn’t reply again (to this thread), so we trust that it worked.