Last week we looked at some questions about multiplication that arise once students learn to multiply fractions or decimals. Let’s turn to the underlying question: How do you multiply fractions, and why do we do it that way? How does cancelling fit in?
What does it mean?
Our first question is from 1999:
Meaning of Multiplying Fractions I am doing an essay assignment, and I got stuck on this question: What does it mean to multiply a fraction by a fraction? My sister and I think multiplying a fraction by a fraction just means to multiply a fraction by a fraction! Please help.
I answered, using pictures to connect multiplication of fractions to multiplication of whole numbers:
Hi, Mary.
Well, what does it mean to multiply a whole number by a whole number?
Two times three means the total of two groups of three things; here are two groups of three squares:
+-------+-------+-------+
| | | |
| | | |
| | | |
+-------+-------+-------+
| | | |
| | | |
| | | |
+-------+-------+-------+
So 2 times 3 is 6.
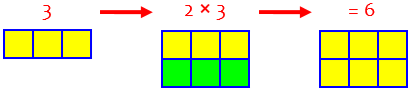
(One nice thing about this rectangle model of multiplication is that it makes it easy to see that we could also call it three groups of two things!)
Now what does it mean to multiply a fraction times a whole number?
One half times six means half a group of six; here's half a group of three squares:
+-------+-------+-------+
| | | |
+-------+-------+-------+
: : : :
:.......:.......:.......:
1/2 times 3 is 3/2, because I've cut the squares into six halves, of which I'm keeping three.

I made three squares in the row, then cut the whole row in half, leaving 3 half-squares, or 3/2. We can also rearrange that into 1 1/2 squares; we’ll be looking at such mixed numbers later!
We do the same thing to multiply a fraction times a fraction; here's half a group of 2/3 of a square:
+-----+..:
| : | :
+-----+..:
: : : :
:..:..:..:
1/2 times 2/3 is 2/6, because by cutting the square into two slices one way and three the other way, I have six pieces, of which I'm keeping only two.
So a fraction times anything is just that fraction OF that amount; break it into as many pieces as the denominator says, and keep as many of them as the numerator says.
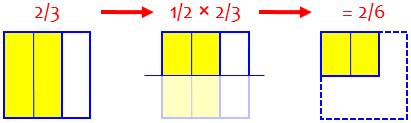
I cut the square into 3 parts vertically and kept only two columns, making 2/3; then I cut that in half horizontally, making 2/6. We’ll be going through this process more slowly in a moment, and also how to change the answer to 1/3.
Why we multiply numerators and denominators
Next, consider a somewhat different question from earlier the same year:
Multiplying Fractions I have trouble multiplying fractions. Could you help me?
This time the question is about how to do it, rather than what it means; but I chose to start with the meaning rather than the routine method that Derek likely was having trouble with:
Hi, Derek. Rather than just remind you that to multiply two fractions you multiply the numerators and the denominators, let's think it through. Suppose I have half a cake left over from my birthday, and want to take 2/3 of it. First I'll cut the half into thirds. If I had cut the whole cake into pieces this size, there would have been twice as many pieces (6), so the pieces are each one sixth of the whole cake. Now I want to take two of these pieces; that make 2/6 of a cake, or 1/3. So 2/3 of 1/2 is 1/3. You can see it even more easily if you reverse it: 2/3 of 1/2 is the same as 1/2 of 2/3. Half of two thirds is one third.
Pictures are coming in a moment, but this last comment is of interest. From working with whole numbers (as in the \(2\times 3\) example above, we know that multiplication is commutative; that is, you can change the order and get the same result. Doing the same thing with fractions sometimes makes the work easier, as it does here. Since half of 2 items is 1 item, half of 2 thirds is 1 third, and we’re done!
Now the pictures; we’ll make half a cake, and then take 2/3 of that in a way that we could do with any pair of fractions:
Here's a picture of how it works. I first cut the cake in two from top to bottom, and take one half:
+--+--+
|//| |
|//| |
|//| |
|//| |
|//| |
+--+--+
Now I'll cut that half into three pieces; while I'm at it, I'll cut the part I didn't take at the same time, showing that these pieces are really sixths:
+--+--+
|//| |
+--+--+
|//| |
+--+--+
|//| |
+--+--+
Now I'll take two of the three pieces:
+--+--+
|XX| |
+--+--+
|XX| |
+--+--+
|//| |
+--+--+
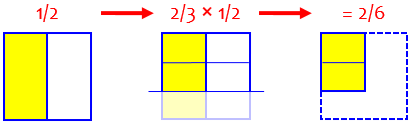
There are 6 equal parts of the whole cake (even though half of those didn’t exist when we did the cutting), and we have 2 of them, so the result is \(\frac{2}{6}\).
The two pieces I've taken are the product of the numerators of the fractions 2/3 and 1/2: 2 * 1 = 2.
1
+--+
|XX|
2 +--+
|XX|
+--+
The six pieces the whole cake was cut into are the product of the denominators of the fractions: 3 * 2 = 6.
2
+--+--+
| | |
+--+--+
3 | | |
+--+--+
| | |
+--+--+
So the pieces I've taken are 2/6 of the cake:
2 1 2 * 1 2
--- * --- = ----- = ---
3 2 3 * 2 6
There's the answer yet again!
This explains why the product of the fraction is found by multiplying the numerators (to find the numerator of the result), and multiplying the denominators (to find the denominator of the result). That is the basic rule we need to follow, whether or not we remember why: $$\frac{2}{3}\times\frac{1}{2} = \frac{2\times 1}{3\times 2} = \frac{2}{6}$$
Canceling first
But wait! There’s more!
Now there's one more thing to add: often you will have to simplify the answer (as in this case, which turns it into 1/3), and there's a way to make that easier. What we do is to simplify before we actually multiply. Just notice that when I wrote out the multiplied fraction above,
2 * 1
-----
3 * 2
both numerator and denominator contain a 2. I can rearrange this as
2 * 1 2 1 1 1
----- = --- * --- = 1 * --- = ---
2 * 3 2 3 3 3
You can do this very easily by just crossing out the 2's, which is called cancelling:
/
2 * 1 1
----- = ---
3 * 2 3
/
In plain text, we had to indicate crossing out with a separate slash; we’d normally write it like this: $$\require{cancel}\frac{2}{3}\times\frac{1}{2}=\frac{2\times 1}{3\times 2}=\frac{\bcancel{2}\times 1}{3\times\bcancel{2}}=\frac{1}{3}$$
In more complicated problems, this can save a lot of work, since otherwise you would have to multiply, then factor or divide, undoing part of your work. I hope this helps a little. If I haven't helped with whatever is the hardest part for you, please write back and give me an example of a problem you find hard and how you tried to do it; that will help me see where you need the most help.
We didn’t get a reply, but more examples follow!
More about cancelling
Let’s dig into that idea of cancelling, with this question from 1998:
Cancelling Fractions How do you cancel 3 2 - x - ? 5 3 The book I have explains it, but it looks like teachers from Planet X are writing it. I totally don't get the entire problem. HHHHHEEEEELLLLLPPPPP!
This time, the whole point is canceling; the example is very much like the last one. (We’ll see harder ones later.)
Doctor Otavia answered this time, offering advice about reading textbooks, then giving a similar example:
Hi, Lori! I also sometimes find math textbooks hard to understand. If I don't understand a part the first time I read it, I usually reread it and try some of the examples, and sometimes that helps. Let's take a look at a problem that's like your problem. Once you understand how to do this kind of problem, you should be able to do yours in a jiffy. Let's use oh... how about 7 13 --- * --- = ? 3 7 Those seem like good numbers to me. After all, this is just an example so you can learn the method for solving problems like these.
This is nearly identical, except for the specific numbers.
What you want to do is find the product of those two fractions, right? And you want to use cancellation to help you do that. So, how do you multiply fractions together? You multiply the numerators (the top part) and you multiply the denominators (the bottom part), so the first step would look like
7 13 7 * 13
--- * --- = --------.
15 7 15 * 7
So far, it looks just like regular old fraction multiplication. So where's the cancellation? Well, we know that 3 * 7 = 7 * 3 [the commutative property], so we can rewrite our fraction, which then looks like
7 * 13 7 * 13
-------- = --------.
15 * 7 7 * 15
Now, we can again rewrite that fraction as a product of two fractions, so now we have
7 * 13 7 * 13 7 13
-------- = -------- = --- * ---- .
15 * 7 7 * 15 7 15
But wait, 7/7 means 7 divided by 7 which is 1, right? So what we really have is
13
1 * ----.
15
But we know that anything times 1 equals itself, so your answer is 13/15.
This is the l-o-n-g way! Though this explains why we can “cancel”, we’d never write all that out.
A shorter way and a bigger example
So, that's a step-by-step method for finding the products of fractions using cancellation along the way, and now that you've seen it, I'll show you a shorter way, but first I had to explain the whole reasoning behind it, or else the simpler explanation might not make sense!
Let's say you have some fractions you want to multiply together. Imagine that when you do the first step of combining the numerators and the denominators, you have a fraction that looks like
6 * 11 * 2 * 5
---------------- .
2 * 6 * 10 * 7
An easy way to cancel stuff is to just get rid of any numbers that you have in both the numerator and the denominator. The reason this works is that what you're really doing is rearranging the numbers and then expressing the fraction as a product of **something that's really one in disguise** times whatever is left, or in this case, since you have a 6 in the numerator and a 6 in the denominator, you can just throw out both 6's - and the same goes for the 2. What you're left with is
11 * 5
-------- .
10 * 7
So, rather than write out the rearrangements, we can just imagine that we did, and write the results. Wherever we have the same number on the top and the bottom, we would be able to gather them into a single fraction that is equal to 1, and they disappear:
$$\frac{6}{2}\times\frac{11}{6}\times\frac{2}{10}\times\frac{5}{7} = \frac{6\times 11\times 2\times 5}{2\times 6\times 10\times 7} = \frac{\cancel{6}\times 11\times \bcancel{2}\times 5}{\bcancel{2}\times \cancel{6}\times 10\times 7} = \frac{11\times 5}{10\times 7}$$
But sometimes common factors are hidden:
Looks like you're done, right? No, not quite yet. Because see, 10 = 5 * 2, so really the fraction is equal to
11 * 5
-----------.
2 * 5 * 7
Now you can again cancel out the 5, and your final result is
11 11
------- = ----.
2 * 7 14
So I guess another way to describe cancellation is to multiply the numerators and the denominators, (in other words, combine all your fractions into one big fraction), and then factor every number as much as you can. Once you've done this, every number that appears in the numerator and in the denominator can be thrown out, or cancelled.
We can either explicitly write out the factors, as she did,
$$\frac{11\times 5}{10\times 7} = \frac{11\times 5}{2\times 5\times 7} = \frac{11\times \cancel{5}}{2\times \cancel{5}\times 7} = \frac{11}{2\times 7} = \frac{11}{14}$$
or we can just divide by the common factor, replacing each number with the quotient:
$$\frac{11\times 5}{10\times 7} = \frac{11\times \overset{1}{\cancel{5}}}{\underset{2}{\cancel{10}}\times 7} = \frac{11}{2\times 7} = \frac{11}{14}$$
Cross-cancelling
Students often hear the term “cross-canceling”, and sometimes get confused about it. Here’s a 2001 question:
Multiplying Fractions I need help on how to solve this: 8 * 3 - - 9 5 My teacher said something about cross-cancelling, but I didn't understand. Can you please explain? Thanks.
Doctor Rick answered:
Hi, Alysha. You know the basic method for multiplying fractions, right? You multiply the numerators, and that's the numerator of the product. Multiply the denominators, and that's the denominator of the product. Let's do that, but DON'T do the multiplications yet - just write them where they go. 8 3 8*3 - * - = --- 9 5 9*5 Now, to reduce the fraction to lowest terms, we want to look for a common factor in the numerator and denominator. By not multiplying first, we make this job easier: we have already done some factoring of the numerator and denominator. I'll finish the factoring, but keep the factors together to show where they came from: 8*3 (2*2*2)*3 --- = --------- 9*5 (3*3)*5
The idea of not doing the multiplications yet is actually what all of us have been doing so far, without pointing it out. We do that because it makes visible what is really happening so that we can pause to think about how to make the work easier. I often advise students to first write what they are going to do (in this case, the numbers to be multiplied), then think, and then do it. Even if you don’t change what you actually do, you’re showing your teacher what you are doing (in case you make a mistake), and you are showing yourself what you are claiming to do, so you can check that you really did it!
Here, we know we’ll want to look for common factors in order to simplify the final result, so why multiply and then immediately un-multiply! Now we’re looking in the smaller numbers 8, 3, 9, and 5, rather than the products 24 and 45 we would otherwise have had to work with. And that lets us see what we can do next:
Now you can see a common factor: 3. We can "pull them out" of the fraction: 8*3 (2*2*2) 3 --- = ------- * - 9*5 (3)*5 3 But 3/3 = 1, so all that's left is 8*3 (2*2*2) 8 --- = ------- = -- 9*5 (3)*5 15 That's the answer. What we call "cancelling" is really "pulling out" the same number in the numerator and denominator, making a factor of 1, as I did above when I pulled out a factor of 3/3.
All of this is what we’ve done in previous examples, without explicitly seeing it as “cross-canceling”.
Now we can talk about "cross-cancelling." Notice that the 3 in the numerator came from the 3 of 8*3, while the 3 in the denominator came from the 9 of 9*5. In other words, the 3 in the numerator was from the numerator of the second fraction, 3/5, while the 3 in the denominator was from the denominator of the first fraction, 8/9.
So in what we did, without having to notice it, we canceled the numerator of one with the denominator, canceling diagonally, and that is what is called “cross-canceling” – something that you don’t even have to notice in order to do.
Again, he did it the long way to demonstrate why it can be done. We can just imagine some of the steps, knowing what they allow us to do:
You don't need to write nearly as much as I did. You can just look at the problem 8 3 - * - = ? 9 5 and visualize it like this: 8 * 3 ----- = ? 9 * 5 Then look for common factors in one number of the numerator and the other number of the denominator. We see that 3 is a factor of both 3 (in the numerator) and 9 (in the denominator). Divide each of these numbers by 3 (on paper, you'd cross out the 3 and write a 1 above it, and cross out the 9 and write a 3 below it): 8*1 --- = ? 3*5 You can look again for other common factors. Do the 8 and 5 have a common factor? No. Therefore we're done, and the product is 8*1 8 --- = -- 3*5 15
Again, our work on paper would look like this: $$\frac{8}{9}\times\frac{3}{5} = \frac{8}{\underset{3}{\cancel{9}}}\times\frac{\overset{1}{\cancel{3}}}{5} = \frac{8}{15}$$
Do you see why it's called cross-cancellation? You look for common factors in these pairs:
8 3
\ /
__ \/ __
/\
/ \
9 5
It's possible you might find common factors vertically, too - between the 8 and 9, or between the 3 and 5. But if you did, it would mean that the fractions you started with weren't in lowest terms. If the fractions are in lowest terms, then you only need to look for common factors in the "cross-terms."
By the way, students often ask about “cross-multiplication”, which is used in solving proportions, and also, with a quite different meaning, as a shortcut for adding fractions; and they confuse all of these with “multiplying across”, a term used for the basic idea of multiplying fractions, which goes straight across rather than diagonally. Because of all this confusion, I prefer not to use the word “cross” in most of these settings.
A big example
We’ll close with this 2008 question:
Canceling and Reducing When Multiplying Several Fractions I need help when multiplying three or more fractions. I know how to cancel diagonally when the fractions are right next to each other. I know how to cancel the numerator and denominator of a fraction, too. I have seen people cancel using the numerators and denominators that aren't near each other. How do they do that? Can you double cancel a number? How do you keep it all straight then? Thanks a million for your help!
Doctor Ian answered:
Hi Renee, The key idea is that multiplication is commutative. Suppose you have something like 4 3 25 - * -- * -- 5 10 30 You can break everything into prime factors, 2*2 3 5*5 --- * --- * ----- 5 2*5 2*3*5 Now, to multiply fractions, we just multiply the numerators and denominators separately, right? So this is the same as 2*2 * 3 * 5*5 ----------------- 5 * 2*5 * 2*3*5
Again, we’re seeing it as one big fraction, even if we never write it that way!
So now, we're just reducing a fraction. And we can do that by identifying prime factors that appear in both the numerator and denominator:
2 * 3 * 5*5
----------------- Cancel a 2
5 * 5 * 2*3*5
3 * 5*5
----------------- Cancel another 2
5 * 5 * 3*5
5*5
----------------- Cancel a 3
5 * 5 * 5
1
----------------- Cancel two 5's
5
So the result of the multiplications is 1/5. Does this make sense so far? Remember that when you "cancel" two identical numbers you are making each number into 1. That's why there is a 1 left in the numerator after all the numbers that were there have canceled.
The key is that we can cancel matching factors anywhere in the numerator and the denominator. But we don’t have to write all the factors; as I showed above, we can just divide by common factors:
Here's how I'd do it in practice: 4 3 25 - * -- * -- Our original problem. 5 10 30 2 3 25 - * -- * -- I canceled a 2 from the 4 and the 10. 5 5 30 1 3 25 - * -- * -- I canceled a 2 from the 2 and the 30. 5 5 15 1 3 5 - * -- * -- I canceled a 5 from the 5 and the 25. 1 5 15 1 3 1 - * -- * -- I canceled the two 5's. 1 1 15 1 1 1 - * -- * -- I canceled a 3 from the 3 and the 15. 1 1 5 1 1 1 - * -- * -- Nothing left to cancel. 1 1 5 As I said, the key idea is that since the numerators and denominators are going to get multiplied anyway, it doesn't matter whether the common factors are next to each other, or far away. What I'm doing here is realizing that I really have one big fraction that I need to reduce, rather than three fractions that I need to multiply.
If we write this work out as one big pile, we see the “double cancellation” Renee asked about, where we cancel the result of a cancellation:
$$\frac{4}{5}\times\frac{3}{10}\times\frac{25}{30} = \frac{\overset{2}{\cancel{4}}}{5}\times\frac{3}{\underset{5}{\cancel{10}}}\times\frac{25}{30} =\\ \frac{\overset{\overset{1}{\cancel{2}}}{\cancel{4}}}{5}\times\frac{3}{\underset{5}{\cancel{10}}}\times\frac{25}{\underset{15}{\cancel{30}}} = \frac{\overset{\overset{1}{\cancel{2}}}{\cancel{4}}}{\underset{1}{\cancel{5}}}\times\frac{3}{\underset{5}{\cancel{10}}}\times\frac{\overset{5}{\cancel{25}}}{\underset{15}{\cancel{30}}} =\\ \frac{\overset{\overset{1}{\cancel{2}}}{\cancel{4}}}{\underset{1}{\cancel{5}}}\times\frac{3}{\underset{\underset{1}{\cancel{5}}}{\cancel{10}}}\times\frac{\overset{\overset{1}{\cancel{5}}}{\cancel{25}}}{\underset{15}{\cancel{30}}} = \frac{\overset{\overset{1}{\cancel{2}}}{\cancel{4}}}{\underset{1}{\cancel{5}}}\times\frac{\overset{1}{\cancel{3}}}{\underset{\underset{1}{\cancel{5}}}{\cancel{10}}}\times\frac{\overset{\overset{1}{\cancel{5}}}{\cancel{25}}}{\underset{\underset{5}{\cancel{15}}}{\cancel{30}}} = \frac{1}{5}$$
Renee replied,
Thanks a lot Dr. Ian! I actually understand the concept for the first time! Realizing that it's all really just one BIG fraction comprised of prime factors - and you're actually reducing as you go along rather than just at the end...sure makes sense to me now. Whoaaa, you're good!

Pingback: Multiplying Fractions by Whole or Mixed Numbers – The Math Doctors
Pingback: Dividing Fractions: Can You Picture It? – The Math Doctors