Multiplying Fractions by Whole or Mixed Numbers

Last week we looked at how to multiply fractions, and why we do it that way. But what do we do when one of the numbers is a whole number, or when one or both are mixed numbers? And do we have to do it the way we are taught?

Fraction × whole: Put it over 1

We’ll start with this basic question from Joy in 1995:

What is 4/5 x 10?

What is the answer to this fraction?

Here the problem is 4/5 x 10. Please explain.

Doctor Ken answered, offering the method that usually feels most comfortable to beginners:

When I multiply fractions, I like to write _both_ of the numbers as fractions.  So I would take your problem and notice that 10 = 10/1, so we have

  4            4   10
  - x 10 =     - x --
  5            5    1

Any whole number can be written this way; \(\frac{10}{1}\) means 10 pieces, each of which is a whole.

Then we have to remember how to multiply two fractions.  When we multiply two fractions together, we multiply everything in the top together, and then everything in the bottom together.  Then we take what we get and put it in a new fraction.  So we get 

  4   10    4 x 10
  - x -- =  ------  
  5    1    5 x  1

What we have here are 40 pieces, each of which is a fifth:

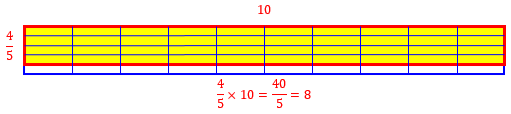
This, of course, is just what we did last week. As we saw, we could do the multiplications and call the answer \(\frac{40}{5}\) and then just do the division to get the answer, 8; but, as we also saw last week, we can simplify before multiplying:

This, technically, is our answer, but we can make it simpler in a couple of ways.  First, notice that 5 x 1 = 5.  So we can write the fraction as 

  4 x 10    4 x 10
  ------ =  ------
   5 x 1      5

Now we do the tricky part.  Notice that 10 = 2 x 5.  So let's replace 10 in the top by 2 x 5, to get

  4 x 10    4 x 2 x 5
  ------ =  ---------
    5           5


Now when we have the same thing in the top as we do in the bottom, we can cancel them both out, but (this is very important) we can only do it when the top and bottom each have multiplication separating the parts, not addition or subtraction or anything else!!  So if the top had been 4 + 2 + 5, we wouldn't have been able to cancel anything.  In this case though, we're fine.  So we get

  4 x 2 x 5   4 x 2
  --------- = ----- = 4 x 2 = 8.
       5        1

This is an important part that wasn’t mentioned last week: Some students get so used to “canceling” that they do it everywhere, even when the two numbers are not in a numerator and a denominator, or when they are being added rather than multiplied. I often have to remind students, “Only cancel factors” or “Only cancel top with bottom”.

So the answer to our problem is 8.  This may seem like a lot of work, but if you do it enough, you'll get really good at it, and you'll start doing it in your head.  To let you know what you have to look forward to when you get good at these, when I looked at this problem, I knew the answer in less than a second!

This, too, is important: You don’t usually write all the steps. But it will be important to write every step that you might get wrong, based on your own experience. I call this “driving defensively”.

Fraction × whole: Multiply on top

For a slightly different perspective on the same type of problem, consider this question from a few months later:

Multiplying Fractions and a Whole Number

Right now I'm multiplying fractions and whole numbers. It's kind of hard to give an example. I'll try to give you some.

When you ask for help, it’s a good idea to show both the specific kind of problem you are working on, and where you get stuck. We will often do a similar example if you provide one of your own, but seeing where you struggle can help us design our examples to illustrate the point you need work on.

Doctor Sydney first asked for clarification of the type of problems Ethan wanted, then continued, picking an example to demonstrate:

Hello, Ethan!  

Sorry it took a while for me to get back to you--I've not been at the computer for a few days!

Okay, well I'm glad we've found examples of the kinds of problems you are working on, but I'm not sure exactly where you are having problems.  So, why don't we do an example problem, okay?

How about the problem:

   3
  --- x 4 = ?
   5

When you are multiplying a fraction and a whole number, all you do, is multiply the numerator of the fraction (the number on top) by the whole number, and put that number over the denominator (the number on bottom). So, for this problem, we would simply multiply 3 by 4 and put it over 5. Since 3 times 4 is 12, our answer would be 12/5  (You may want to simplify this into a compound fraction; write back if you aren't sure how!).  Does that make sense?

If you noticed in the previous answer that the 1 on the bottom didn’t really do anything, then you were thinking well! We used that method mostly to show why the whole number ends up multiplying the numerator; once you realize that, you can skip writing the 1 and just write the whole number on top.

I have sometimes described this in terms of a house: The numerator is the ground floor (first floor in America), while the denominator is the basement. A whole number, on the ground outside, is nominally at the same level as the ground floor, and can walk right in, despite the appearance of front steps.

Here’s the work: $$\frac{3}{5}\times 4=\frac{3\times 4}{5}=\frac{12}{5}$$ We covered converting between improper fractions like this and mixed numbers, in the post

Improper Fractions and Mixed Numbers: Converting

In this case, we would divide 12 by 5, getting a quotient of 2 and a remainder of 2. The remainder is the number of extra fifths, so the answer is \(2\frac{2}{5}\):

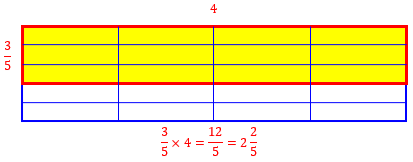
Here is another thing to think about when you are doing these problems -- when would you multiply a fraction by a whole number in real life?  Can you think of examples where this would be useful?  What if you and 4 other friends got a pizza so that each of you wanted 1/5 of the pizza.  If the pizza has 8 slices, how can you figure out how many slices of pizza each of you should get?

That’s actually a tricky one! You each get \(\frac{1}{5}\) of 8 pieces, so you multiply: $$\frac{1}{5}\times 8=\frac{1\times 8}{5}=\frac{8}{5}=1\frac{3}{5}$$ pieces. Have fun cutting them! (In practice, I’d give each person 1 piece, leaving 3 more pieces; then I’d cut \(\frac{3}{5}\) from each of them to give to A, B, and C, leaving \(\frac{2}{5}\) of each of the 3 pieces; then I’d give one of those and half of the last to D and E. Or maybe I just let them fight over it.)

Fraction × mixed number: Use improper fractions

Moving on to mixed numbers, here is a question from 1996:

Multiplying Fractions

I don't know where to begin.  I need help with problems such as this one:

        3 1/4 x 3/4 = 

I'm trying to get my G.E.D. and I'm stuck on fractions so if you have anything on fractions that could help me do them easier I would really appreciate hearing about them.

Doctor Syd answered:

Hello, Dennis!

We're glad you wrote.  Fractions can be very tricky, indeed.  My 23-year-old sister still grumbles about having to learn fractions, in fact!  But if you can learn a few strategies, things will go much more smoothly.  

I will write fractions in the form p/q, with the slanted bar, in this message, but when you do it, it will be easier to see if you can write the fractions with a horizontal bar...

We generally write fractions using the “slash” to make typing easier, but it’s worth mentioning that the horizontal bar makes it easier to keep track of what you are doing. I have seen students who wrote all fractions by hand like \({}^2{\mskip -4mu/\mskip -3mu}_3\), which interfered with multiplying.

Writing the mixed number as an improper fraction

We’ll be rewriting our mixed number as an improper fraction; the post mentioned above shows how to do this, but Doctor Syd put it all in his answer:

Okay...In problems where you are asked to multiply two fractions together, the best strategy is to get both fractions into the form p/q.  How do we write 3 1/4?  Well, 3 1/4 means we have 3 + 1/4 of whatever we have, right?  And, 3 = 3/1 So, how do we add these two fractions?  We find a common denominator!  

The least common denominator of two numbers is the smallest number such that both numbers divide it.  So, in our case, the smallest number such that 1 and 4 divide that number is just 4, right?  So, we want both of the fractions we are adding up to have a 4 in the denominator.  

To get a 4 in the denominator of the 3/1 fraction, we multiply by 4/4 which is just 1, so this should not change the number.  So, 3 = 3/1 * 4/4.  To multiply two fractions together, you just multiply the numbers in the numerators (the numbers above the division line) and the numbers in the denominators (the numbers below the division line).  So, in this case we get that 3 = 3/1 * 4/4 = 12/4

Now we are ready to figure out this:

  3 + 1/4 = ?

We can now rewrite this as:

  12/4 + 1/4 = ?

To add two fractions with the same denominator, you just add the numbers in the numerator and keep the denominator the same.

So, 12/4 + 1/4 = 13/4. 

Thus our answer is 13/4.

In summary, we did this: $$3\frac{1}{4}=3+\frac{1}{4}=\frac{3}{1}+\frac{1}{4}=\frac{3\times 4}{1\times 4}+\frac{1}{4}=\frac{12}{4}+\frac{1}{4}=\frac{12+1}{4}=\frac{13}{4}$$ We’ll look at a quicker way soon.

Multiplying

Now we have to multiply \(\frac{13}{4}\times\frac{3}{4}\):

So, back to the original problem (stick with me, here!  I know the explanation may seem long, but after you practice these methods on some problems it will be much better, I guarantee!)

To find out what 3 1/4 * 3/4 is, we rewrite the problem as:

  13/4 * 3/4

Now, we've already practiced multiplying two fractions of this form, so follow that procedure, and you should get your answer!

Finishing up: $$\frac{13}{4}\times\frac{3}{4}=\frac{13\times 3}{4\times 4}=\frac{39}{16}=2\frac{7}{16}$$

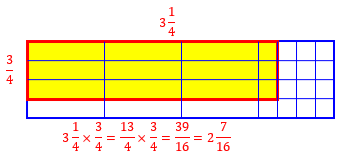
Mixed × mixed: Doing it faster

What if they’re both mixed numbers? Consider this 1998 question:

Multiplying Mixed Numbers

Could you please explain how to multiply fractions? For example:

   2 4/7  x  5 1/6 

Thank you, Devon Dunphy

I answered this one, using the same method and then explaining some extra features:

Hi, Devon. Fractions can be a lot of fun once you've made friends with them, but they can be a little scary when you first meet them. These two look pretty ugly, so we'd better straighten them up before we try to work with them. In order to give you a chance to practice with your own problem, I won't do exactly your problem, but one like it:

  2 3/7 x 3 2/3

We’ll see a better reason to “straighten up” the mixed numbers than just to make them less scary; but we’ll also see that we can just tough it out and leave them as they are, if we are brave enough.

Writing as an improper fraction the quick way

I first showed the long way as we saw it before:

To make them look neater, we first change the mixed numbers into improper fractions. You probably remember how to do that. You want to turn 2 3/7 into some number of sevenths, so you remember that 2 is just 14 sevenths, and add them:

      3    14     3    17
   2 --- = --- + --- = ---
      7     7     7     7

The same way,

      2     9     2    11
   3 --- = --- + --- = ---
      3     3     3     3

But you don’t have to write all that out:

Note: When you're used to it, you can try my way, which is to start at the denominator, multiply by the number clockwise from it (the whole number) and add the next number clockwise (the numerator). This way, we get:

   3 x 3 + 2 = 11

by following the arrow:

   +-------->
   |   + 2 -> 11
   | 3  ---   --
   |   x 3 ->  3
   +-----

But that's just a trick to avoid extra writing.

Multiplying

Okay, so regardless of how you change the mixed numbers into improper fractions, our problem is really:

   20    11
   --- x ---
    7     3

Now how do you multiply fractions? The "rule" says you multiply the numerators to get the numerator of the product, and you multiply the denominators to get the denominator of the product:

   a   c   a x c
   - x - = -----
   b   d   b x d

So in this case, we multiply 20 x 11 and 7 x 3:

   20    11    20 x 11   220
   --- x --- = ------- = ---
    7     3     7 x 3    21

I had chosen an example that wouldn’t involve canceling; Devon’s problem does.

Often, you'll find something to cancel out to put the result in lowest terms; I recommend doing that before you actually multiply anything, to save work. In this case, we don't find anything to cancel, so we'll try the cancelling trick in the next example.

I followed this by explaining the rule using pictures, for an example of multiplication of two proper fractions, much like what we did last week, including canceling. Here is Devon’s: $$\require{cancel}2 \frac{4}{7}\times 5 \frac{1}{6}=\frac{18}{7}\times \frac{31}{6}=\frac{\overset{3}{\cancel{18}}}{7}\times \frac{31}{\cancel{6}}=\frac{93}{7}=13\frac{2}{7}$$

Can you do it without improper fractions?

Now for a different perspective, from 2003:

Multiplying Mixed Numbers

Why can you not multiply mixed numbers without changing them into improper fractions? 

I understand that it is easier and I understand the process, but is there a theory?

When someone asks, “Why can’t I do it this other way?”, I generally suggest they try and see. They will either discover why it’s a bad idea, or find that it can be done. This one, though, might be a lot to ask a student to discover for herself.

Doctor Douglas answered:

Hi Natasha,

Thanks for writing to the Math Forum.

You can indeed multiply mixed numbers without converting them to improper fractions.  

  3 1/2 x 4 1/5 = (3 + 1/2) x (4 + 1/5) 
                = (3 x 4) + (1/2 x 4) + (3 x 1/5) + (1/2 x 1/5)
                = 12 + 2 + 3/5 + 1/10
                = 14 + 6/10 + 1/10
                = 14 7/10

Here we wrote the mixed numbers as sums and distributed, multiplying each term of the first number by each term of the second. We can illustrate what is happening with a picture:

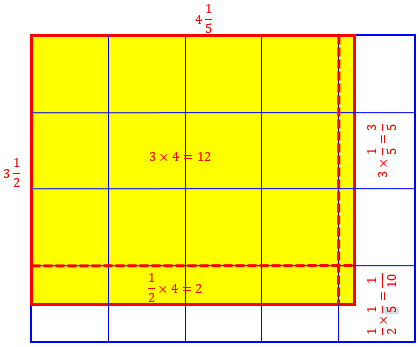
Here, we multiplied the whole parts, \(3\times 4=12\); and the first fraction times the whole, \(\frac{1}{2}\times 4=\frac{4}{2}=2\); and the whole times the second fraction, \(3\times\frac{1}{5}=\frac{3}{5}\); and the two fractions, \(\frac{1}{2}\times\frac{1}{5}=\frac{1}{10}\). Then we added: $$12+2+\frac{3}{5}+\frac{1}{10}=14+\frac{6}{10}+\frac{1}{10}=14\frac{7}{10}$$

Doing it this way (multiplying all the terms out using the distributive property of multiplication over addition) was probably more work than converting:

  3 1/2 x 4 1/5 = 7/2 x (21/5)
                = (7 x 21)/(2 x 5)
                = 147/10
                = 14 7/10

Here we had just two multiplications instead of four multiplications and three additions of fractions. Definitely easier! On the other hand, the numbers got bigger.

But there might be situations where doing the conversion is more work.  For example, we could have the following situation: let there be two years where some monetary quantity increases by 2% the first year and decreases by 2% the following year. Then the total overall percentage change is

  (1 + 2%)(1 - 2%) = (1 + 2/100)(1 - 2/100)
                   = 102/100)(98/100)
                   = (102 x 98)/(100 x 100)
                   = 9996/10000
                   = 0.9996

or a 0.04 % drop overall. Notice how we had to execute the multiplication 102 x 98.

This time, the numbers got considerably bigger!

We could also have done the following:

  (1 + A)(1 - A) = 1x1 + A - A - AxA
                 = 1 - AxA
                 = 1 - (0.02)(0.02)
                 = 1 - 0.0004
                 = 0.9996

which is a lot easier in terms of the number crunching, especially if we don't have access to a calculator. So there may be times where the conversion of a mixed number to a fraction may not be the most efficient way to proceed.

Here he used some algebraic thinking to come up with a shortcut. And that shortcut involved the distributive method. We could also write this out without the algebra: $$\left(1+\frac{2}{100}\right)\left(1-\frac{2}{100}\right) = 1-\frac{2}{100}+\frac{2}{100}-\frac{4}{10000} = 1-\frac{4}{10000} = \frac{9996}{10000}$$

Are improper fractions necessary?

We’ll close with a very similar question from 2004:

Multiplying Mixed Numbers

Why do you need to convert mixed numbers to improper fractions before multiplying them together?

I teach 5th grade mathematics, and the children asked me about this. We understand that you have to do it, but what is the mathematical theory behind this operation?  I have looked in numerous math resources and cannot find an explanation.

Of course, what they’re expecting is an explanation of why the improper fraction method is valid and valuable. But as we now know, there are two sides to the question. I answered:

Hi, Jane.

This is an excellent question!

Like many things in math, converting to improper fractions isn't really NECESSARY, just CONVENIENT (though you might not think so until you finish reading this!).

Call it relatively convenient. Students often don’t realize that the hard work we teach is easier than the harder work we don’t teach! So it’s good from time to time to teach the harder work. Here, I’ll make a point not quite made in that last answer:

You can multiply mixed numbers directly if you want, just the same way you multiply whole numbers.  The key is the distributive property: to multiply a sum, you can multiply each part of the sum and then add.  With whole numbers, this looks like

  25 * 32 = (20 + 5)*32
          = 20*32 + 5*32
          = 20*(30 + 2) + 5*(30 + 2)
          = 20*30 + 20*2 + 5*30 + 5*2
          = 600 + 40 + 150 + 10
          = 800

The routine multiplication algorithm, which older generations were just told to do because it was right, is now taught with more emphasis on the reason; but I imagine many students still don’t really understand what’s going on. An occasion like this, where a class has asked “why”, is a chance to point out many connections.

This is really what we are doing when we write

    32
  * 25
  ----
   160 <-  5*32
   64  <- 20*32
  ----
   800

Multiplying digit by digit is really just distribution, hidden by the notation.

With mixed numbers, you can do the same thing if you want:

  (2 1/2)*(1 1/5) = (2 + 1/2)*(1 + 1/5)
                  = 2*(1 + 1/5) + 1/2*(1 + 1/5)
                  = 2*1 + 2*1/5 + 1/2*1 + 1/2*1/5
                  = 2 + 2/5 + 1/2 + 1/10
                  = 2 + 4/10 + 5/10 + 1/10
                  = 2 + 10/10
                  = 3

You could write this something like this:

     2 1/2
  *  1 1/5
  --------
      1/10 = 1/10
      2/5  = 4/10
    2 1/2  = 5/10
  ---------------
    2       10/10 = 3

Here, as I did each multiplication, I put fractions in one column and whole numbers in another, then I added the (one) whole number, and rewrote the fractions with common denominator 10 and added them, then converted to a whole number.

Or, you can convert to improper fractions:

  5/2 * 6/5 = (5*6)/(2*5) = 6/2 = 3

Now why is this so much easier?  It's because when you mix multiplication and addition, you have to use the distributive property, which gives you a lot of parts to add up.  When you mix multiplication with pure fractions (no addition), everything works out neatly because fractions are the same thing as division, and multiplication and division are just different sides of the same operation.  So mixed numbers, which are sums, work well when you want to add or subtract; while pure fractions, which are divisions, work well when you want to multiply or divide.  We convert to whatever form works best for what we want to do.

I often say that fractions and multiplication “play well together”, because they are from the same family. And that’s also why we often teach multiplication and division of fractions before we tackle addition and subtraction.