Last time we looked at what improper fractions (and, to some extent, mixed numbers) are. There are many situations where we need to rewrite one of these forms as the other – mixed numbers are most convenient for talking about numbers in real life, while improper fractions are easiest for doing operations like addition. Let’s look at some questions about those conversions.
From improper to mixed
We’ll start with a question from 1997:
Fractions, Improper Fractions, Mixed Numbers How do you turn an improper fraction into a mixed number? John
Doctor Reno answered, starting with some important advice:
Thanks for asking us for help, John. Once you truly understand what fractions are, it will become very easy for you to change improper fractions into mixed numbers! Just remember that *all* fractions are handled in the same way, whether they are "improper" or not. I know you probably would like me to just give you some "rules" for doing this, but I have found it difficult to memorize all the "rules" in math. It is much easier for me to think about what I know about numbers so that I don't have to memorize stuff. When you memorize, you can easily forget the rules. When you understand a topic in math, when you know what is really going on, you *can't* forget what to do! My answer will take a while, though, so sit back with some paper and a pencil, relax, and enjoy!
Many people who are good at math (including basic arithmetic) agree: If math is just about memory, then it can be forgotten. When it is based on understanding, it will last. (I have to work to remember a stranger’s name; a friend, I just know!)
So, what is a fraction? Essentially, it is a division:
The word fraction comes from an old Latin word that means "broken". Fractions break 1 of something (like an apple, a cake) into pieces, any number of pieces we need to break it into. Regular numbers are "whole", they are unbroken. So we can think of fractions as parts of whole numbers, or parts of whole things. A half is what we have when we *divide* a whole into two pieces. A half, then, is 1 divided by 2. A third is 1 divided by 3. We don't even do the division, we just say the fraction. Instead of saying and writing "1 divided by 3", we say one-third, and we write 1/3. We don't need to do the division, because fractions can be manipulated, or used, as if they are the answer! We can add 1/3 to other numbers, or multiply it, or subtract or divide it. We have also just learned in the paragraph above that the "/" symbol is a shorthand way of saying or writing "divide". This will help us a lot when we work with fractions.
This is why, when we type math, we can write “\(1\div 3\)” as “\(1 / 3\)“, or even as “\(\frac{1}{3}\)“. And thinking of a fraction as a division will help in understanding what comes next.
We need to know how to change improper fractions to mixed numbers because it is a lot easier for people to understand a mixed number than an improper fraction. For example, isn't it easier for you to understand me when I tell you that I have 3 candy bars than if I tell you that I have 6/2 candy bars?
This is the main motivation for converting in this direction; we are usually taking a form that was useful for calculating, and writing it so it makes sense to our “customer”.
Let's look at the improper fraction 22/3. This means that some objects have been divided into thirds, and that we have 22 of these pieces in front of us. But it's difficult for me to know *exactly* what 22/3 means! Let's say we're talking about chocolate bars. It will be easier for me to know how much candy I have if 22/3 is changed to a mixed number. There are several ways to figure out what it means. Let's take a look at 3 ways. One way is to remember that 3/3 makes one whole: if we have cut a candy bar into three pieces, those three pieces together are the whole candy bar. We can then subtract 3 pieces from the 22 pieces of our 22/3 and we have 1 whole plus 19 pieces left over: 1 19/3. If we do this again, we find that we have 2 whole candy bars and 16 pieces left over: 2 16/3. And if we do this *again*, we see that we have 3 whole candy bars and 13 pieces left: 3 13/3. We can do this and do this until we find that we have 7 whole candy bars with 1 piece left over.
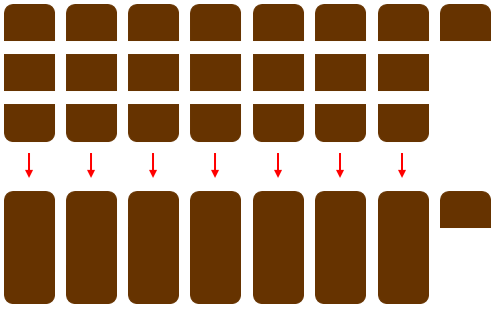
So we could just keep pulling out groups of 3 until we have 7 piles of 3 (each pile meaning one candy).
But this takes a long time, doesn't it? It would be a big help if we could find a quicker way to do this! Well, we could use our knowledge of arithmetic again to help us out. 22/3 = 21/3 + 1/3. And we know that 21/3 = 7 (21 divided by 3 is 7). And we then find that 22/3 is 7 whole candy bars with 1 piece (1/3) left over. But even *this* method can take a long time, can't it?
Here we recognized that the largest multiple of 3 less than 22 is 21, and that that is 7 times 3.
The easiest method of all is to divide 22 by 3. Remember, we can do that because the "/" means divide. We did it in the paragraph above. 22 divided by 3 is 7 with 1 left over. The only thing we have to be careful about is to remember exactly what that left over 1 means. It means 1 piece of a candy bar that has been cut into 3 pieces. Therefore, the 1 actually means 1/3 of a candy bar. 22/3 = 7 1/3. Now that we understand fractions better, we can change *any* improper fraction into a mixed number! All we have to do is divide (and remember what the remainder means).
So we did a division with a remainder; the quotient is the whole part of the mixed number (the number of wholes, each of which is 3 third), and the remainder, 1, is the number of additional thirds.
We’ll have several more ways to think about this, but this basic idea is at the root of them.
Cutting paper strips
The next question is from 1999:
Fractions and Decimals I have to make 17/11 a proper fraction, and I don't know how to do it.
You can’t really turn an improper fraction into a proper fraction; Brittney presumably means “mixed number”.
I replied:
The basic idea in this problem is that a proper fraction has to be less than one; that is, the numerator (top) must be less than the denominator (bottom). In 17/11, that isn't true, so you have to find a way to rewrite it as a mixed number so that the fraction part is proper.
That’s the goal. I used a physical example to build an understanding, using paper strips as Doctor Reno used candy bars:
Suppose I take a piece of paper and cut it into 11 equal strips. That gives me 11 elevenths. To get 17 elevenths, how many more do I need? Yes, 17 - 11 = 6. So I take another sheet of paper and cut it into elevenths, and take 6 of them. Now I have 17 elevenths. But I can also call it one whole sheet and 6 more elevenths: 1 6/11. That's the mixed fraction form for 17/11. What I did was to divide 17 by 11 and find that the result is 1 with a remainder of 6. That is, it took one whole sheet and 6 extra elevenths. That's how you solve this sort of problem: divide the numerator by the denominator, and use the quotient as the whole number part and the remainder as the new numerator (with the same denominator you started with).
Here, rather than start with a pile of pieces, I imagined trying to make 17 elevenths, 11 at a time. The division by 11 tells me I need 1 whole sheet, and the remainder tells me I will need 6 of the 11 pieces from an extra sheet.
Now we can do one without the image, just thinking of it as an abstract division:
Here's another example: what is 28/3 as a mixed number?
Divide 28 by 3 and you get 9 with a remainder of 1. So the 28/3 can be written as
1
9 ---
3
That is, if we group 28 thirds into groups of 3 (so that 3 thirds will make a whole), we get 9 groups (units) and 1 extra third.
Gluing boards together
We had a similar question two months later:
Improper Fractions I really need help on how to make an improper fraction into a mixed number.
I replied with actual “pictures”, this time starting with the pieces, but focusing on the division:
Hi, Priyana. Dr. Math to the rescue!
Let's look at an improper fraction this way: I'll give you 53 blocks of wood, and tell you that each piece is 1/6 of a board. How many boards did I use to make them?
+---+ +---+ +---+ +---+ +---+ +---+ +---+ +---+ +---+
| 1 | | 7 | | 13| | 19| | 25| | 31| | 37| | 43| | 49|
+---+ +---+ +---+ +---+ +---+ +---+ +---+ +---+ +---+
+---+ +---+ +---+ +---+ +---+ +---+ +---+ +---+ +---+
| 2 | | 8 | | 14| | 20| | 26| | 32| | 38| | 44| | 50|
+---+ +---+ +---+ +---+ +---+ +---+ +---+ +---+ +---+
+---+ +---+ +---+ +---+ +---+ +---+ +---+ +---+ +---+
| 3 | | 9 | | 15| | 21| | 27| | 33| | 39| | 45| | 51|
+---+ +---+ +---+ +---+ +---+ +---+ +---+ +---+ +---+
+---+ +---+ +---+ +---+ +---+ +---+ +---+ +---+ +---+
| 4 | | 10| | 16| | 22| | 28| | 34| | 40| | 46| | 52|
+---+ +---+ +---+ +---+ +---+ +---+ +---+ +---+ +---+
+---+ +---+ +---+ +---+ +---+ +---+ +---+ +---+ +---+
| 5 | | 11| | 17| | 23| | 29| | 35| | 41| | 47| | 53|
+---+ +---+ +---+ +---+ +---+ +---+ +---+ +---+ +---+
+---+ +---+ +---+ +---+ +---+ +---+ +---+ +---+
| 6 | | 12| | 18| | 24| | 30| | 36| | 42| | 48|
+---+ +---+ +---+ +---+ +---+ +---+ +---+ +---+
I can divide 53 by 6 to find out how many boards I can make by putting the blocks back together in groups of 6:
___8_
6 ) 53
48
--
5
The long division will become a visual tool in itself, as each part becomes part of the mixed number we are forming. And you don’t really have to do the whole long division by hand; you could use a calculator to divide 53 by 6, and just write down the whole part of the answer (8.83…) on top, then multiply that by the 6 to find how much 8 6’s is, and subtract to find how many left-over 6’s there will be.
This says I can make 8 whole boards, using 8x6 = 48 of the pieces, and I'll have 5 blocks left. Since each block is 1/6 of a board, that means I've made 8 5/6 boards:
+---+ +---+ +---+ +---+ +---+ +---+ +---+ +---+ +---+
| | | | | | | | | | | | | | | | | |
+---+ +---+ +---+ +---+ +---+ +---+ +---+ +---+ +---+
| | | | | | | | | | | | | | | | | |
+---+ +---+ +---+ +---+ +---+ +---+ +---+ +---+ +---+
| | | | | | | | | | | | | | | | | |
+---+ +---+ +---+ +---+ +---+ +---+ +---+ +---+ +---+
| | | | | | | | | | | | | | | | | |
+---+ +---+ +---+ +---+ +---+ +---+ +---+ +---+ +---+
| | | | | | | | | | | | | | | | | |
+---+ +---+ +---+ +---+ +---+ +---+ +---+ +---+ +---+
| | | | | | | | | | | | | | | |
+---+ +---+ +---+ +---+ +---+ +---+ +---+ +---+
\_____________________________________________/ \___/
8 boards = 48/6 5/6
This makes the quotient and the remainder visible; the latter is a number of sixths.
Now we can make a memorable visual image of the long division and the final answer:
The rule for changing an improper fraction into a mixed number is to divide the numerator by the denominator; the whole-number quotient is the whole number part of the answer, and the remainder is the numerator of the fraction part:
+------------------------+
| |
| 5 <--+ |
| ___8_----> 8 --- | |
6 ) 53 6 <--|---+
48 |
-- |
5 --------------+
The divisor, 6, becomes the denominator of the fraction part (because denominators are divisors); the quotient becomes the whole part; and the remainder, at the bottom of our work, moves to the top of the fraction, because that’s the number of left-over pieces.
From mixed to improper
How about reversing the process? Here is a question from one week earlier than the last one:
Converting Between Mixed Numbers and Improper Fractions I get mixed up doing and undoing improper and mixed numbers.
This time, the question asks for both directions. I answered, starting again with an image, this time of conversion from a mixed number:
Hi, Linday.
Let's take a simple example:
What is 1 1/2 as an improper fraction? We can picture it as a box and half a box:
+-------+ +-------+
| | | |
| | +-------+
| |
+-------+
If we turn the whole into halves, there are two halves there, plus the extra half makes 3:
+-------+ +-------+
| | | |
+-------+ +-------+
| |
+-------+
What we've just done is to rewrite 1 as 2/2, then add 2/2 + 1/2 to get 3/2.
You can think of this as making a common denominator, something we’ll be doing in a later post. Once the whole number is turned into a fraction, we can combine into one improper fraction.
In general, you multiply the whole part by the denominator, then add the numerator of the fraction part. One way to think of this is that you start at the "bottom" and move clockwise around the mixed number, multiplying by the whole, then adding the numerator:
+--------+
| |
| + 1 +-> 2 x 1 + 1 = 3
| 1 --- ---
| x 2 ----------------> 2
| |
+----+
Here’s a nicer picture: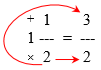 
Our eyes move clockwise around the mixed number, first multiplying and then adding, to make the numerator.
My advice for going the other direction was much like what we’ve seen:
To go the other way, let's start with the 3/2. How many wholes can we make out of 3 halves? Just divide the 3 by 2, because it takes 2 halves to make each whole; we get 1 with a remainder of 1. That means there is one whole, and 1 half left over:
+--------------+
| |
| __1_rem 1 |
2 ) 3 --- |
-2 2 <--+
So you just use the denominator (divisor) as the denominator with the remainder as the numerator.
Whole and partial pies
Here is a question from 2001:
Converting Mixed Numbers to/from Improper Fractions I have to change mixed numbers like 1 3/4 into improper fractions, and write fractions like 7/5 in simplest form by changing them to mixed numbers. I don't know how to do this.
Jo is again asking for both directions. Doctor Ian started with pictures you can interpret as pies (or maybe cakes):
Hi Jo, You can represent a proper fraction with a picture like this, +---+---+ |###| | +---+---+ 3/4 |###|###| +---+---+ right? Well, you can represent a unitary fraction with a similar picture: +---+---+ |###|###| +---+---+ 4/4 = 1 |###|###| +---+---+ So if you have something like 2 3/4, you can represent it this way: +---+---+ +---+---+ +---+---+ |###|###| |###|###| |###| | +---+---+ +---+---+ +---+---+ |###|###| |###|###| |###|###| +---+---+ +---+---+ +---+---+ and now you can just count the #'s: +---+---+ +---+---+ +---+---+ |###|###| |###|###| |###| | +---+---+ +---+---+ +---+---+ = 11/4 |###|###| |###|###| |###|###| +---+---+ +---+---+ +---+---+
So a “unitary fraction”, representing 1, is a whole “pie”; and if you draw the picture, converting a mixed number to an improper fraction is just a matter of counting pieces.
Of course, it's a hassle to draw pictures, so you can do the same thing with numbers:
4 3/5 = 4 + 3/5
= 1 + 1 + 1 + 1 + 3/5
= 5/5 + 5/5 + 5/5 + 5/5 + 3/5
= (5 + 5 + 5 + 5 + 3)/5
= (4*5 + 3)/5
This last line looks almost like a formula, doesn't it? It's just the same numbers arranged in a different way. I'll bet that if you were to work enough examples like this, you could probably convince yourself that you can convert any mixed fraction into an improper fraction this way:
A + B/C = (A*C + B)/C
That’s the routine method I’ve shown: multiply whole by denominator, add the numerator, and put that over the same denominator.
Of course, if you just try to remember the formula without understanding (from practice) why it works, you might get it mixed up. So you want to be careful not to try to 'memorize' the formula.
This is our common theme: Don’t depend on memory alone.
He, too, followed up with the other direction:
Now, what about going the other way? Well, again using pictures, suppose we have a fraction like 25/6. We can start breaking 25 items into groups of 6:
##### ##### #####
##### ##### ### ##### ### ###
##### = ##### + ### = ### + ### + ### = ...
##### ####
#####
\__________/ \________________/
25 19 + 6 13 + 2(6)
Eventually, you end up with
### ### ### ###
# + ### + ### + ### + ###
\__________________________/
1 + 4(6)
Do you see how this corresponds to the picture that you would draw for the fraction 4 1/6?
Here we were given a collection of 25 things that want to become sixths; so we gather them together by sixes, which turns out to mean division:
Again, you can do this with numbers instead of pictures, which speeds things up:
25/6 = 19/6 + 1
= 13/6 + 2
= 7/6 + 3
= 1/6 + 4
And eventually it would occur to you to notice that if you divide 25 by 6, you get 4 remainder 1, which is to say,
___
6 ) 25 = 4 remainder 1 = 4 + 1/6
The rule: \(\displaystyle\text{quotient}+\frac{\text{remainder}}{\text{divisor}}\).
But again, if you just try to remember this 'method', you're likely to get mixed up under pressure (for example, when you're taking a test). The safest thing to do is to work it out the long way until you find yourself jumping ahead to the answer because you know what it's going to turn out to be.
This is sometimes the best way to really learn something: Do it the hard way until your mind insists on taking the shortcut, because it feels natural.
Negative mixed numbers
We’ll close with a special case that comes up mostly when you are learning algebra:
Converting Negative Mixed Numbers to Improper Fractions During the process of converting a negative mixed number into an improper fraction, I noticed that we do not pay any attention to the rules of adding negative and positive numbers. For example: -4 1/7 = -4 X 7 + 1 = -28 + 1 = -29/7, not -27/7 Why is this so? The rules of adding integers don't seem to apply. Shouldn't the final answer be -27/7?
Brenda was trying to mechanically apply the rule we have been discussing, without thinking carefully about meaning: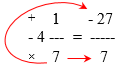 
Doctor Ian corrected that:
Hi Brenda,
The rules apply just fine, once you realize that the mixed number
a b/c
is an abbreviation for
(a + b/c)
So
-4 1/7
means
-(4 + 1/7)
= -(28/7 + 1/7)
= -(29/7)
= -29/7
What we have here is a case where the order of operations collides with a special notation. (This is part of the reason we avoid using mixed numbers in algebraic equations!) The space between whole and fraction here is taken to imply addition, rather than multiplication as it is in algebra; but this addition takes precedence the way multiplication usually does: The mixed number \(4\frac{1}{7}\) has to be thought of as a unit, to the whole of which the negation applies: \(-4\frac{1}{7}\) means \(-\left(4\frac{1}{7}\right)\). Given that fact, there is nothing new here.
It's exactly the same thing that happens with decimals, because decimals ARE mixed numbers:
-3.29
= -3 29/100
= -(3 + 29/100)
The negative sign on a number applies to the entire number, not just to the first digit.
The negative can’t move
Here is a 2004 question about a similar issue:
Placement of the Negative Sign in a Negative Mixed Number When you have a negative improper fraction, does the negative sign automatically distribute throughout your fraction? For instance, is -1 3/5 the same as 1 -3/5 and 1 3/-5? We have an intuitive sense that the fractions are equal, but we are having trouble proving it. If this is true, why is it the case? Your help is much appreciated! Julia and Sam
I replied, focusing on the notation:
Mixed numbers don't play well with negative signs, or with algebraic notation in general. When we write 1 3/5, we really mean (1 + 3/5), and the negative -1 3/5 means -(1 + 3/5), which distributes as -1 + -3/5 So -1 3/5 = -(1 + 3/5) = -8/5 1 -3/5 = 1 - (3/5) = 2/5 1 3/-5 = (1)(3/-5) = -3/5 Or at least that's how I would interpret each expression if I came across it out of context! Only the first contains cues that strongly suggest a mixed number is intended, since we never write mixed numbers with negative fractional parts.
Actually, if I saw these written normally, as \(-1\frac{3}{5}\), \(1\frac{-3}{5}\), and \(1\frac{3}{-5}\), I might take the last two both as multiplication at first glance; but I’d want to ask their author what was intended!
Generally, it's better to use improper fractions instead of mixed numbers in algebra, to avoid not only that source of confusion, but also something like 1 3/5 x, where the first space means addition, the second means multiplication, and parentheses have to be supplied.
Pingback: 2020 and the Y0K Problem – The Math Doctors