The next topic in our survey of fractions is the fact that two different fractions can represent the same number – that is, they can be equivalent, though they are written differently. At first, this may seem strange to students: the number 5 only has one “name”, so why should 1/2 and 2/4 be different “names” for the same number? But in fact, this is part of what makes fractions so useful. Before we look at how to “reduce” or “simplify” a fraction, we’ll consider some questions about the mere fact that two different fractions can be equal.
Renaming a fraction
Here is a question from 2000:
Renaming Fractions I don't understand how you rename fractions. Can you help me? Thank you. Alyssa
I answered, using pictures:
Hi, Alyssa.
Let's start with a simple fraction, 1/2. That means we've taken something, say a block, and cut it into two (the denominator) equal pieces, and then taken one (the numerator) of them:
+---------+---------+
|XXXXXXXXX| |
|XXXXXXXXX| |
|XXXXXXXXX| |
|XXXXXXXXX| |
|XXXXXXXXX| |
|XXXXXXXXX| |
+---------+---------+
The whole block represents the “unit” (the number 1, one block), and the “shaded” part is half of it, the number \(\frac{1}{2}\), just as two shaded blocks would represent the number 2.
Now, if I cut each of those pieces in half, I'll have a total of 4 pieces, of which I've taken 2:
+---------+---------+
|XXXXXXXXX| |
|XXXXXXXXX| |
|XXXXXXXXX| |
+---------+---------+
|XXXXXXXXX| |
|XXXXXXXXX| |
|XXXXXXXXX| |
+---------+---------+
By cutting the whole in half crosswise, I’ve cut each of the original pieces in the same way, so we have doubled the number of equal parts, as well as the number of pieces shaded.
In other words, the fraction 1/2 is the same as 2/4; they are two names for the same amount. We call these equivalent fractions. Do you see how I changed 1/2 to 2/4? I just had to multiply both the numerator and the denominator by 2, since there are twice as many pieces in all, and I took twice as many of them. I could just as well have divided the pieces in thirds, to make a different fraction:
+---------+---------+
|XXXXXXXXX| |
|XXXXXXXXX| |
+---------+---------+
|XXXXXXXXX| |
|XXXXXXXXX| |
+---------+---------+
|XXXXXXXXX| |
|XXXXXXXXX| |
+---------+---------+
Now I've rewritten 1/2 as 3/6, by multiplying numerator and denominator by 3, so that I have 3 out of 6 pieces. Here's a list of equivalent fractions:
1 2 3 4 5 6 7 8
--- = --- = --- = --- = --- = --- = --- = --- = ...
2 4 6 8 10 12 14 16
These fractions all represent the same quantity, \(\frac{1}{2}\). We found them by multiplying the numerator and denominator by 1, 2, 3, 4, 5, 6, 7, 8, and so on.
Now, we can also rename fractions in the opposite direction. If I DIVIDE both the numerator and the denominator of a fraction by the same number, then I get another name for the same fraction. For example, if you gave me the fraction 3/6, I would see that I could divide both 3 and 6 by 3, giving 1/2. By doing this, I have SIMPLIFIED (or REDUCED) the fraction; the smaller numbers are easier to work with, so this is a good thing to be able to do. You can always make the numbers bigger by multiplying them by something; but you can't always make them smaller, since two numbers are not always divisible by the same thing. If I can't divide them by anything, we say the fraction is "in lowest terms" - that is, we can't make the numerator and denominator any smaller. Our original 1/2 is in lowest terms, but 2/4 is not.
Renaming in both directions can be useful: We usually want a final answer to be in lowest terms (reduced) to make it easy to talk about; but while we are doing something with the fractions (such as adding them) we sometimes have a reason to use larger terms.
Equivalent fractions
Here is a 1999 question starting with a specific example that goes in that reverse direction:
Equivalent Fractions I am trying to understand equivalent fractions. Example: 6 1 -- = - 12 2
Understanding is important! Doctor Rick answered, again using pictures, but dividing the cake differently:
Hi, Sam. This is 6/12: +---+---+---+---+---+---+ |xxx|xxx|xxx|xxx|xxx|xxx| |xxx|xxx|xxx|xxx|xxx|xxx| +---+---+---+---+---+---+ | | | | | | | | | | | | | | +---+---+---+---+---+---+ The big rectangle is cut into 12 equal-sized boxes, and 6 are marked with x's. Each box is 1/12 of the whole, so 6 of them is 6/12.
That’s Sam’s first fraction; how about the other?
This is 1/2: +-----------------------+ |xxxxxxxxxxxxxxxxxxxxxxx| |xxxxxxxxxxxxxxxxxxxxxxx| +-----------------------+ | | | | +-----------------------+ The big rectangle is cut into 2 equal-sized boxes, and 1 is marked with x's. Each box is 1/2 of the whole.
These were both drawn with the same size “whole” in order to compare them.
Both pictures show the same space marked with x's. You could imagine the rectangle being a chocolate cake. If you cut it in 2 equal-sized pieces and eat one, you have eaten the same amount as if you cut it in 12 equal-size pieces and ate 6 of them. The two fractions are EQUIVALENT.
(So don’t imagine you’re eating less when you eat fewer pieces! Maybe they are also bigger.)
That’s the concept; but there’s more to be said:
How do you find equivalent fractions? Look again at that cake cut into two pieces. Make 5 vertical cuts, and you have cut the cake into 12 pieces. You multiplied the total number of pieces by 6, but you also multiplied the number of pieces you're going to eat by 6. The total number of pieces is the denominator. The number of pieces you chose is the numerator. You just multiplied the numerator and the denominator by the same number, 6. You could have made any number of vertical cuts and you'd get another fraction equivalent to 1/2. If you multiply both the numerator and the denominator by the same number - any whole number - you will get a fraction equivalent to 1/2. For instance, you can multiply by 2/2 to get 2/4; by 3/3 to get 3/6; by 4/4 to get 4/8, and so on.
This is what we did above, making equivalent fractions by multiplying both terms in the fraction. And, again, we can start with the bigger terms, too:
What about going the other way? Starting with 6/12, you can find some equivalent fractions by DIVIDING the numerator and denominator by the same number. But you can't just pick any number, as you can when you multiply. The numerator and denominator must both be DIVISIBLE by the number. Both 6 and 12 are divisible by 2, so one fraction equivalent to 6/12 is 3/6 (divide 6 by 2 and divide 12 by 2). Both 6 and 12 are divisible by 3, so another equivalent fraction is 2/4. Both 6 and 12 are divisible by 12, so another equivalent fraction is 1/2. But 1 and 2 have no common factors, so you cannot find a fraction equivalent to 1/2 by dividing. There is no equivalent fraction with smaller numbers. We say that 1/2 is IN LOWEST TERMS.
As I said to Alyssa, you can multiply by anything, but you can only divide by common factors. That’s why we have to stop eventually, in this case with \(\frac{1}{2}\).
Remember I said that 4/8 is equivalent to 1/2? Two fractions that are equivalent to the same fraction are equivalent to each other. This means that 4/8 and 6/12 are equivalent. But 6 is not a multiple of 4, and 12 is not a multiple of 8. So what's the rule?
We’ll soon be examining how to compare fractions; this example shows that you may not find all fractions equivalent to one of them, such as \(\frac{4}{8}\), by starting from the other, such as \(\frac{6}{12}\), and just multiplying its terms. But there is a way:
If you want to find ALL the fractions that are equivalent to 6/12, first reduce it to lowest terms: find the equivalent fraction that is in lowest terms. That's 1/2. Then multiply the numerator and denominator by each number, 1, 2, 3, 4, and so on, and you will have a list of ALL the fractions equivalent to 6/12. The list will go on forever, so don't try to write them all - but you know what they are. I've probably said more than you wanted to see. I hope it helps. If you have specific problems that you can't do, let us know - and tell us your wrong answer, that will help us figure out what you need to learn.
Presenting the concept to a class
One more question, from 2000:
Demonstrating Equivalent Fractions My daughter is a 5th grader in a gifted class. She has been given an assignment to teach other children in her class about equivalent fractions. The demonstration must last at least 10 minutes, and she must use visuals. She does not understand the concept well enough, she feels, to explain and demonstrate to others. I am trying to help her with a lesson plan that would be unique and simple so that she can learn as well as teach others her age. I have gone to various sites and am having a difficult time finding something I can explain to her and that she can use.
I answered:
Hi, Karen. One thing to do first is to go to our search page and enter the phrase "equivalent fractions". There your daughter will be able to look through examples of how we have explained the concept to others, which may give a number of different approaches to try - one of which may be just what she needs in order to feel more confident about it.
I’ve included the best such pages here; but the topic can also be found in answers about operations on fractions, such as addition.
I proceeded to adapt the visual approach we’ve already seen to her specific situation, trying to make it fun and memorable:
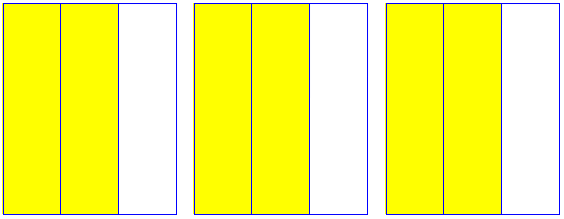
Here's my favorite way. Take a sheet of paper and divide it into some number of columns, and shade some of them in:
+---+---+---+
|XXX|XXX| |
|XXX|XXX| |
|XXX|XXX| |
|XXX|XXX| |
|XXX|XXX| |
|XXX|XXX| |
|XXX|XXX| |
+---+---+---+
Now make several copies of this, by hand or with a copier. Label the shaded part on the original "2/3" (in my example).
Now we have several very hands-on models of the same fraction, \(\frac{2}{3}\):
Now take one of the copies and draw a line across the middle
+---+---+---+
|XXX|XXX| |
|XXX|XXX| |
|XXX|XXX| |
+---+---+---+
|XXX|XXX| |
|XXX|XXX| |
|XXX|XXX| |
+---+---+---+
Suddenly the 2/3 has changed to 4/6! Write "4/6" on the shaded part. You could have fun with this and act like it's a magic trick, making the change behind a scarf. If someone puts the act down, saying nothing really changed, well, that's the whole point. Fractions aren't magic, they're just common sense.
I’m rather proud of this idea! By pretending that something has changed, we are calling the students’ attention to the fact that drawing one more line didn’t change the value, only its appearance.
Now ask someone in the audience if (s)he can see how to change the thirds (on another sheet) into ninths, or twelfths. After repeating this a few times, you will have a set of equivalent fractions taped to the board: 2/3, 4/6, 6/9, 8/12, and so on. These are all different ways to name the same fraction.
When you’re done, either you or others will have made a set of fraction cards like this:
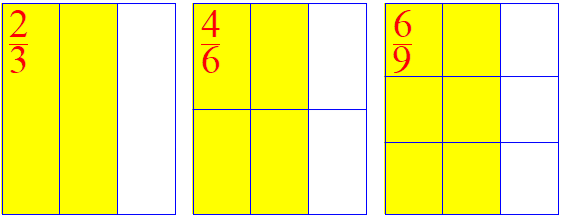
Now here comes the real math. Write on the board:
2 2 4
--- x --- = ---
3 2 6
This explains what the first equivalent fraction means: we have twice as many pieces in all (the denominator - which means "namer," since it says that each piece is a "third"); and also twice as many pieces in our fraction (the numerator - which means "numberer," since it tells how many of those pieces we have.) In multiplying both by the same number, we do not change the meaning of the fraction.
If the students have learned something about multiplication of fractions already, then this could be done as I stated it; if not, you’d want to write this as
2 x 2 4
------- = ---
3 x 2 6
showing how both numbers are multiplied by 2 (or whatever).
If there is time, your daughter might like to think up a way to do the same sort of thing, but starting with a fraction that is not in lowest terms, such as 4/6. One way is to color in 4 of 6 columns (probably best done with the paper in landscape position), then cut them all apart and rearrange them from 1 by 6 into a 2 by 3 formation, with the shaded pieces looking the way they do in my picture for 4/6. Proper use of tape can change the fraction to 2/3. The fact that both numerator and denominator can be evenly divided by 2 allows this to be done; you couldn't make such a rearrangement for 5/6, though you could for 3/6.
It’s actually possible to convert \(\frac{4}{6}\) to \(\frac{2}{3}\) more simply: just erase some lines:
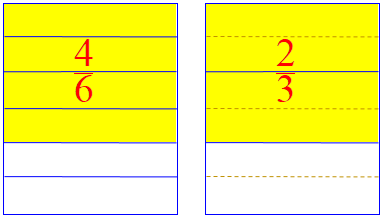
But that doesn’t make it fully clear that we are dividing each number by 2. What I had in mind was to make it look as much as possible like the earlier examples, where we just have one line to remove; the result would look like this after rearranging:
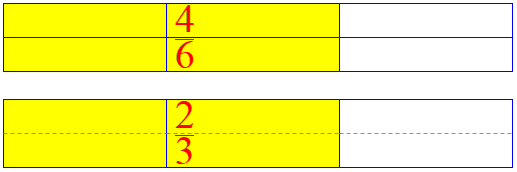
There's a lot to learn by playing like this!
