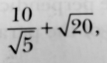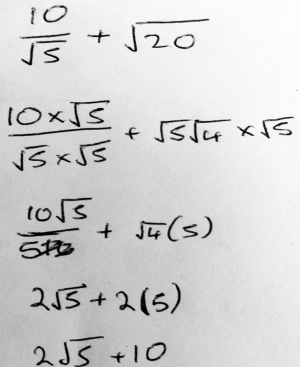(A new question of the week)
A recent question asked about the reasons for differences in the work of simplifying different kinds of radical expressions. We’ll look at that general question, with two specific examples, and then consider an older problem of the same type.
When do we need to use perfect squares and cubes?
The recent question is a long one, from mid-March:
So firstly, I apologize if my question is confusing. I wasn’t sure how to word it and that was the best I could do. Secondly, thanks for helping. So on to the question.
So this is about radicals and “perfect (squares, cubes, etc.)”
Let’s say we have 2 problems. The first one is this:
∛8 – ∛18
So this wasn’t too bad. 8 is a perfect cube and can be broken down to 2. This means that the answer to this problem is:
2 – ∛18
The second problem is this:
√120 ÷ √35
This is how I was shown how to do this:
√120 can be broken down to √10 and √12
√35 can be broken down to √7 and √5
This is now (√10×√12) ÷ (√7×√5)
These numbers can be broken down further:
√10 can be broken down into √5 and √2
√12 can be broken down into √4 and √3
√7 and √5 stay the same
I now have (√5 √2 √4 √3) ÷ (√7 √5)
The √5s on the top and on the bottom cancel out.
√4 reduces to 2
The √2 and the √3 can be multiplied to produce √6
So I now have 2√6 ÷ √7
I now rationalize both the top and the bottom to get rid of the √7 so I now have the answer:
2√42 ÷ 7
So my big question is this: why is it that in the first problem, ∛18 couldn’t be simplified?
I understand that there are no perfect cubes that go into ∛18, but in the second problem, that doesn’t seem to be an issue. √120 is reduced into (√10×√12). Neither √10 nor √20 are perfect squares, yet the problem was able to progress. Is there a rule regarding perfect squares/cubes/etc. that I am not aware of, where in some problems, it is important to look for these and in others, they hold little importance?
Why, in other words, is it correct to break √120 into √10 and √12, two non-perfect squares, vs it not being correct to break ∛18 into ∛6 and ∛3, two non-perfect cubes?
Thank you to anyone willing to answer my question. I know that it is long-winded, so I do truly appreciate it!
Summarizing his work, for the first problem he went directly to the conclusion and stopped,
$$\sqrt[3]{8}-\sqrt[3]{18} = 2-\sqrt[3]{18}$$
while for the second problem he factored the radicands almost completely, in several steps, then canceled,
$$\require{cancel}\frac{\sqrt{120}}{\sqrt{35}} = \frac{\sqrt{10}\sqrt{12}}{\sqrt{7}\sqrt{5}} = \frac{\sqrt{5}\sqrt{2}\sqrt{4}\sqrt{3}}{\sqrt{7}\sqrt{5}} =\\ \frac{\cancel{\sqrt{5}}\sqrt{2}\overset{2}{\cancel{\sqrt{4}}}\sqrt{3}}{\sqrt{7}\cancel{\sqrt{5}}} = \frac{2\sqrt{6}}{\sqrt{7}} = \frac{2\sqrt{6}\sqrt{7}}{\sqrt{7}\sqrt{7}} = \frac{2\sqrt{42}}{7}$$
Why, he asks, was he allowed, or even required, to use non-perfect-square factors in the second, while in the first, he only used perfect cubes? (He could have given an example with cube roots that involved more factoring, or one with square roots that used less.)
Sums and differences of radicals vs. product and quotients
I responded:
Hi, Jordan.
The main difference between the two problems is that a sum or difference of radicals can’t be combined (unless, after simplifying each term, they are like terms), while a product or quotient can be combined. It is the combination that allows you to do more, and that gives you a reason to do it.
In particular, the goal is to reduce each term to a single radical with as little as possible inside, and with no radicals in denominators (or denominators in radicals). The goal determines what you need to do; the “tools” (rules of radicals) determine what you can do. The former tells you what is useful; the latter tells you what is valid.
Jordan had obscured this distinction by using the word “correct”, which can be both too vague and too restrictive. Something can be “correct” in the sense of valid, without being the best way, or even helpful at all; and it can be “correct” in the sense of useful, without being the only way.
The first example is a difference:
In simplifying ∛8 – ∛18, all you can do is to simplify each term as much as it can be, which as you say leaves you with 2 – ∛18. Breaking the second radical up would accomplish nothing toward the goal.
Since the only way to simplify a sum is to combine like terms (in this case, like radicals), the initial goal is to create like radicals (if possible) by simplifying each term. Since 8 is a perfect cube, we can just take the root; then we can look at 18 and see that it has no perfect cube factors, so there is nothing to do. In effect, we are silently factoring it as \(18 = 2\cdot 3^2\) and seeing that the exponents are all less than 3 so there is nothing more to do. We could have written that bit of work if we wanted to, but we would just back it out anyway.
Let’s take a more interesting example of a sum, $$\sqrt{18}+\sqrt{50}-\sqrt{12}$$ Here we factor out perfect squares where possible: $$\sqrt{2\cdot 3^2}+\sqrt{2\cdot 5^2}-\sqrt{2^2\cdot 3}$$ Now we can take the roots of those squares: $$\sqrt{2}\sqrt{3^2}+\sqrt{2}\sqrt{5^2}-\sqrt{2^2}\sqrt{3} = 3\sqrt{2}+5\sqrt{2}-2\sqrt{3}$$ Finally, we combine the first two, which have the same radical: $$8\sqrt{2}-2\sqrt{3}$$ At each step, we used perfect squares; if in any case we couldn’t find one, we would leave that term untouched.
On the other hand, in complicated cases, we might need to explore to find those perfect squares, and therefore might write factorizations that are not yet at the goal. For example, to simplify \(\sqrt{10,800}\), we might do this: $$ \sqrt{10,800} = \sqrt{108\cdot 100} = \sqrt{2\cdot 2\cdot 27\cdot 10^2} =\\ \sqrt{2^2\cdot 3^2\cdot 3\cdot 10^2} = 2\cdot 3\cdot 10\sqrt{3} = 60\sqrt{3}$$ At various points we had factors that were not perfect squares; but the goal was to find perfect squares hidden among them.
The second example is a quotient:
In simplifying √120 ÷ √35, you need to combine the radicals into one. My own usual procedure is to do that first, rather than after first breaking things apart as you did. I combine them to get √(120/35), and simplify the fraction to get √(24/7). My new goal is to get the 7 out of the radical, so I pull it back apart as √24/√7, and then simplify the numerator to get 2√6/√7. Finally, I rationalize the denominator by multiplying by √7/√7 to get 2√42/7. The result is the same as yours, but I think this approach makes the reason for each step clearer. At no point did I split a radical into two parts, neither of which was a perfect square.
Here is the work by my preferred method: $$\frac{\sqrt{120}}{\sqrt{35}} = \sqrt{\frac{120}{35}} = \sqrt{\frac{24\cdot 5}{7\cdot 5}} = \sqrt{\frac{24}{7}} = \frac{\sqrt{24}}{\sqrt{7}} =\\ \frac{\sqrt{4\cdot 6}}{\sqrt{7}} = \frac{2\sqrt{6}}{\sqrt{7}} = \frac{2\sqrt{6}\sqrt{7}}{\sqrt{7}\sqrt{7}} = \frac{2\sqrt{42}}{7}$$
If I didn’t combine into a single radical first, I would simplify each radical by itself (working with larger numbers) and then simplify the fraction: $$\frac{\sqrt{120}}{\sqrt{35}} = \frac{\sqrt{4\cdot 30}}{\sqrt{35}} = \frac{2\sqrt{30}}{\sqrt{35}} = \frac{2\sqrt{6\cdot 5}}{\sqrt{7\cdot 5}} =\\ \frac{2\sqrt{6}\sqrt{5}}{\sqrt{7}\sqrt{5}} = \frac{2\sqrt{6}}{\sqrt{7}} = \frac{2\sqrt{6}\sqrt{7}}{\sqrt{7}\sqrt{7}} = \frac{2\sqrt{42}}{7}$$ Here it was less obvious that we had to factor out the \(\sqrt{5}\). But I still did less random factoring than Jordan did.
Why not factor more or less than he did?
Now for your question.
The reason we don’t break up ∛18 into ∛6 ∛3 (or ∛18 into ∛9 ∛2) is that it doesn’t move toward the goal, which is a single small radical; a product of two radicals is not considered simple.
The reason we do break up √120 and √35 is that some of the resulting parts will cancel.
Again, doing it my preferred way, the cancelation was more natural, and didn’t involve pulling a non-perfect square out of a radical:
In my method, I didn’t break up a radical until there was a visible reason to do so, namely having a radical that would be in the final answer, that can be reduced. (If the radical in the denominator could be reduced, I could either reduce it right there, to make the final rationalization simpler, or rationalize as is and then reduce the radical that ended up in the numerator.)
As an example for this last comment, if I had to simplify \(\displaystyle\frac{\sqrt{5}}{\sqrt{63}}\), I could either simplify the denominator first and then rationalize, $$\frac{\sqrt{5}}{\sqrt{63}} = \frac{\sqrt{5}}{\sqrt{9\cdot 7}} = \frac{\sqrt{5}}{3\sqrt{7}} = \frac{\sqrt{5}\sqrt{7}}{3\sqrt{7}\sqrt{7}} = \frac{\sqrt{35}}{21}$$ or rationalize the denominator first, and then simplify radicals: $$\frac{\sqrt{5}}{\sqrt{63}} = \frac{\sqrt{5}\sqrt{63}}{\sqrt{63}\sqrt{63}} = \frac{\sqrt{5}\sqrt{9\cdot 7}}{63} = \frac{3\sqrt{5}\sqrt{7}}{63} = \frac{3\sqrt{35}}{3\cdot 21} = \frac{\sqrt{35}}{21}$$
In your work, you eventually split up every radical into a product of primes and powers of primes, much as one can factor a fraction into powers of primes, in order to find factors that cancel. That is a valid approach, though perhaps more work than was necessary. You ended up putting some of them back together, just as you would have to do with your cube root if you split it up.
In the latter case, we know not to do it because there would be nothing to do with the parts other than undoing what you just did. In the former case, you split it up in the hope that it would be useful, and it turned out to be so. In my approach, I split up only what I knew would be useful.
Sound good?
Of course, I was mentally splitting things up further, but recognizing which I didn’t have to write.
A general rule in algebra is to do only what you are allowed to do (following properties of radicals, etc.) and to do whatever will be useful. If something isn’t legal, you can’t do it; if it is not useful, you may be wasting effort, but it is not actually wrong.
Again, you can do all sorts of things in algebra that are not ideal, but you can’t do anything that isn’t legal. I happen to have just run across a similar statement in one of the earliest posts in our blog:
There I said, “genuine understanding … not only helps us to do the right thing, but also frees us from slavery to mere “rules”, opening our eyes to see alternatives and know that they are legal, even though they are not usual.”
Jordan replied,
This is an amazing reply! Thank you very much, Doctor Peterson! Have a good day.
To which I said,
Thanks for the question! I love when students want to understand, and tell me how they are thinking; it inspires me to think in different ways, which is a lot of fun.
Another example
I looked for another question that would further illustrate this sort of work, and found this from July, 2019:
Hi
I have to simplify this square root fraction: 10/√5 + √20The answer is 4√5, but I do not get to that answer. Please help.
When I tried it I got to the answer 2√5 +10.
My steps were 10*√5 / 5*√5 + √4√5*√5,
then I got 10√5/5 + 2*5.
Lastly I simplify to get 2√5 + 10.
This involves both a division and an addition. Doctor Fenton answered, pointing out a potential ambiguity in the way an expression is written, and asking for the reasoning behind two steps that don’t make sense as he did them:
Hi Mooija,
I don’t understand how you are attempting to simplify the expression. You change 10/√5 to 10*√5 / 5*√5.
Is the right side of this equation
10*√5 10*√5 ------- or ------- * √5 ? 5*√5 5That is, you have rewritten an expression in the form a/√b in the form
a*√b / b*√b .Can you explain why you are doing that?
You also change the second term √20 to √4√5 * √5 . That is, you have changed an expression of the form √(a*b) to √a * √b *√b. Can you explain why you are doing that? I don’t understand your reasoning behind these operations.
Mooija answered, clarifying what he had written, by using images of the problem and of his work:
Okay I think this might make it easier
The first one is a picture of the expression straight from my book.
The second is the way I solved it (that is still wrong).
We can see that the error in the first term was just a typo, but the second term has an actual error.
Doctor Fenton replied,
Thank you. That explains a lot.
In both terms, as I explained earlier, you are multiplying the given expression by an expression which is not equal to 1. That is similar to taking 2 + 3 and multiplying the first term by 4 and the second term by 2, getting 2*4 + 3*2 = 13, which is not the same as the original expression (whose value is 5).
In the image, Mooija has multiplied the first term by 1, in the form \(\frac{\sqrt{5}}{\sqrt{5}}\), but the second term by \(\sqrt{5}\).
To combine two radical expressions, you need to have both in the same form. Your expression 10/√5 has the surd in the denominator, and the second term √20 has a different base (20 instead of 5). The second term, √20, can be simplified by using the property of square roots that √(a*b) = √a * √b. You did that in writing √20 = √4*√5. Now both terms contain the surd √5, and √4 can be simplified to 2, so √20 = 2√5. Now your expression has become 10/√5 + 2√5. However, while both terms have the same surd, in the first term, the surd is in the denominator.
Here, we’ve simplified only the second term so far. As for the first term, Mooija had obtained the right answer the first time but miswrote a step; Doctor Fenton reminded him of the correct procedure:
What you want to do is to change the FORM of a number, without changing its VALUE. (Dividing 10√5 by 5√5 changes the value. The only way to change the form without changing the value is to multiply or divide by 1. You need to find a way to write the number 1 in a more useful form for this problem.) Can you think of a way to write 1 so that multiplying 10√5 by 1 in this different form will become a number with no surd in the denominator?
This is what Mooija showed in the image: $$\frac{10}{\sqrt{5}} = \frac{10\sqrt{5}}{\sqrt{5}\sqrt{5}} = \frac{10\sqrt{5}}{5} = 2\sqrt{5}$$
What you have written on the images you just supplied is not what you wrote originally. In your original question, you wrote
my steps were 10*√5 / 5*√5 + √4√5*√5
then i got 10√5/5 + 2*5
That first term is
10*√5 10√5 ------- , not ------- 5*√5 √5 * √5as you write in the attached images for this reply. That correctly simplifies to 2√5. But in your second term, you have written √20 = √4 √5 * √5 which you wrote as √4*5. But √20 = √4 * √5=2√5 .
Multiplying by the additional factor of √5 changes the value and is not correct.
Do you see why 4√5 is the correct answer?
Mooija confirmed it:
Yes I understand what I did wrong now.
Thank you very much
The correct work is: $$\frac{10}{\sqrt{5}}+\sqrt{20} = \frac{10\sqrt{5}}{\sqrt{5}\sqrt{5}}+\sqrt{4\cdot 5} = \frac{10\sqrt{5}}{5}+2\sqrt{5} = 2\sqrt{5}+2\sqrt{5} = 4\sqrt{5}$$