(New Question of the Week)
An interesting trigonometry problem came through about a month ago, answered by Doctor Rick. It gives a nice example of how our process works at its best. It is also an interesting problem!
The problem
Here is the question, from John:
The question: The square PQRS has points A and B within its area such that PA, RB and AB are of equal length. Lines PA and RB are parallel. What is the lowest possible value for angle SPA?
My thoughts so far: So far I’ve come up with two possible routes to a solution. The first involves creating some expressions for certain values within the question involving trig, and then creating and solving a trig inequality. The second involves creating a polynomial equation where y = angle SPA, and then performing optimisation to find the lowest value. The second option seems (to me at least) to be more promising. The only progress that I have made, however, is forming some basic trig expressions for a few lengths. I don’t think that I have anything which is actually useful.
Here’s what I have so far, anyway:
Imagine that point E is on line PS so that triangle PAE is right-angled at E. In the triangle PAE, where C = hypotenuse, A = adjacent, and B = opposite (relative to angle SPA):
cosθ = A/C
A = Ccosθsinθ = B/C
B = Csinθ(Ccosθ)2 + (Csinθ)2 = C2
I’m struggling to use any of this to actually find an answer, however. The issue is that I can’t find a way to incorporate line PQ into any of my equations.
I drew a couple of diagrams, thinking in terms of line PA rotating about P and line RB rotating about R. The angles that these lines make with their respective vertical side of the square are alternate interior angles, so angle SPA must be congruent with angle QRB.
In this view, you’ve got two circular arcs (same radius) inside PQRS. Point A is on the arc in the upper left of the square, and point B is on the arc in the bottom right. The distance AB must be the same as the radii.
I’m just not sure which line of working to follow, as I’ve tried them all to no avail. Ideally, I’d like someone to give me an idea of what to do, and essentially to put me on the right track towards figuring it out.
John helpfully described the problem and his thinking in full; though he is right that not much of this is useful as a solution, it definitely helps us see where he stands! Here is a picture of what he has described (though I can’t yet be sure where he placed P, Q, R, and S, and therefore what he means by upper left):
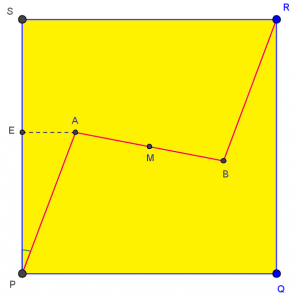
Help with the problem
Doctor Rick replied with a first idea for looking at the problem, and a summary of his own method of solution (which implicitly tells John that it is solvable, and makes it clear that the goal is to get John to find his own solution):
Hi, John.
One thing might help to simplify things, whatever approach you use. Have you noticed that points A and B are symmetrical with respect to the center of the square? Thus the midpoint of AB is at the center of the square.
I was able to solve the problem by first writing an equation in cos(SPR) using the Law of Cosines on a particular triangle. Then I used calculus to minimize that cosine (which thus maximizes angle SPR and minimizes angle SPA). Calculus might not be in your “toolbox” yet, but you did mention optimizing so perhaps it is.
Note that we often have to make guesses as to what a “patient” knows (his “toolbox”), even when he has told us a lot; here, we don’t yet know that John knows calculus, but it seems likely. John confirmed this:
Hi again,
Yes, I have done some optimisation work, and I have also done differentiation and integration involving trig. I haven’t specifically done trig optimisation yet, however I’m sure that it’s just the same as regular optimisation. I’m in the UK (hence the spelling of optimiSation), where it’s getting a bit late, so I’ll take a look at this tomorrow and let you know how it goes. What you’ve said does make sense, and I look forward to hopefully solving the problem. Thanks,
John
Doctor Rick added another simplifying hint for overnight pondering (at this point, if you’re wondering, 4 hours have elapsed, and they are 5 times zones apart):
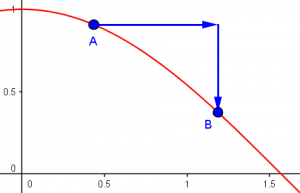
Hi, John. Just a hint for when you get back to this problem tomorrow … You don’t really need to do trig optimisation. (See, I can speak English. 😉 ) As I suggested, you can just optimize cos θ — that is, let cos θ = y and optimize y. Since y = cos(x) is a decreasing function of x, when y is minimum, x will be maximum, and vice versa.
This is an important idea that beginning calculus students often miss: When you want to optimize a complicated function, you do not have to do directly what you are asked to do, but can find a simpler function with equivalent behavior. A typical use of this strategy is to maximize or minimize the square of a distance instead of the distance itself; here, it is to maximize the cosine rather than minimize the angle (which would have required working with an inverse cosine, which is much more complicated). We can do this because the cosine is a monotonically decreasing function; that is, when θ gets larger, cos θ gets smaller, so the largest value of θ (as long as it is acute) corresponds to the smallest value of cos θ:
Then, 22 hours later, John wrote back, showing that he had been thinking, but needed a little more:
Hi again,
I’ve been looking more closely at what you’ve said with regards to: “writing an equation in cos(SPR) using the Law of Cosines on a particular triangle,” and I’m not entirely sure what you mean. I’ve attached an image of how I’m imagining the problem, and in that diagram angle SPR is always 45 degrees (as SPQR is a square.) I’d appreciate it if you could clarify what you meant by that. Thanks,
John
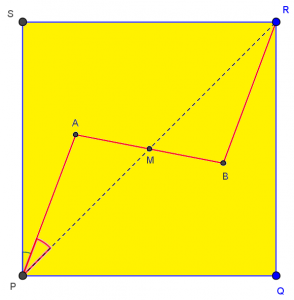
His attachment was a sketch of the same basic picture (which showed us how he oriented it).
Yes, “SPR” was a mistake; and showing the picture leads to a new hint:
Sorry, angle SPR was a typo. You’re right, that angle is fixed at 45 degrees. What I meant to say was that maximizing angle APR (not SPR) will minimize angle SPA, since SPA + APR = SPR = 45 deg.
In your figure, how about adding point M, the midpoint of AB? That’s what I was hinting would be useful — and then you can consider triangle APM.
Note how we are transforming the problem from minimizing SPA, to maximizing APR, to minimizing cos(APR). Here’s the picture as we have it so far:
Another 14 hours, and John reported victory (without having to show any work):
Hi again,
I think that I’ve reached the correct answer. I did as you suggested, and found the minimum value of angle SPA to be 15 degrees. Thanks again for all your help so far. I’d really appreciate it if you could confirm that this is also the answer that you reached.
John
That’s how our mentoring is supposed to work; we give enough help to enable a student, but not enough to disable him. And then we can affirm his success:
Yes, I too found that the minimum measure of angle SPA is 15 degrees. I found the answer using the method I suggested; I also confirmed it (approximately) using geometry software GeoGebra.
The solution …
I had been using the same software as I watched this interaction; here is my version, showing the manually located minimum:
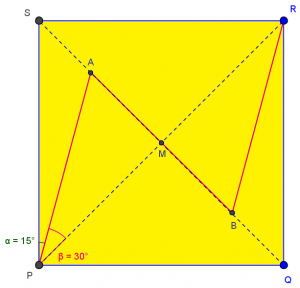
Interesting, isn’t it? Since it didn’t come out in the discussion, let’s carry out Doctor Rick’s work:
Consider triangle APM, and take AM to be 1 unit for simplicity. If \(AM = x\), then \(AP = 2x\). Applying the Law of Cosines with angle P, we have \(x^2 = a^2 + (2x)^2 – 2(2x)\cos(P)\), and solving for \(\cos(P)\) yields \(\displaystyle\cos(P) = \frac{3x^2 + 1}{4x}\). Differentiating and setting the derivative to zero, we find that \(\displaystyle x = \frac{1}{\sqrt{3}}\), so that \(\displaystyle\cos(P) = \frac{\sqrt{3}}{2}\) and P = 30° and angle SPA is 15°.
… and more questions!
The nice answer, involving equilateral triangles, certainly suggests that there might be a simple geometrical proof; any ideas? Here’s a hint, thanks to GeoGebra’s locus feature: point A is always on the semicircle (actually, the whole circle) that I have added here:
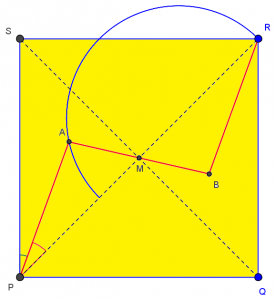
This will remind anyone whose has studied conic sections as loci of various interesting facts; and once you prove the locus, the maximization of the angle is “obvious”. But I will stop here. Enjoy!
