How Can I Remember Area Formulas?

Students often ask about formulas for areas or volumes. Sometimes they are just overwhelmed by the number of formulas they need to know; other times they are curious about how we know they are true. The answer to both questions is, in part, the same: if you know at least something of where they come from, you can either memorize them more easily, or just derive them when you need them.

Dr. Ian emphasized here that we shouldn’t rely on memory for most formulas:

Math for a Future in the Sciences

I've had a hard time with math for the last three years. The theorems, equations, patterns etc. all seem to pile up - it's impossible to memorize them all. Or sometimes I won't understand a concept... . Is there anything you can recommend for someone who wants to learn math on his own, and be able to retain information for the years to come?

Part of his answer:

I can sympathize with you, because I have a similar problem. I've _never_ been able to remember formulas, and the way that I've had to compensate is that whenever I learn a new formula, I have to learn how to derive it from first principles - by which I mean, the things that are so basic that I _can't_ forget them. (One of the luckiest breaks I ever caught in my life was when I took second-semester calculus in college.  That's the semester when you have to memorize about a zillion formulas that all look pretty much the same - one plus or minus the sine or cosine of plus or minus something, under or over the square root of something similar - so I fully expected to fail. But on the first day, the professor said: "I don't expect you to remember anything that I can't remember, and the only thing that I can remember is that cos^2 + sin^2 equals 1." So you're not alone!)

(I say something very similar to my classes all the time.) He goes on to make several suggestions for memorizing formulas in general, and closes with this:

In the end, you may find that your memory just isn't going to work as well as you want it to, in which case... there's always paper and ink! That's what they're for, really, so don't be ashamed to make use of them. If you have to choose between remembering things you don't understand, and understanding things that you can't remember, I strongly recommend the latter.  :^D

Here is another discussion, specifically about area formulas, which is my main topic here:

Remembering Area Formulas

Hi, I was wondering if there was a good way to help me memorize the formulas for areas of different shapes. I am having a lot of trouble doing that and I need help. Is there a funny saying, or something?

Dr. Ian again gave some good advice on memorization, starting with the fact that pure memorization is not a good idea:

You only need to memorize things that you don't understand, so feeling like you need to memorize something is a sign that you still don't understand it.  

And when you memorize things, it's easy to recall them incorrectly, by dropping a minus sign, or mixing up the numerator and denominator, or in a hundred other ways.

He gives references to places where we had provided the necessary understanding of non-geometric topics, and concludes:

Understanding examples like these is kind of like keeping a spare key hidden under the ceramic frog next to your back door... you can use it to let yourself in if you ever lock yourself out of the house. 

If you'd like to write to me and tell me about some things that you're trying to memorize, I can try to help you understand them in a way that will make memorization unnecessary.  Would you like to try that?

Then Dr. Achilles goes through some specific examples, showing how the basic area formulas can be learned in terms of their derivation:

First there are two things you have to memorize. Only two, though! 1) The area of a rectangle is width * length. 2) The area of a circle is pi * radius * radius. Then, when you see any other area problem, just use those two facts to figure out the area. A square is easy enough to figure out. A square is just a special type of rectangle in which width = length.  So you just multiply side * side and you've got it.

He uses pictures to make each of the basic formulas “obvious”. Here are my versions of them:

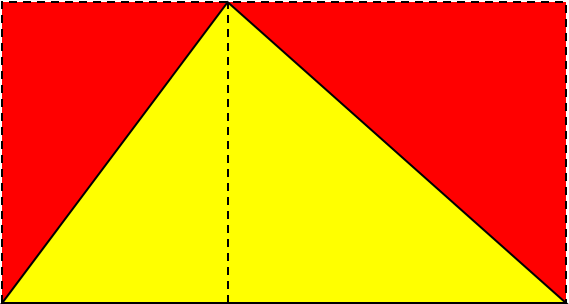
For a triangle, enclose it in a rectangle with the same base and height, and draw an altitude to the base; the red triangle on the left is congruent to the yellow triangle, and likewise on the right; so the red area is equal to the yellow area, which is half of the rectangle. So the area of a triangle is half the area of the rectangle with the same base and height: \(A = \frac{1}{2} bh\).

For a parallelogram, draw the rectangle with the same base and height. You can see that if you cut the yellow triangle off from the right side of the parallelogram and move it to the right, you get the rectangle; so the areas of the two figures are the same: \(A = bh\).

For a trapezoid, draw a rectangle whose top and bottom lie on the same lines as for the trapezoid, but whose left and right sides pass through the  midpoints of the sides of the trapezoid. Again, if you cut the yellow triangles off the bottom corners and put them on the top corners, you have made the rectangle; so the areas are the same. The area of the trapezoid is the same as the area of a rectangle with the same height, and base equal to the average of the bases of the trapezoid: \(A = \frac{B+b}{2} h\).

(These are not full proofs; if a base angle of the triangle or trapezoid were obtuse, or if a corner of the parallelogram did not lie above the base, then these constructions would not work. But our purpose here is just to remind ourselves of the formulas, not to satisfy a mathematician.)

Dr. Achilles concluded with words similar to Dr. Ian’s:

Plus, if you learn the reasons why areas equal what they do, instead of learning a funny rhyme, then if you ever forget the formulas completely, you can always figure them out again; but if you ever forgot the rhyme, you'd be stuck with nowhere to go. Learning math takes a lot of practice, but if you try to learn why things are the way they are, instead of just memorizing formulas with no reason behind them, you'll do better and you'll enjoy it more.

By the way, there are some “funny sayings” that you may find helpful; for example, for the area of a circle, you can remind yourself that “pie are not square – they’re round”  (\(A = \pi r^2\)). That happens to be one of the formulas Dr. Achilles said to memorize – though one of these days I’ll show you some ways to understand the areas of the rectangle and the circle, too – along with ways to tell whether the formula you remember is for an area or something else.

Similar derivations can be found here (by Dr. Jeremiah and Dr. Rick, respectively):

Figuring Out Formulas for Area

Finding the Area of Squares and Triangles

The latter gives a different way to handle the trapezoid, as does

Formula for the Area of a Trapezoid

One student asked about something a little different: is there a single formula that applies to every figure? Dr. Ian worked that out (though of course it doesn’t really cover everything – just the cases we’ve been looking at here:

General Area Formula

I heard that there was an all-inclusive formula for the area of a square, rectangle, parallelogram, trapezoid, and triangle.  Is this true?  I have looked everywhere, but I can't find anything.

The answer is that the all these figures can be thought of as trapezoids, because they all have parallel bases – if you are willing to think of the “top base” of a triangle as a single point with length zero. So you can always multiply the height by the average width (the average of the top and the bottom) to get the area!

Finally, let me refer you to this page, which does the same sort of thing for three dimensional figures:

Helpful Ways to Remember Cylinder and Prism Formulas