(New Question of the Week)
Last month we had a question from a Czech student asking about a geometry problem. The discussion illustrates language issues that can arise, and how we try to guide a student to solve a problem himself. I will fill in some gaps as we examine how to approach an interesting problem.
Finding what the problem means
Here is Adam’s question:
Hello,
I need help solving a math problem, a good friend asked me for help, but I wasn’t able to solve it and now I am asking you for help.
The problem:
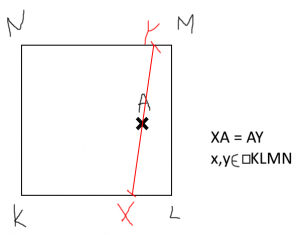
You have a Square K,L,M,N and a point A, that lies inside of the square. Find all lines, named x, y, for which A is the center and the circumference of the square is their edge.
I hope you understand me, my English is really not that good, here is a drawing I made for it to be a bit clearer. The black is given but can be chosen freely (except the centre, which would give an infinite amount of results and on the parallels, those are obvious), the red would be the result, but it has to be proven
Several details were unclear, so Doctor Rick asked for clarification, restating the problem as he understood it, and asking what kind of answer is needed (which is something people often omit, because it is obvious to them, knowing the context of the problem):
Hi, Adam.
I am not sure I understand every detail of what you’ve said. I understand it to be this: Given a square ABCD and an arbitrary point A inside the square, identify all pairs of points X, Y on the perimeter of the square such that |AX| = |AY|. What isn’t clear is how you want the points X and Y to be specified.
We could, for instance, use coordinate geometry. Let the vertices of the square be K (0, 0), L (s, 0), M (s, s), and N (0, s) where s is the side of the square; and let A be (a, b). Then we can give the coordinates of X and Y in terms of s, a, and b. Is that the sort of thing you have in mind? If not, can you say what you would consider an appropriate way to give a solution to the problem?
I understand that if A is at the center, then for any point X on the perimeter of the square, choosing Y at the opposite point on the square will fulfill the conditions. I’m not sure what you mean by “on the parallels”. If you mean on either of the lines through the center and parallel to a side of the square, that description fits the point A in your figure; I consider this to be “obvious”, but it might not be what you’re thinking about. Maybe you mean the diagonals KM and LN; in that case there is one solution and it’s reasonably obvious.
Let me know what you have in mind, and we can work together. I also want to know something about why your friend wants to solve this, and how you and he/she have tried to solve it.
Adam clarified, showing that the context is pure geometry, not analytic geometry:
Thank you for your answer, the problem has to be solved geometrically, by drawing. Yes, the ones that you said are obvious, what is problematic is finding the solution when A is placed in a random place.
My friend needs this problem solved for homework, she asked her classmates and me, because she wasn’t able to find out how to solve it, but no one she asked yet was. I attempted many things, even brute forcing it through trial and error, but I am unable to find a logical solution to it.
Exploring the problem
Now we could move forward; but in order to give help rather than an answer, it is necessary to have some idea of what knowledge the student has that could be used to discover a solution:
OK, I understand now that you’re looking for a geometric construction of points X and Y. That helps a lot!
What you haven’t told me yet is what your friend has learned in class that might be useful. I see a very easy construction — in fact, I’d say extremely easy (one step). It might be seen in several ways. For instance, you might use some knowledge of circles, or of right triangles, or maybe just congruent triangles.
Your figure may be misleading you, because it applies to one of the special cases I mentioned. If I were you, I’d start with a figure in which A is closer to one vertex of the square (say, M) than to the others.
Do you realize how I know that A in your figure is on the line through the center and parallel to KL? In case you don’t, it’s because you put X and Y on opposite sides of the square. So in your new figure, don’t do that!
There is a very important point here, related to what I have said previously about the role of diagrams in geometric proofs. When the diagram one is looking at represents a special case, one sees things that are not relevant to the general case one wants to solve; so we want to avoid special cases. This is why, for example, I draw a scalene triangle when experimenting with a problem about triangles, to avoid seeing things that only apply to isosceles triangles.
The figure Adam supplied shows X and Y on opposite sides of the square, which forces the midpoint of XY to lie on a parallel line through the center, the very case Adam has already solved and is not asking about. This tells us that X and Y in the general case will always lie on adjacent sides. If I were drawing a figure, I would probably work backward (as suggested in the earlier post), first putting X and Y on adjacent sides, then finding the midpoint M. The resulting figure (you will see Doctor Rick’s version soon) represents the state of things after the problem has been solved, when an arbitrary point M had been chosen. I would then look for relationships that could be used to construct M if it were not already there.
Adam responded with an appropriate figure, but without drawing XY as I just suggested, and without making any real progress:
Ok, see the attachment for the example, no matter what I should or should not know, what is the simplest way of finding the geometric construction for X and Y? I know how to find them if A lies on the diameters [diagonals] or parallels, that is simple, but not when it is randomly placed. Maybe I am just missing something obvious though.
Here is the point at which it can be hard to help: He is acting a little impatient, asking for “the easiest way” to find the solution; but we still don’t know what he or his friend knows that could be of use – what solution they will most easily find given their background. Any hint we give will be pushing them along a path that might not be natural to them, and not helping them learn how to find solutions without help.
With hindsight, I might have suggested drawing the figure in reverse as I said above, which doesn’t give much of a shove in any particular direction; Doctor Rick went one step beyond that, showing that figure with an additional line that reveals a powerful idea:
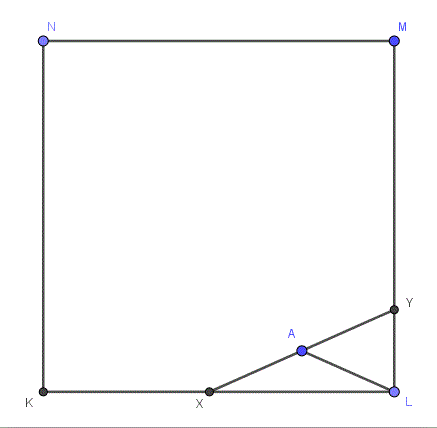
Hi, Adam. Yes, what you’re missing is fairly obvious, once you see it. 🙂 Maybe the attached figure will be sufficient.
He chose X and Y arbitrarily (using Geogebra, which is an excellent tool for experimenting with geometric figures), constructed the midpoint A, and then drew in AL to the nearest vertex of the square. This reveals two (provably) isosceles triangles, showing that X and Y are the same distance from A as L, and leading to the simple construction Doctor Rick mentioned at the start … if you see it!
Discovering the construction
Oh, so the line |LA| works as the arms for two isosceles triangles?
And there can be even two results, right, if the point A is closer to the center then there can be a line going from L through A, and further through the square?
Adam saw the immediate implication, but didn’t mention how to construct it.
Doctor Rick responded:
Yes, AX = AY = AL. Do you see the one step needed for the construction?
I don’t see what you’re thinking in regard to “a line going from L through A and further through the square.” How would that line (LA extended) relate to an alternate pair of points X and Y?
I don’t have a formal proof that there is only one solution when A is not on what you call the “parallels,” but I’ve pretty well convinced myself of that informally. There is plenty more to talk about in relation to this problem, so feel free.
Adam wanted to move on:
Yeah, my bad, you are right, it would have to lie in the middle of the square for that to be correct.
If you have time, there is a similar problem, it would be best if you hint the way like last time, even though you pretty much solved it for me, for which I am very grateful 🙂 …
But there was more for Doctor Rick to say:
Hi, Adam. You’re right, in the end I practically gave it away, and I would prefer that you do more of the thinking. If you’re satisfied with the state in which we left that problem, OK, but as I said, there is more that both of us could think about! For one thing, you didn’t answer my question about the one step needed to do the construction. That isn’t hard at all, so I hope you just didn’t bother to say it.
Adam still didn’t quite state what the construction was:
Yes, I see the construction step, by connecting the point A to the nearest apex, you find the length of AX and AY, because it creates a double triangle sort of construction, I am not sure how I would be able to solve the problem without prior knowledge of such a property though.
Doctor Rick finally stated the answer directly:
I don’t think you do see the construction step. It is to draw a circle with center A, passing through L (or whichever vertex of the square is closest to A); the intersections of this circle with the adjacent sides of the square are X and Y. Perhaps you are not familiar with classical construction, or perhaps that is not really the form of solution you need.
It is not clear to me what you mean by “without prior knowledge of such a property.” Are you saying simply that you wouldn’t have thought of this construction on your own? That’s why I should have given you less in the way of hints, so you’d have to exercise your mind more — that’s what homework is for.
But in fact Adam had seen the construction:
Oh yeah, I did that in my construction, I just didn’t realise that is what you were asking haha, I explained to my friend, that she has to use a compass, put the point in A and draw a circle from L around, the points of conflict being the x and y, sorry for the confusion.
Drawing the circle is a beautifully simple answer; this is a very nice problem for demonstrating how to think creatively and find a way to do something that is not at all obvious at first.
(Now, the problem required finding all such lines, including the special cases, and also requires proof; so Adam is not finished. But we have good reason to believe he can handle the rest.)
After this, they were off looking at another interestingly simple problem, which I don’t have room for here …