Here is a recent question about arithmetic sequences and series (specifically, reversing the process to find the number of terms given the sum), that nicely illustrates a common type of interaction with a student: gathering information about both problem and student, then guiding them to use what they know, or giving new information as needed. We’ll see how formulas can be used in solving problems, but are not all we need.
When will the sum reach 200,000?
At the very end of March, Daniel wrote to us with this question:
I currently have 3260 units of inventory/stock. Each month the stock purchased increases by 10 units (so next month will be 3270 and the month after, 3280). Assuming no stock is sold, stolen or destroyed, how many months will it take to reach 200,000 and how many units of stock would have been purchased in that final month?
Please include formula, thank you in advance.
Sometimes we get real life problems that can look a lot like word problems; but Daniel gave his age as high school, and the situation is a little too precise for real life! So we can infer the general context, but not Daniel’s level of knowledge, or what he has been learning that he is expected to use. So we need to start by finding out about those things.
What formulas do you know?
Doctor Rick answered, giving a hint while asking for information:
Hi, Daniel, thanks for writing to the Math Doctors.
This problem is about arithmetic series. Rather than provide you with a formula (reinforcing the wrong idea that math is all about formulas), I want to know what you have learned recently, so that I can help you apply what you already know.
What are your thoughts about the problem? When I say “arithmetic series”, that’s a big hint assuming you have learned about them — and I imagine the problem comes from a unit on arithmetic series. Have you learned any formulas or done example problems? That could be a starting point for thinking about your problem. Please show me what you can do, even if that is only to list possibly relevant definitions or formulas.
If the name “arithmetic series” means nothing, then what have you been learning? There might be another way to approach the problem.
It is quite common for people in or out of school to expect that a formula will solve every problem; but most problems require a mix of formulas and thinking about how to use them. Formulas are tools in our toolbox; problem-solving ability involves choosing the right tool for each step of a project.
First attempt
Daniel replied, providing just what we need to make a start at helping: his state of knowledge, and a first attempt.
Hi Doctor Rick,
Thank you for your response.
I apologise for not showing my workings.
I am aware of 2 formulas which I understand:
- an = a1 + (n – 1)d
- sn = (n/2)(a1 + an)
I have attached a page showing my workings but it is here where I also hit a wall.
In summary, while I suppose that I can keep randomly guessing “n” until I chance upon the correct number, this method is only feasible for homework because during tests and exams, I won’t have the luxury of time on my side to muddle through it randomly.
I’m fairly certain that a formula does exist for this but I can’t seem to figure it out on my own.
Thank you again for your assistance.
Kind Regards
He has made a good start. He identified the two formulas (one for the nth term of an arithmetic sequence, and one for the sum of n terms). He sees that the first term (the first amount purchased) is 3260, and the common difference (the increase from any term to the next) is 10. For practice, he applied the first formula to find the amount of the 20th purchase; this amounts to the fact that the first was 3260, and it has been increased by 10, 19 times, for a total of \(3260+19(10) = 3450\).
Then, the total amount purchased in these first 20 months is given by the second formula, which in effect multiplies the average of the first and last terms by the number of terms: \(\frac{20}{2}(3260+3450)=67,100\).
But if this is just the beginning of a trial-and-error search for the value of n needed to reach a total of 200,000, it will take some time. We might, for example, guess that since the goal is more than twice the amount at 20 weeks, maybe we should try \(n=40\). Then we get $$a_{40}=3260+10(40-1)=3650\\S_{40}=\frac{40}{2}(3260+3650)=138,200$$
That isn’t enough, so we’d keep trying. It wouldn’t take too much longer if we make good guesses (not too cautious, and not too wild); but surely there is a more direct way?
Making an equation
Doctor Rick responded, suggesting the next “tool” that will be needed, which hopefully Daniel is aware of from other lessons, and didn’t realize it could be used here:
Thanks for the work. Now I can see what you know and where you are having trouble, so I’m in a much better position to help you!
There is another formula you will probably be using, but it’s not a formula specific to this kind of problem; it’s the quadratic formula.
The idea is to use both the formulas you showed to write an equation that says the sum of the first “n” terms of the series is (at least) 200 000. Then, instead of guess-and-check, you just solve the equation for n.
Here’s a start. You’ve got the equation
Sn = (n/2)(a1 + an)
and an equation for an:
an = a1 + (n – 1)d
Use the second equation replace an in the first equation, and replace Sn, a1, and d with values given by the problem. Then you’ll have the equation in n. Give this a try.
This is a key idea of algebra: When you need to find out what value of a variable will make some condition true, you express the condition as an equation and solve for the variable. We want to find the value of \(n\) for which \(S_n = 200,000\), so we need to express \(S_n\) as an expression in \(n\), set that equal to 200,000, and solve.
Daniel answered,
Thank you for your response Doctor Rick,
I looked up the quadratic formula and the slew of alphabets and roots has completely baffled me.
Looking at the second part, I tried to follow your instructions as per the following
an = a1 + (n – 1)d
Sn = a1 + (n – 1)d
200,000 = 3260 + (n – 1)10
200,000 -3260 = 10n – 10
196,740 – 10 = 10n
196,730 = 10n
19,673 = n
Somehow it looks as though I’ve made things worse…
I’m not looking to be spoon-fed by any means and I apologise if I’m coming across that way, but it I am finding it slightly difficult to understand.
Please can you show me where I’ve gone wrong?
Kind Regards
So he clearly has never seen the quadratic formula, and perhaps is not even ready to learn it; this strongly suggests that he is expected either to solve the quadratic equation we’ll be writing using another method (such as factoring, if possible), or else just to use trial and error (“guess and check”) as he started to do.
We’ll get back to that; but for now we can look at his work, which since it didn’t result in a quadratic equation, contains an error somewhere. And we see it quickly: On the second line of work, he used the formula for the nth term as if it gave the nth sum. So what he’s actually done here is to find the index of the term that is equal to 200,000, instead of the term that makes the total equal to 200,000. (Actually, he made a small mistake in his algebra; can you find it? We won’t mention it to him, because this is the wrong thing to be doing anyway.)
Correcting the equation
Doctor Rick replied, pointing out the main error and then starting the correct work:
OK, now I know that you are not familiar with the quadratic formula. You see how important it is for us to find out what a student knows, in order to provide the right kind of help. Perhaps you can tell me what kind of class you are in, and what you have learned so far in that class … assuming this is for a class.
There are other ways to solve a quadratic equation besides the quadratic formula, but we aren’t ready to think about that until we have written a quadratic equation. Let’s look at what you did so far:
an = a1 + (n – 1)d
Sn = a1 + (n – 1)d
200,000 = 3260 + (n – 1)10
Somehow you copied the same formula twice. The first formula tells us how to find the nth term of an arithmetic sequence, given the first term (a1) and the common difference (d). We can’t use the same formula to find Sn, the sum of the first n terms of the sequence. What you wrote earlier was correct:
Sn = (n/2)(a1 + an)
The trouble is that in order to find Sn using this formula, we need to know the first term a1 and the nth term an; and we don’t know an yet! However, we do have a formula for an. So … and this may be where I confused you … what we can do is to replace an, in the formula for Sn, with the formula for an. Here’s what I get when I do that:
Sn = (n/2)(a1 + (a1 + (n – 1)d))
This can be simplified to obtain a nicer formula for Sn in terms of n, a1, and d. (Some students may memorize that formula; I don’t — I reconstruct the formula from yours, when I need it, just as I am doing now.) Or you could plug in the numbers you know right now, and then simplify the result.
If you do that correctly, you will have a quadratic equation in n. This will be the time to talk about quadratic equations and how to solve them. So let’s see what equation you come up with, and I’d like you also to tell me what you know about quadratic equations.
Daniel never replied, so we don’t know whether this start was enough, or what other tools are in his toolbox. But we can continue from here.
Simplifying the equation
First, let’s simplify the formula: $$S_n= \frac{n}{2}(a_1+(a_1+(n-1)d))= \frac{n}{2}(2a_1+dn-d)= \frac{1}{2}(dn^2+(2a_1-d)n)$$
Now we need to use the numbers from the problem (which we could have used earlier, if not for the desire to see if this is a memorable formula): \(a_1=3260, d=10, S_n=200,000\). Our equation becomes $$\frac{1}{2}(10n^2+6510n)=200,000$$ We can distribute the fraction and get $$5n^2+3255n=200,000$$ Now we can subtract 200,000 from both sides, and divide by 5:$$n^2+651n-40,000=0$$
We could try to factor this, but (knowing about the discriminant) I know that will be a waste of time. As a result, I strongly suspect that Daniel was expected just to use trial and error.
Using the quadratic formula
But we can use the quadratic formula, which says that the solutions to \(ax^2 + bx + c=0\) are $$x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$$ Taking \(a=1, b=651, c=-40,000\), we get $$n=\frac{-651\pm\sqrt{651^2-4(-40,000)}}{2} = \frac{-651\pm\sqrt{583,801}}{2} = \frac{-651\pm 764.0687}{2} = 56.53$$ (taking only the positive solution).
Of course, n has to be an integer! What did the problem ask for? “How many months will it take to reach 200,000?” We now know that the first whole number of months after which we will exceed 200,000 units is 57; at 57 months, we will have exceeded 200,000 units. Or we could say that during the 57th month we will reach the goal.
Let’s check the answer. First, to check the solution to the equation, we can take \(n=56.53\) and see that we get the right sum: $$S_n= \frac{1}{2}(10n^2+6510n)= \frac{1}{2}(10(56.53)^2+6510(56.53)) = 199,983.3545$$ This is less than 200,000 due to rounding. Rounding up, we get $$S_n= \frac{1}{2}(10(56.54)^2+6510(56.54)) = 200,021.558$$ So we have the right solution.
But we still need to find the amount added in that 57th month: $$a_n = a_1+(n-1)d = 3260+(57-1)10 = 3820$$
And now that we have that, we can confirm the sum: $$S_n= \frac{n}{2}(a_1+a_n) = \frac{57}{2}(3260+3820) = 201,780$$ which will be the first time over 200,000.
A trial of trial and error
Let’s do one more thing: How much work would it take by trial and error, as we now think Daniel needs to do it?
Our last attempt looked like this: $$a_{40}=3260+10(40-1)=3650\\S_{40}=\frac{40}{2}(3260+3650)=138,200$$
Doing that repeatedly would take more work than necessary. Instead, we can use our combined formula, $$S_n= 5n^2+3255n$$ Using that formula, our last guess (40) would be $$S_{40}= 5(40)^2+3255(40) = 138,200$$ as before. That’s still too small; let’s double our guess again (I’m not looking at the answer we found as I do this!). Taking \(n=80\), we get $$S_{80}= 5(80)^2+3255(80) = 292,400$$ That’s too large; let’s back off halfway to 60: $$S_{60}= 5(60)^2+3255(60) = 213,300$$ Still a little high, but not much; let’s decrease it to 55: $$S_{55}= 5(55)^2+3255(55) = 194,150$$ We went too far; let’s split the difference and try 57: $$S_{57}= 5(57)^2+3255(57) = 201,780$$ The only remaining possibility is 56, so we check that: $$S_{56}= 5(56)^2+3255(56) = 197,960$$ So we’ve found our answer: 57 months.
For a student who hasn’t learned the quadratic formula, this is still doable, but I wouldn’t consider it appropriate.

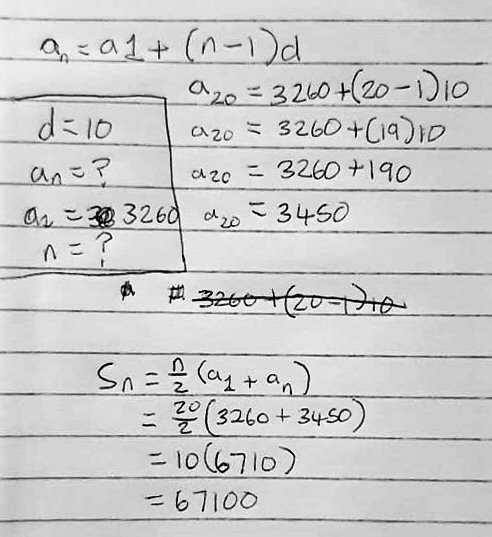
Re-reading this discussion I had with Daniel makes me wonder again how he could have been expected to solve this problem if he had never seen the quadratic formula. It seems unlikely that he would have seen, for instance, the method of completing the square without also seeing the quadratic formula. Perhaps he changed schools and was put into a class for which he hadn’t had all the prerequisites. Still, I got to thinking … Could we do better than basic guess-and-check in this situation?
Actually, first I was thinking about the question of whether the combined formula is in fact memorable. Doctor Peterson simplified it to
S[n] = (1/2)(dn^2+(2a[1] − d)n) [1]This can also be written as
S[n] = a[1]*n + dn(n - 1)/2 [2]which we can understand as follows: We start with a[1] in each of the n terms. We leave the first term alone, add d to the second term, add 2d to the third term, and so on. Thus we have n copies of a[1], for a total of a[1]*n, to which we add d(1 + 2 + 3 + … + (n-1)). In the parentheses we see the (n-1)th “triangular number”, whose formula is T[n] = n(n+1)/2, or T[n-1] = (n-1)n/2. The result is the formula [2] above.
Now, let’s make use of [2] to solve the problem by iteration. We have a[1] = 3260, d = 10, so
S[n] = 3260n + 5n(n - 1)and we want to solve the equation
3260n + 5n(n - 1) = 200,000I’ll factor out n on the left and divide both sides by 5 to start with:
n(652 + (n - 1)) = 40,000n(651 + n) = 40,000
What if we suppose that n is small compared to 651? Then we can approximate n by solving the equation
651n = 40,000The solution is n = 61.444. Now, use this value for n in that second factor:
n(651 + 61.444) = 712.444n = 40,000Solving this equation gives n = 56.1448. Once again using this value for n in the second factor, we get
707.1447n = 40,000n = 56.5656
It looks like we’ve got our solution to the nearest integer, in just three iterations! That’s not too bad …
But I really don’t think Daniel would have been expected to come up with this solution method.