(A new question of the week)
I like problems that can be solved in multiple ways, which can train us in seeing the world from different perspectives. Late in November we dealt with a pair of such questions involving angles in star-like figures.
A five-pointed star
Here is the first question, which was actually the second of two submitted at about the same time:
This one is hard question, no angles given.
We are supposed to find the sum of angles “A”, “B”, “C”, “D” and “E”.
Method 1: A bug’s eye view
Doctor Rick answered:
Hi, Daniel, thanks for writing to the Math Doctors.
Your problems are interesting. I can think of several ways you might approach each of them. I’d like to start with this one because I think it is a good introduction to one of the ideas I have in mind.
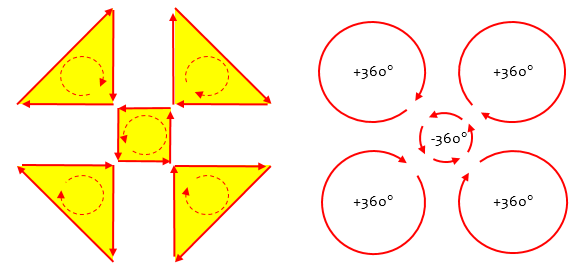
That idea is a little different from the usual way we think of geometry. Imagine that you are a bug crawling along the five-pointed star. Start on the horizontal line between A and B, just to make it more specific. You can crawl all the way around the paths (going straight through each intersection) and eventually end up back where you started. In doing so, you will have made five turns.
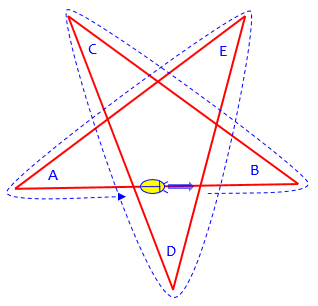
Now, I have two questions for you. First, by what angle do you turn at each corner (in terms of the angles A, B, C, D, and E)? Second, how many complete turns have you made by the time you get back to your starting point? (If you were crawling around a circle or a square or a pentagon, you would have made one full turn, or 360 degrees.)
If you can answer those questions correctly, then you can find A+B+C+D+E.
Here is one turn:
For comparison, here is what we would do with a pentagon:
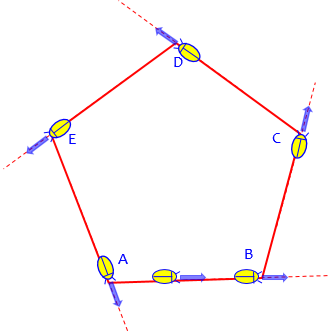
At each corner the bug turns, ultimately making exactly one complete turn in a circle. So the sum of all the turns is 360°. So what is the sum of the internal angles at those corners? It’s the sum of the supplements of five angles whose sum is 360°; so it’s \(5\cdot 180°-360°=540°\). More formally, we can write the equation $$(180-A)+(180-B)+(180-C)+(180-D)+(180-E)=360\\5(180)-(A+B+C+D+E)=360\\A+B+C+D+E=5(180)-360=540°$$
Method 2: Breaking it into triangles
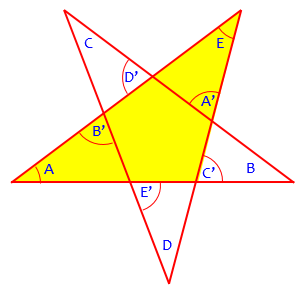
Here is a second, more traditional approach. Consider, for example, the triangle that has A and E as two of its angles. You can find the third angle in terms of A and E. Do the same with other triangles like this one, and use what you know about the interior angles of ordinary polygons (as opposed to star polygons like this).
Those are enough ideas to get you started, I think, since I presume you and your friend like challenges. You could apply similar ideas to your other problem.
First tries at both methods
Daniel tried both ways:
Ohhhh
Thank you very much Doctor Rick.
Just when I thought about the crawling rat thing I noticed I came back to the same point but in different direction.
Which means something like 180 degrees.
Also using the interior angles concept I could notice how a single triangle in the star could have the sum of two angles of another triangle which makes a + b + c + d + e.
In a single triangle! 🙂 and one triangle have sum of 180° so the star is likely to have total sum of 180° degrees in it.
I hope I didn’t get you wrong 🙂
The rat/bug approach is unclear here; Daniel has probably misunderstood something.
The triangle approach is not fully explained here, but upon reading carefully what he says and thinking about what he might be doing, I realize that he may have discovered a very nice way, and found the right answer. And in fact, looking ahead, we’ll find that he will explain it nicely later, so I’ll wait until then to make a picture of it. Can you see what he did?
Following the bug
Doctor Rick said,
If you would rather be a rat than a bug, that’s up to you. 🙂
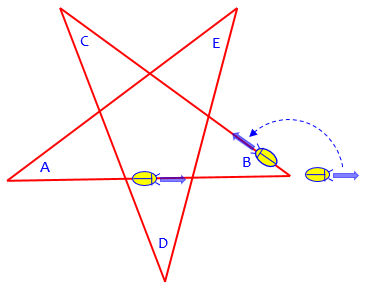
But I don’t understand what you mean by “I came back to the same point but in different direction.” Maybe you mean that you started at A and returned to A, but you weren’t yet facing right again, because you hadn’t yet made the fifth turn. I suggested starting in the middle of segment AB (taking these as names of vertices) so it would be clear that you had to complete all five turns.
It isn’t clear whether this is in fact what Daniel did; but let’s see what he would find if he did (sticking with the bug):
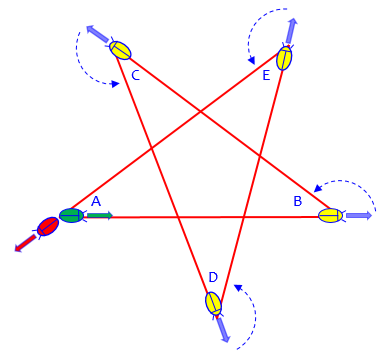
It started at A (green) and stopped when it got back to A, without making a final turn; since we don’t know the angles, we can’t know how far it turned.
Also, you didn’t really say how this led to an answer of 180°. I have to do some calculation before I’m done — notice that the turn at B, for example, is not by the angle measure B, but the supplement of that angle, as shown in the attached figure: the rat was facing right, and it turned through the angle I labeled β’ (beta prime) in order to crawl toward C. So, could you say more about how you got your answer by this approach?
Let’s finish this solution:
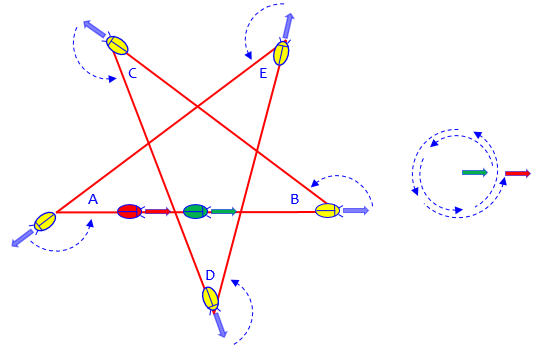
From the initial direction (green), the bug has rotated two full turns (720°) to the final position (red). Each turn is the supplement of the interior angle at that corner (e.g. \(180^\circ – B\)), so we can write an equation: $$(180^\circ – A)+(180^\circ – B)+(180^\circ – C)+(180^\circ – D)+(180^\circ – E)=720^\circ\\900-(A+B+C+D+E)=720\\A+B+C+D+E=180^\circ$$
So the sum of the five angles is indeed 180°.
Elegantly using the triangles
Again, I don’t follow your description of your thinking on the second method. How can you get a+b+c+d+e in a single triangle? You put a smiley there, and your words “likely to have” (and “something like” in the first approach) suggest that you know your thinking is too vague.
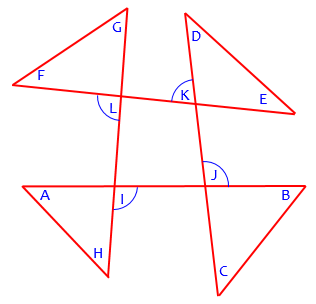
We’ll see what that meant soon. First, we need a better way to name the triangles:
In my figure, I named five points of intersection so that we can talk more precisely. For instance, what I was saying before was that α and ε (I used Greek letters for the angles) are two of the interior angles of triangle AGE, so that you can express the measure of angle AGE (which is the same as angle FGH in the pentagon) in terms of α and ε. You may be thinking of something different from what I did, which is fine, but you will have to express your thoughts more precisely in order to convince me that your method works. Would you like to try?
Daniel responded,
Hey there Dr. Rick
I am very-very sorry for my late reply.
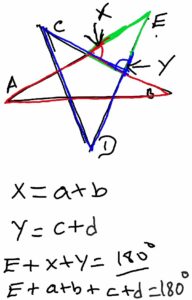
Anyhow, what I meant was if we look at the star as something formed from different triangles then use the exterior angles theorem (see the first image, here) we can notice how some exterior angles of some triangles exist in the closest triangle (see the second image, further down)
This Exterior Angle Theorem says that one exterior angle is equal to the sum of the other interior angles, and is very powerful.
For example:
The triangle that contains angle “A” and “B” (the one I colored red in my second image, here) have exterior angle in the triangle that contains angle “E” (the triangle I colored green). Also the triangle that contains angle “C” and “D” (colored blue) have an exterior angle in the triangle that contains “E”.
Now in exterior angles theorem *the exterior angle of a triangle is equal to the sum of the opposite interior angles* so in the triangle that contains “E” if we name the missing angles “X” and “Y” (see the second image in the attachment) so X would be equal to a+b and Y equal to c+d
So this way we got E + Y +X = 180° because the sum triangles interior angles is 180°
Y = C+D
X = A+B
Which means A+B +C+D+E = 180°
Because the sum of triangle interior degrees is doomed to be 180° 🙂
Sorry again for my late reply and sorry for the bad English.
Please let me know if there is something wrong with my way.
I really appreciate your will to help me!
This is excellent!
Doctor Rick answered:
Hi, Daniel. There is no need to apologize for delay in responding on a math problem. Your solution is very good — in fact, it is more elegant than either solution I had in mind. Did you come up with it on your own?
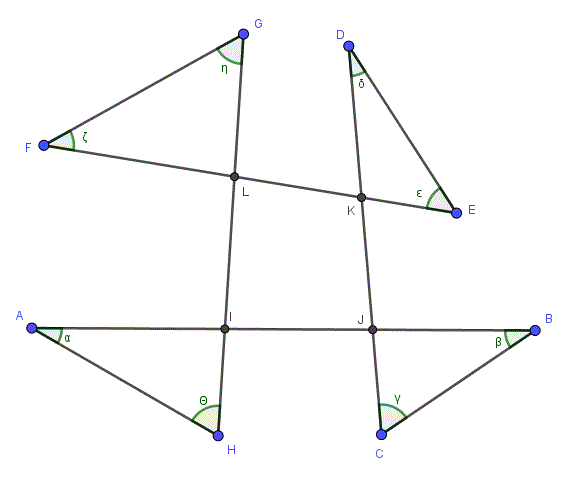
Using my figure (ignoring the extension of AB and angle β’), we can write a more formal proof of your result as follows:
By the Exterior Angle Theorem on triangle ABI,
m(∠HIE) = m(∠A) + m(∠B). . . . . . . . . [1]
By the Exterior Angle Theorem on triangle CDH,
m(∠EHI) = m(∠C) + m(∠D). . . . . . . . . [2]
By the Interior Angle Sum Theorem on triangle EHI,
m(∠HIE) + m(∠EHI) + m(∠E) = 180°. . [3]
Substituting from [1] and [2] into [3] gives
m(∠A) + m(∠B) + m(∠C) + m(∠D) + m(∠E) = 180°
You can’t get much simpler than this! — But to come up with a simple idea can take a good deal of thought. Good work!
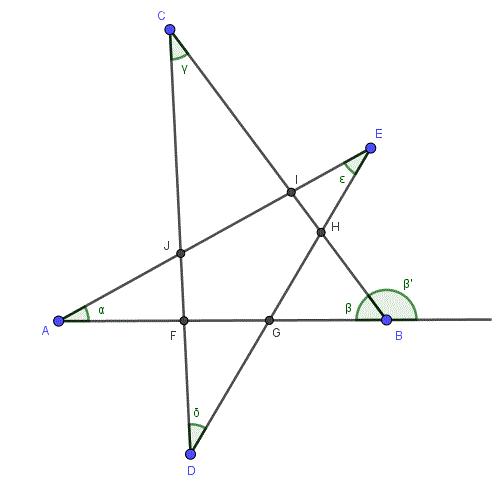
Here is a colored version of his picture to go with the proof:
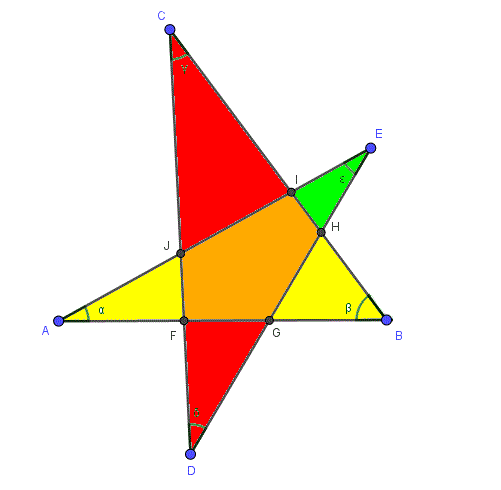
The angle in the green triangle at I is α + β; the angle at H is γ + δ; so the green triangle shows that α + β + γ + δ + ε = 180°.
Alternate triangle methods
I suspect the method Doctor Rick had in mind, using the sum of interior angles of polygons, looked like this:
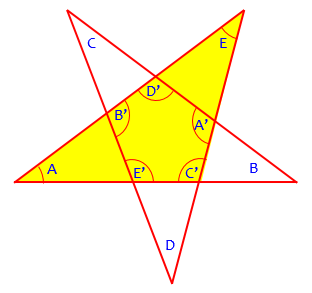
The Exterior Angle Theorem tells us that \(C’=180^\circ-A-E\), and similarly for the other interior angles of the pentagon. A theorem tells us that those angles add up to \((n-2)180^\circ\), so we can write the equation $$C’+A’+D’+B’+E’=\\(180-A-E)+(180-D-C)+(180-B-A)+(180-E-D)+(180-C-B)=3(180)\\900-2(A+B+C+D+E)=540\\A+B+C+D+E=180$$
Or, we could use the fact that the sum of the exterior angles of the pentagon is 360°:
This time, \(C’=A+E\) for the yellow triangle, and likewise for the others, so $$C’+A’+D’+B’+E’=(A+E)+(D+C)+(B+A)+(E+D)+(C+B)=360\\2(A+B+C+D+E)=360\\A+B+C+D+E=180$$
Now, if you were just asked for the sum of the angles in a multiple-choice context that implied the answer is independent of the specific angles, you might just adjust the figure so that it is inscribed in a circle, and assume (this can be rigorously justified, or you can just know this based on our other methods) that the sum of angles is unchanged. In that case, you can use the theorem about angles inscribed in a circle, that the inscribed angle is half the central angle of the subtending arc:
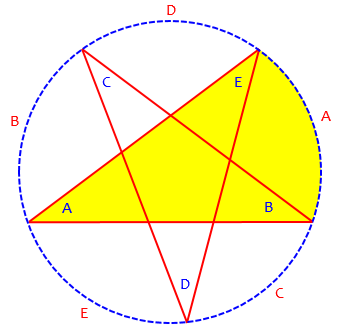
Here angle A is half of arc A, and so on; so the sum of the angles is half the sum of the arcs, which is 360°. And we’re done.
An 8-pointed … thingy
Two problems had been submitted at once. Here is the other, which Doctor Rick left unanswered to work on the easier one:
I got this question from a friend …
We are supposed to find the sum value of angle “a”, “b”, “c”, “d”, “e”, “f”, “g”, “h”
Please help us it is very urgent.
While Doctor Rick worked with the easier one, I wanted to suggest some ideas to supplement his:
Hi, Daniel.
I see that Doctor Rick is working with you on the pentagram question; I want to suggest some things to you that will apply ultimately to both problems. Here are pages I found at Ask Dr. Math that are relevant:
Measures of Interior and Exterior Angles of Polygons
The first suggests a variant on the “bug crawl” approach; the other two do essentially the same thing, in terms of the “winding number“, which is the number of times you wind around the center as you move around a figure. Any of these may give you additional perspectives on both problems.
For the problem in this question, you may be able to see exactly what the angles are (as drawn) just by thinking about the figure, and adding them up! Apart from that, you can break the figure up into four triangles and a square, label the unnamed angles in each, and write equations stating what the sum of angles in each triangle and the square are.
This last suggestion is similar to what I did above when I supposed that the sum would be the same as in the simpler case of an inscribed star (or even a regular pentagram). This yields lots of parallel lines, and you can see that the eight angles would all be 45°, making the sum 360°:
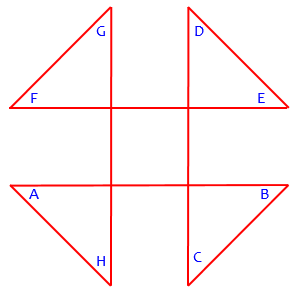
(This has been rotated and re-lettered so a bug would visit the vertices in order, as in the other problem.)
Doctor Rick added to this as well:
Hi, Daniel, Doctor Rick here. Let me point out a few things on this problem too.
First, as I understand it, you can’t assume anything about, for instance, whether lines are parallel, just because they look parallel. However, what Doctor Peterson said about just finding the angles and adding them up, assuming that the quadrilateral is a square (and maybe even that the triangles are isosceles), will give you the answer for that particular case — and the problem seems to imply, that the sum of the angles is independent of any details not given, like angles and lengths, so the particular answer is likely to be the general answer too.
That’s sort of cheating yourself, if you have a mathematical mind that really wants to know that the sum is invariant. But sometimes it’s helpful to find the answer first, and then try to prove it.
And that proof, as Doctor Peterson suggests, can be accomplished by either method I offered for the other problem. The work will be very similar to what I did there — which I haven’t exactly told you yet, I’ve just given hints. For this purpose I’ve attached a more general figure, marked up similarly to my figure for the other problem. I hope we can carry both problems through to your complete satisfaction!
The bug and its winding number
We didn’t hear back on this problem, because the other was where all the discussion happened. So let’s take a look at it.
First, here is the bug approach:
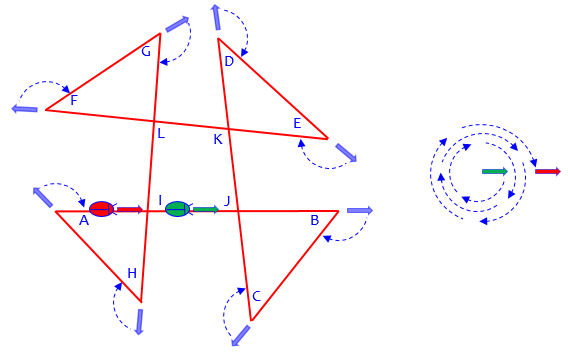
Following the turns, as I did on the right, we have three full turns (winding number 3), or \(3(360) = 1080^\circ\). This is the sum of 8 external angles; so the sum of the internal angles is $$8(180)-1080=1440-1080=360^\circ$$
An alternative way to count the turns is to observe that the four triangles are all circumnavigated clockwise, while the quadrilateral in the middle is covered counterclockwise, for a net motion of 3 clockwise:
Four triangles and a quad
If we break up into triangles and a quadrilateral, we find that the sum of angles A through H equals the sum of external angles I through L, whose sum is 360°:
That, I think, is about as elegant as we can get.

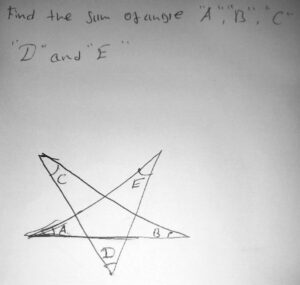
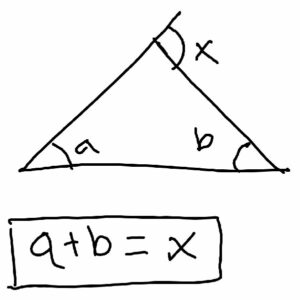
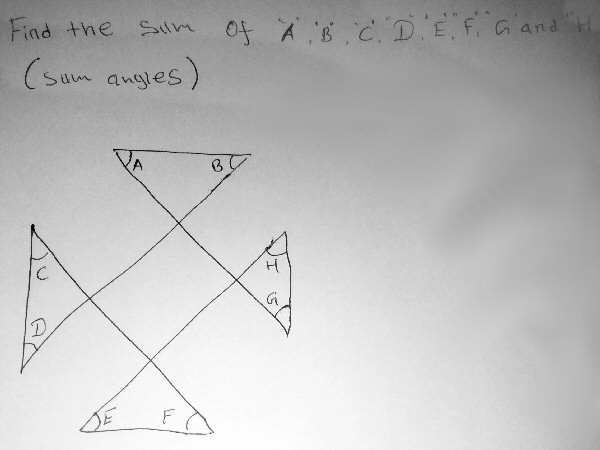
Hi.
Is the answer 54 degrees?
If the internal angles of a pentagon add up to 360 then divide that in 5 makes 72.
Making a large triangle with one of those angles and points A and E you can subtract 72 from 180, making 108, and divide that by 2 equals 54.
Ok so the interior angles of a pentagon add up to 540. So the answer is 36
Hi, Rich.
What question are you answering? Assuming you are referring to the pentagon problems, that question is about the sum of all five angles, not about any one angle; and it is nowhere assumed that the figure is regular, so there is no way to know what any particular angle is.
If you do assume a regular pentagonal star, then since the sum of the five angles is 180°, each of them is 180/5 = 36°. So your final answer is correct. As shown here, of course, there are many ways to determine that; your approach essentially uses the first figure under “Alternate triangle methods”, together with knowledge about the regular pentagon.
A mobius band is quite useful to explain pretty much everything in geometry
There might be ways to use it to explain things, but you’ll have to do the explaining! How do you see it as being relevant to these problems?
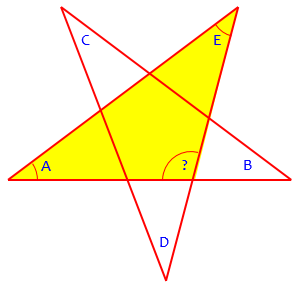
There is an even simpler solution, if you construct a line. However, it is not as generalizable.
Using the first diagram in Method 2, construct a line from the vertices of angles B and D. This now makes one large triangle that contains angles C, D, and B as well as two new angles next to D and B, call them d and b (In the large triangle C + D + B + d + b = 180°).
The opposite angle to angle “?” forms a triangle with angles d and b. Which means that A + E + ? = 180° and d + b + ? = 180°.
Therefore, C + D + B + A + E = 180°.
Hi, Bee.
Not bad. Here is an image to go with it:
In case a reader doesn’t see your final step, you are saying that A + E = d + b, because both are supplements of “?”, so we can replace d + b with A + E in C + D + B + d + b = 180°, resulting in C + D + B + A + E = 180°.