Because we have had a number of questions about vectors recently, I thought it might be time to look at various facets of that topic. Here, we will start with some ideas about what vectors, and their most basic operations, are. Next week, we’ll get into the far more interesting topic of multiplying vectors.
What is a vector?
We can start with this question from 2002:
What is a Vector? I am having trouble understanding exactly what a vector is and cannot seem to find a simple, straightforward explanation. Please help!
Patrick was only 10, so a fairly simple answer was appropriate. I answered:
Hi, Patrick. Vectors can be formally defined in several complicated ways, but I can give a basic introduction to the concept. Simply put, a vector is a directed quantity.
We’ll look at a more advanced view below. But here we need the basics.
One dimension: vectors on a line
We'll start with a one-dimensional vector. This is just the same as a number. Draw a number line, and draw an arrow starting at zero and ending at 5. This is the vector (5). Draw another arrow starting at the 5 and ending at the 8; this is the vector (3). It doesn't matter where a vector starts; all that matters is how long it is and how far it goes. So this second vector is 3 units long and points to the right, making it identical to a vector starting at 0 and going to 3. By putting two vectors end to end, as I did, I just added the vectors (5) and (3) to get the vector (8):
0 1 2 3 4 5 6 7 8 9
--+---+---+---+---+---+---+---+---+---+--
o------------------>o---------->
5 3
o------------------------------>
5+3=8
We can think of a vector in this sense as representing a motion. The vector (3) means “moving 3 units to the right”, regardless of where you start. And addition of vectors just means making one motion after another.
If you are familiar with negative numbers, you can see that a vector pointing to the left would correspond to a negative number. If we add the vectors (5) and (-5), we get the vector (0), a vector with no size at all. For any vector you draw, if you move it so that it starts at 0, it will point to its name. Since a one-dimensional vector is nothing but a (signed) number, it's nothing new. But this introduces the essential concept: only size and direction (left or right in this case) count, not position. Now we can look at two-dimensional vectors, in a plane, where things start to get interesting.
Two dimensions: vectors on a plane
Draw an arrow on a piece of paper, pointing in any direction, and you have a vector: a length with a direction. Draw another arrow starting at the tip of the first one, and you have added two vectors:
--+
/ |\
u+v / \v
/ \
/ \
o------------->o
u
If you draw vectors on a coordinate grid, you can give them names:
V(-2,3) ^ W(3,3)
+ | +
\ | / \
v\ | u+v / \v
\ | / \
\| / \
o------------->o------>
u U(5,0)
Here is that picture, slightly improved:
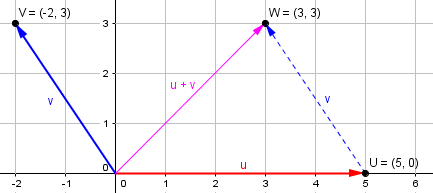
I’ve drawn the vectors u and v, both starting at the origin; then I’ve made a copy of v starting at the end of u in order to add them. This shows that \((5,0) + (-2,3) = (3,3)\):
Place each vector so that it starts at the origin (0,0), and name it for the point where it ends, just as we did on the number line. Our vectors are u = (5,0) and v = (-2,3), since they end at points U and V as shown. Their sum w = u+v is (3,3). Do you see how to add two vectors? You just add their x coordinates and their y coordinates; u goes 5 to the right and v goes 2 to the left, so w goes 5-2 = 3 to the right. (Actually, we use the word "coordinate" only for points; for vectors, we use the word "component.")
So for vectors with components \((a, b)\) and \((c, d)\), the sum would be \((a+c, b+d)\). In the example, walking 5 feet due east, then 2 west and 3 north, is equivalent to walking 3 feet east and 3 feet north. Addition produces the net result of two or more motions.
Three dimensions: vectors in space
You can do the same for vectors in three-dimensional space, but I won't bother drawing that. The important thing is that vectors give us a way to talk about anything that has both size and direction, but not position - things like velocities, wind speeds, forces, and so on. If I row my boat in the direction of vector u, but the water itself is moving along vector v, then I will actually be moving along vector u+v, so the sum of the two vector velocities tells me how fast, and in what direction, I am really going.
In three dimensions, we can still use components, like \((a, b, c)\), and we still add vectors by putting them end-to-end.
Magnitude and scalar multiplication
There are two specific ideas about vectors that are not explicitly mentioned there. One is that the magnitude (length) of a vector can be found by the “distance formula”. For a two-dimensional vector \(\mathbf{u} = (a,b)\), this is $$|\mathbf{u}| = |(a,b)| = \sqrt{a^2+b^2}$$
Second, in addition to being able to add vectors, we can multiply a vector by a number (called a scalar to distinguish it from vectors) in the obvious way: Doubling a vector would mean adding it to itself, doubling each component, and generally $$k\mathbf{u} = k(a,b) = (ka,kb)$$
At a (much) higher level, this basic picture of vectors expands into the more abstract concept of “vector spaces”, just as numbers expand from what you learn in kindergarten (1, 2, 3) into real numbers and beyond. Here is a question from a month after the last question, asking how this fits with the elementary definition:
Definition of a Vector
More on adding vectors
Now we need to examine further how vectors are combined. Here is a question from 2010:
Magnitudes of Vectors Don't Add Up I don't understand how adding vectors results in a triangle in which the third side is equivalent to the sum of the original two vectors. In particular, I don't understand how the sum of the two added vectors can have the same magnitude as the vector sum. A vector is defined as something with magnitude and direction, so vectors are equal if and only if they have the same magnitude and direction. The addition of vectors means combining two vectors, so the result of vector addition should give a vector with the same direction and magnitude as that of the combination of the added vectors, right? I can see how the sum of vectors A and B, if combined, would have the same direction as the third side of a triangle. What I don't understand here is how the magnitude of the third side can be equal to the magnitude of the other two sides. That would mean two sides of a triangle sum to the third side, wouldn't it?
The fact is, the magnitude of the sum can’t equal the sum of the magnitudes, so David has misunderstood something. Doctor Ian answered:
Hi David, Suppose you are standing on a giant grid. You are given two numbers (a,b). You move a units to the east, and b units to the north. Now you are given two more numbers (c,d). You move c units to the east, and d units to the north. What is the total distance you've moved to the east? It's a + c, right? And what is the total distance you've moved to the north? It's b + d, right? So you could have got to the same final point by being given the numbers (a + c, b + d) along with the same instructions. Does this make sense? Do you see how it illustrates the rule for vector addition?
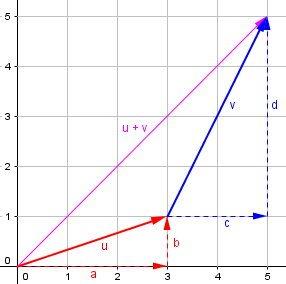
In this example, we are adding \((3,1)+(2,4) = (3+2,1+4) = (5,5)\).
Now Doctor Ian comments on two of David’s specific questions. First:
"A vector is defined as something with magnitude and direction, so vectors are equal if and only if they have the same magnitude and direction. The addition of vectors means combining two vectors, so the result of vector addition should give a vector with the same direction and magnitude as that of the combination of the added vectors, right?" Right. And they are combined by adding their components, as illustrated in the example above.
Don’t misread this: The direction and magnitude of the sum (resultant) is the direction and magnitude of the combination, not the sum of their magnitudes.
Next:
"I can see how the sum of vectors A and B, if combined, would have the same direction as the third side of a triangle. What I don't understand here is how the magnitude of the third side can be equal to the magnitude of the other two sides. That would mean two sides of a triangle sum to the third side, wouldn't it?" The magnitudes don't add directly. If you add two vectors, the magnitude of the resulting vector will be somewhere between zero and the sum of the individual magnitudes. The latter occurs when they have the same direction, e.g., (3,0) + (4,0) = (7,0) The vectors on the left have magnitudes of 3 and 4, and the sum has a magnitude of 7.

The former occurs when they have opposite directions, but the same magnitude, e.g., (3,0) + (-3,0) = (0,0) The vectors on the left have magnitude 3, but they cancel each other out, leaving a null vector, with no direction or magnitude.
![]()
His statement about the possible magnitudes of the sum can be strengthened to the “triangle inequality”, which we’ll see soon. We’ll see that the smallest possible magnitude of the sum is the difference of the individual magnitudes. It was zero in this case only because the two magnitudes were the same.
In between, we might have something like (3,0) + (0,4) = (3,4) Here, the vectors on the left have magnitudes 3 and 4, but the sum has a magnitude of 5. That would correspond to a situation like Two guys are pushing on a box. One pushes to the east with a force of 3 lbs, while the other pushes to the north with a force of 4 lbs. What is the resultant force on the box? We can add the vectors to get (3,4). The magnitude of that is sqrt(3^2 + 4^2) = sqrt(25) = 5 The direction of that is tan^-1(4/3) = about 53 degrees So we could replace the two guys with one guy, pushing with a force of 5 lbs, at an angle of 53 degrees from the x-axis, and the box would move in the same way as when the two guys push it. Now, why doesn't the combined force have a magnitude of 7 lbs? Well, think of it this way: the box is moving at an angle to the force being applied by the guy pushing to the east. So only SOME of his force is going to moving the box. And the same is true for the guy pushing to the east. So we should expect the resultant force to be less than either of the individual forces.
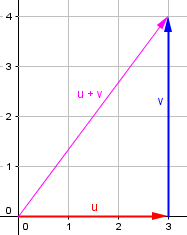
Now try thinking about those other kinds of cases. In one, the two guys are both pushing east, and their forces add up -- so the box moves to the east, under a force of 3 + 4 = 7 lbs. In the other, one guy is pushing east while the other pushes west, and since they apply the same magnitude of force, the box doesn't move at all. That is, it's like a force of 3 + -3 = 0 lbs is being applied to it.
So the magnitude of the resultant depends on how much the original vectors are “helping each other” or “fighting each other”.
In terms of triangles, you can think of it this way. The hands of a clock always form two sides of a triangle, right? And the third side of that is the line connecting the hands. Would you expect the length of that third side to always be the sum of the lengths of the individual hands? Or does the angle between them have something to do with it?
My guess is that David’s difficulty was largely in confusing “the magnitude of the combination” with “the sum of the magnitudes”.
Visualizing the sum: triangle inequality
Finally, here is a 1996 question about sums of vectors:
Sum of Two Vectors My daughter is having trouble learning about vectors. How do I explain the concept that the sum of two vectors a+b can be equal to or less than the sum of vector a + vector b ? To put it another way |a + b| <= |a| + |b|. I tried to explain it in terms of force being applied in the same direction, vs. in slightly different directions. However, no success yet. Is there an easier way to express or prove this relation to be true?
Note that what this (anonymous) parent says is missing a word: It is the magnitudes, not the vectors themselves, that are involved in the inequality. The symbolic form makes this clear.
Doctor Tom answered, changing the image from invisible forces to tangible motions:
I'd avoid a concept like "force," which may seem vague to her. Why not this: I start at home and walk 3 miles in a fixed direction. Then I walk 4 miles in a fixed direction, but not necessarily in the same direction as the first walk. How far from home am I? It's easy to draw pictures with vectors to see all the possibilities. If you happened to continue in exactly the same direction, you'd be 7 miles away, but it should be clear that every other path will wind up closer than 7 miles. In fact, if you happen to make a 180 degree turn, you'll only wind up a mile from home.
If we walk the 4 miles in the same direction we walked the first 3, the total distance is 7:
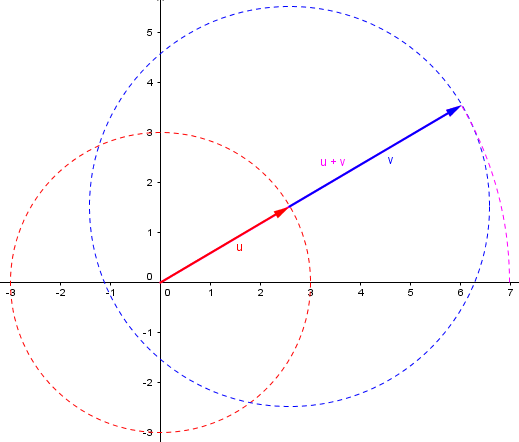
If we walk the 4 miles in the opposite direction, we end up 1 mile from the start:
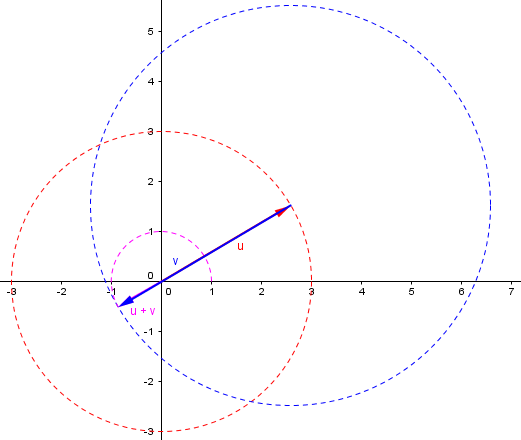
And we can end up any distance in between, such as 6 miles:
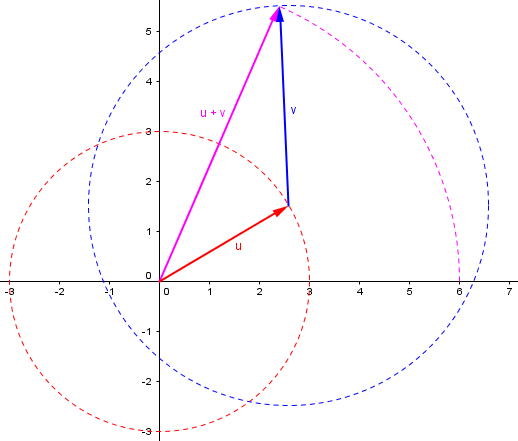
No point on the blue circle (possible end points) is farther than 7 miles from the start. And similarly, no point is closer than 1 mile from the start. This demonstrates the two sides of the Triangle Inequality: $$\left||\mathbf{a}|-|\mathbf{b}|\right|\le|\mathbf{a}+\mathbf{b}|\le|\mathbf{a}|+|\mathbf{b}|$$
This is called the triangle inequality because it is true of any triangle; each side is no longer than the sum of the lengths of the other two sides. Or, stated differently, a straight line is the shortest distance between two points.

Pingback: Vector Basics: Describing Directions – The Math Doctors
Pingback: Multiplying Vectors I: The Scalar Product – The Math Doctors