Unfamiliar Geometry Notation

(New Question of the Week)

One of the benefits of being a Math Doctor is interacting with the math of many cultures around the world, as we attract an international following. We have observed variations in terminology and notation from country to country, as well as variations in the content of math education (some better than what we know, some worse, some just different). It has become clear that the way we know math is not what everyone learns. Math may be universal, but the way it is expressed is not. (In what I write here, I will be reflecting my own perspective, having learned math in the U.S.; Math Doctors from Europe or other places may find what I call unfamiliar, totally normal!)

The notation

One thing that has particularly impressed me from some recent questions is the wonderful notation that is evidently used in Turkey (and presumably elsewhere) for lines in geometry, which I had never seen (or noticed, at least) until now, and like very much.  It is so clear and simple, and so consistent with other fields of math, that I can’t conceive of a better way. But I have not been able to find any information about it in order to be sure where it originated, how widespread it is, or why it is not better known in the English-speaking world.

[After writing this, I found a couple references indicating that it is used in Germany, and a similar notation is used in France. But why is it so hard to find any reference to it in English-language materials?]

We have received many questions from one Turkish student in particular recently. The problems themselves are often very interesting in themselves, but rather than focus on our discussion with him  about any one of these, I just want to look at a couple examples from a practice test he showed us.

Here are two problems, which I chose just because of the notation they demonstrate:

Problem 62:

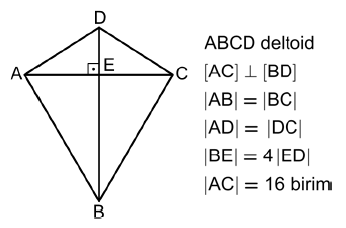
Şekilde ABCD deltoidinin alanı 160 birimkaredir.
Buna göre, ABCD deltoidinin çevresi kaç birimdir?

A) \(20 \sqrt{5}\)    B) \(24 \sqrt{5}\)    C) \(28 \sqrt{5}\)    D) \(30 \sqrt{5}\)    E) \(32 \sqrt{5}\)

Google translation:

ABCD deltoid
\([AC] \perp [BC]\)

\(|AB| = |BC|\)
\(|AD| = |DC|\)
\(|BE| = 4|ED|\)
\(|AC| = 16\) units

The area of the ABCD deltoid is 160 units.
How many units is the circumference of the ABCD deltoid?

A) \(20 \sqrt{5}\)    B) \(24 \sqrt{5}\)    C) \(28 \sqrt{5}\)    D) \(30 \sqrt{5}\)    E) \(32 \sqrt{5}\)

In other words, in kite ABCD, segment AC is perpendicular to segment BC; the lengths of AB and BC, and of AD and DC are equal; and the length of segment BE is 4 times the length of ED. The length of segment AC is 16 units. If the area of the kite is 160 square units, what is the perimeter of the kite?

We see here that \(\left[ XY \right] \), the notation we use in algebra for a closed interval, is used for a segment (where I am used to \(\overline{XY}\)). This is perfect: it means the set of all points between X and Y, including the endpoints. Similarly, \(\left| XY \right| \), the notation we use for the absolute value, or distance between points on a number line, is reused for the length of a segment (distance between points in space), where I am used to \(m\left(\overline{XY}\right)\), though many texts just use \(XY\).

Added 4/12/18: None of the examples I had readily available when I wrote this included all the notation I would have liked to mention. Two additional points are:

• The interior of a segment (that is, excluding the endpoints) is indicated by \(\left] XY \right[ \), which is the notation used in many countries for an open interval, ]A,B[, which we would write in America as (A,B).
• They indicate that a point is on a segment using set membership notation: \(M \in \left]XY\right[ \) means that point M lies on the segment XY, but not at an endpoint.

[We might quibble about the use of “units” rather than “square units” for the area, but perhaps “unit” here isn’t meant as a stand-in for a specific unit of length as in English math, but just refers to whatever unit (of length or area) is appropriate. Who am I to criticize someone else’s use of their own language? I have learned as a Math Doctor not to judge what may just be a difference of culture.]

Here is another:

Problem 64:

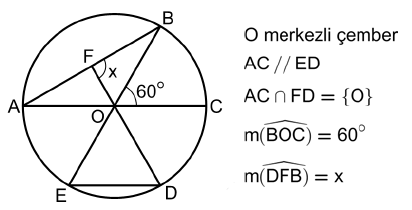
Yukarıdaki şekilde [AC] ve [BE], O merkezli çemberin çaplarıdır.
Buna göre, x kaç derecedir?

Google translation (probably could be improved):

O centered circle
\(AC // ED\)
\(AC ∩ FD = {O}\)
\(m(\widehat{BOC}) = 60°\)
\(m(\widehat{DFB}) = x\)

In the above [AC] and [BE], the center circle diameters.
According to this, how many are x?

A) 75   B)   80   C) 90    D) 105    E) 120

That is, we are given a circle with center at O, and know that line AC is parallel to line ED; line AC intersects FD at point O, and the measure of angle BOC is 60°; what is the measure of angle DFB?

Here, we see that \(XY\) without brackets represents a line (not restricted to points between X and Y), instead of requiring the difficult typography of \(\overleftrightarrow{XY}\); and the intersection of two lines is indicated by the usual symbol for the intersection of two sets. The notation for the measure of an angle is similar to that used elsewhere, and probably could be made more consistent.

[My searching suggests that in France, (XY) is used for a line, and XY for the length of a segment. This is a little less consistent, since as an interval, (a, b) does not continue past a and b; but it is nice in a way, as it suggests a lack of endpoints. I might perhaps suggest using <XY> for a line.]

The problems

We should take a moment to look at the problems themselves. No difficult geometry is required for these particular problems (some are much harder), but they are not routine, either. They require thinking in several steps, forcing you to find a path through the problem. Any questions? (If I get comments asking about them, we can discuss them!)

Okay, I’ll relent and show you one of the problems Sinan has asked us about, from a practice book for the test he showed us. Here is the question (which came with a sketch, but there is enough information here to make it yourself):

ABC is a triangle.
D is element of [AC]
|AB| = |AD|
|BD| = 24 units
|DC| = 7 units

What is the minimum value of perimeter of ABC as an integer?

My work:

ABC = 2a + 7 + |BC|
2a + 7 > 31
BC > 25

Perimeter of ABC > 56

But Book says 63.

He implicitly defined a = |AB|, and used the triangle inequality. Here is my answer:

When your answer is that the minimum is less than the claimed actual minimum, that tells you that you have not taken into account all conditions; adding another condition will tighten the “feasible interval”, making your assumed minimum unattainable.

What you have missed here is that 2a+7 does not have its minimum at the same time that BC has its minimum; one increases (toward infinity) while the other decreases (toward 25). So you can’t just combine the two inequalities.

I don’t have a formal solution, but just imagined that we adjust the length a = AB = AD while keeping BD fixed. When a is large, A is far from BD and DC approaches perpendicularity to BD, making BC smaller. When a is small, A is close to BD, and DC approaches collinearity with BD. Taking the latter to the extreme, A and C would lie on BD extended, making the perimeter equal 12 + 12 + 7 + 31 = 62. That is not a valid triangle, so the smallest integer value is 63.

This reasoning is not a proof; it is conceivable that as a increases, CD might decrease faster than 2a increases, so that there would be a smallest perimeter other than at the extreme. But a little more thinking convinces me that this would not happen; the rate of decrease of CD will be near zero at first.

One thing interesting here (and in several other problems Sinan sent us) is the restriction to integer values (asking either for the greatest or least, or the number of integer values possible). This makes it possible to have a multiple-choice problem that is hard to solve by working backward from the answers, since the integer answer may not in itself be significant. Also, at least the way I tend to solve them, it involves at least as much a feel for how geometry works, as it does formalism or proof.