Students sometimes wonder why the trigonometric functions (sine, cosine, tangent, secant, and so on) have the names they do, and how they relate to the corresponding terms in geometry. How are the tangent and secant functions related to tangent and secant lines in trigonometry? And what in the world is a sine? Here we’ll look at a few answers to those questions.
Where the words came from
We’ll start with this, from 1998:
Latin Origins of Trig Functions What are the origins of the words sine, cosine, tangent, etc.? Basically the six trigonometric functions: sin, cos, tan, csc, sec, cot.
Doctor Rick answered:
Hi, Kim. I've wanted to put together this information for some time. Thanks for getting me to do it! The following is based on etymological information from Webster's Third New International Dictionary.
I will refer to the following figure. O is the center of the circle shown passing through A and D.
* B
* D /|
*/ |
/ |* |
/ | * |
/ | * |
/ | *|
/ | *|
/ | *
/ | *
/_______________________|____*
O C A
We’ll be identifying each trig function applied to the angle \(\angle AOB\).
The word “sine” has the weirdest history:
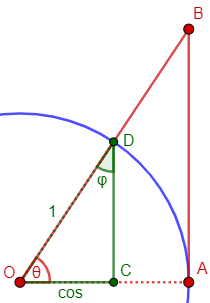
SINE comes from the Latin SINUS, meaning a bend or gulf, or the bosom of a garment. (We know the word from its anatomical meaning: the cavities or bays in the facial bones and from the names of some "bays" on the moon.) The term was used as a translation for the Arabic word "jayb," the word for a sine that also meant the bosom of a garment, and which in turn comes from the Sanskrit word "jiva" meaning a bowstring. The word was originally applied to the line segment CD in the figure: half the chord of twice the angle AOB. You can see how this could be called a "bowstring." The ratio of the sine CD to the radius of the circle, OA, is the SINE of angle AOB.
Here is the sine:
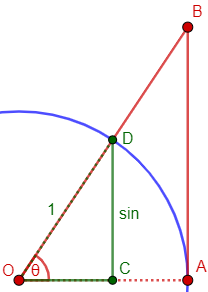
On a unit circle such as this, the sine of the angle is just the length CD; in general, it is the ratio of that side of the triangle (opposite the angle) to the hypotenuse, which is the radius of the circle.
Here we see the “bow” (arc) and the “bowstring“:
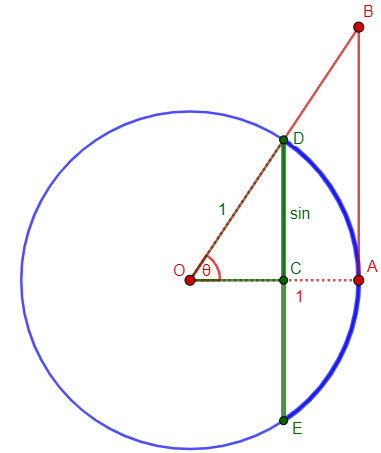
Incidentally, our word “archery” is related to “arc”, meaning “bow”; the entire bowstring is a “chord” (like the cord it is made of); and the segment CA is called the “sagitta”, or “arrow” (as in the constellation Sagittarius, the Archer). But we’ll see later how we got to a word for “bay” from a word for “bowstring”. It’s complicated! (And, no, it has nothing to do with the shore of a bay being shaped like an arc.)
TANGENT comes from the Latin TANGENS, the present participle of TANGERE, "to touch." In other words, it means "touching." It was originally applied to the line segment AB in the figure: the segment of the tangent to the circle at A that is cut off by the extension of OB. The ratio of the tangent AB to the radius of the circle, OA, is the TANGENT of angle AOB.
We’re familiar with the idea of a tangent line, touching the circle. Here it is:
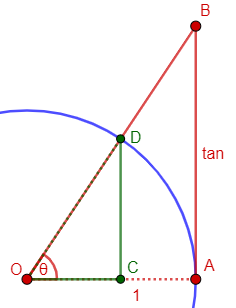
SECANT comes from the Latin SECANS, the present participle of SECARE, "to cut." In other words, it means "cutting." It was originally applied to the line segment OB in the figure - the line that cuts off the tangent. The ratio of the secant OB to the radius OA is the SECANT of angle AOB.
There are, of course, many lines that cut through a circle; this is a particular one, through the center. Here it is:
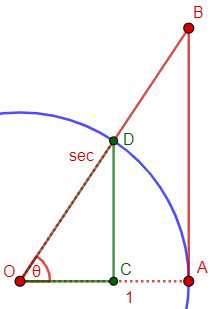
COSINE was originally written "co.sine," short for COMPLEMENTI SINUS: the sine of the complement. The COSINE of angle AOB is the sine of the complementary angle (ABO in the figure). Likewise COTANGENT and COSECANT are the tangent and secant respectively of the complementary angle.
Here is the cosine of θ, which is the sine of \(\angle OBA = \angle ODC = \phi\):
More details on the sine
This similar question from 1997 will fill in some gaps:
How the Trig Functions Got their Names I can guess why three of the trig functions are called cosine, cotangent, and cosecant. But why were the other three named the sine, the tangent, and the secant? Does the choice of the words tangent and secant have anything to do with the ordinary geometric meaning of these words?
Frank understands the “co-” part; Doctor Luis repeated what we’ve seen, then dug deeper:
Have you tried a dictionary? (you'd be surprised to know the number of things you can find out by using one). Webster's New Collegiate Dictionary suggests the following etymologies:
sine : Medieval Latin "sinus" from the Latin
word for "curve"
tangent: Latin "tangent-, tangens" from present
participle of "tangere" (to touch)
secant : New Latin "secant-, secans" from
present participle of "secare" (to cut)
Webster's II International has, for sine:
Latin sinus, a bend, gulf, bosom of a garment, used as translation of Arabic jayb, bosom of a garment, sine (in the latter sense from Sanskrit Jiva, bowstring, chord of an arc, sine).
He then quoted from Jeff Miller’s “Earliest Known Uses of Some of the Words of Mathematics: (S), showing the complicated route from Sanskrit to Arabic to Latin to English:
SINE. Aryabhata the Elder (476-550) used the [Sanskrit] word jya for sine in Aryabhatiya, which was finished in 499. According to some sources, sinus first appears in Latin in a translation of the Algebra of al-Khowarizmi by Gherard of Cremona (1114-1187). For example, Eves (page 177) writes: The origin of the word sine is curious. Aryabhata called in ardha-jya ("half-chord") and also jya-ardha ("chord-half"), and then abbreviated the term by simply using jya ("chord"). From jya the Arabs phonetically derived jiba, which, following Arabian practice of omitting vowels, was written as jb. Now jiba, aside from its technical significance, is a meaningless word in Arabic. Later writers, coming across jb as an abbreviation for the meaningless jiba, substituted jaib instead, which contains the same letters and is a good Arabic word meaning "cove" or "bay." Still later, Gherardo of Cremona (ca. 1150), when he made his translations from the Arabic, replaced the Arabian jaib by its Latin equivalent, sinus, whence came our present word sine. However, Boyer (page 278) places the first appearance of sinus in a translation of 1145. He writes: It was Robert of Chester's translation from the Arabic that resulted in our word "sine." The Hindus had given the name jiva to the half chord in trigonometry, and the Arabs had taken this over as jiba. In the Arabic language there is also a word jaib meaning "bay" or "inlet." When Robert of Chester came to translate the technical word jiba, he seems to have confused this with the word jaib (perhaps because vowels were omitted); hence he used the word sinus, the Latin word for "bay" or "inlet." Sometimes the more specific phrase sinus rectus, or "vertical sine," was used; hence the phrase sinus versus, or our "versed sine," was applied to the "sagitta," or the "sine turned on its side."
The two stories are basically the same. Similar mix-ups in translation happen all the time.
He went on to repeat essentially what we’ve seen about the tangent and secant:
The origins of the names tangent and secant are related to the circle. A line tangent to a circle is defined as a line that "touches" the circle at only one point. A secant line is a line that "cuts" the circle (it intersects the circle at two points). Now, the tangent and the secant trigonometric functions are related to the tangent and secant of a circle in the following way. Consider a UNIT circle centered at point O, and a point Q outside the unit circle. Construct a line tangent to the circle from point Q and call the intersection of the tangent line and the circle point P. Also construct a secant line that goes through the center O of the circle from point Q. The line segment OQ will intersect the circle at some point A. Next draw a line segment from the center O to point P. You should now have a right triangle OPQ.
Here is his picture, the same as before but labeled differently:
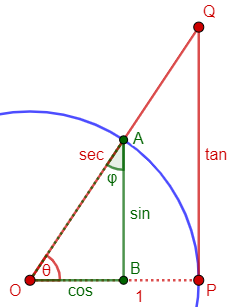
A little thought will reveal that the length of line segment QP on the tangent line is nothing more than the tangent (trig function) of angle POQ (or POA, same thing). Also, the length of the line segment QO on the secant line is, not surprisingly, the secant (trig function) of angle POA.
Now construct a line perpendicular to the line segment OP from point A. Call the intersection of these lines point B. You can readily see that
BA = sin POA
OB = cos POA
Can you find the other trigonometric functions?
He also tacked on more about the cofunctions:
As for the origin of the names for the co-functions, the reason comes from the following obvious fact:
If you have a trigonometric function trig(x), then the cofunction of trig(x) is
cotrig(angle) = trig(co-angle)
where co-angle is the "angle complementary" to angle. (Remember that two angles are complementary if their sum is 90 degrees)
So, the trig cofunction of an angle is the trig function of the complementary angle.
It is easy to see that in right triangles, the co-angle of an angle is the other angle (the third angle is already 90 degrees!). That's why cofunctions have the following properties, (try to prove all of them from a right triangle)
cos(x) = sin(90-x) (of course, x is in degrees)
sin(x) = cos(90-x)
cosec(x) = sec(90-x)
sec(x) = cosec(90-x)
cotan(x) = tan(90-x)
tan(x) = cotan(90-x)
Why isn’t the secant the reciprocal of the sine?
Approaching the question from a different direction, we have this from 2002:
Sine and Secant When someone applied the terms sine, cosine, tangent, secant, cosecant, and cotangent to the trigonometric functions, why didn't they make secant the reciprocal of sine and cosecant the reciprocal of cosine instead of the other way around, with cosecant being the reciprocal of sine and secant being the reciprocal of cosine? Why don't they just do it like they did with cotangent being the reciprocal of tangent? It would make it a lot easier to remember, don't you think?
This is a common thought of students: The secant is defined so that \(\sec(\theta)=\frac{1}{\cos(\theta)}\); why isn’t it instead \(\sec(\theta)=\frac{1}{\sin(\theta)}\)? Wouldn’t it be more consistent if the reciprocal of a non-cofunction was a non-cofunction? Not really.
I answered:
Hi, Vaughn. If you saw where the names come from, as in Origin of the Terms Sine, Cosine, Tangent, etc. http://mathforum.org/library/drmath/view/52578.html then you know why secant IS called secant. Since there is a reason to call it secant, there is no reason to call it the cosecant.
The link is to an answer by Doctor Rick very similar to our first one above.
You are supposing that trig functions ought to be named in such a way that "co's" are reciprocals of other "co's". But there's no such rule; the only general rule is that
co-f(x) = f(90-x)
(in degrees). That is, the "co-something" is the "something" of the complement. That's how tangent and cotangent are related, though they also happen to be reciprocals. There is no naming convention that indicates which functions are reciprocals. (But I'll suggest below that it really is more consistent than you realize.)
I have to admit that I once had the same sense of incoherence in the names.
The name "secant" refers to its representing the length of the secant line OB in Dr. Rick's picture. If we gave the name cosecant to that function, then the secant would not be the length of a secant line. In fact, there is no line you can draw on that picture, without a lot of contortions, that would represent the cosecant; so it is natural to give primary names to the functions that do have a simple meaning (sine, tangent, and secant), and to name the other three as co-functions of those.
It isn’t quite true that only the basic three have simple meanings. I’ve seen pictures that show all six basic functions as specific line segments, though they tend to be hard to follow. Here is a particularly nice version, from an MIT course:
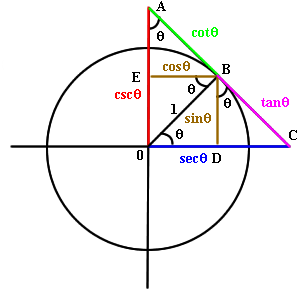
One nice feature of this arrangement is that the base functions are clustered near the x-axis, and the co-functions are clustered along the y-axis. Also, various identities can be seen by observing, say, the similarity of \(\triangle OBD\) and \(\triangle OCB\) to show that \(\sec(\theta)=\frac{1}{\cos(\theta)}\), or by applying the Pythagorean theorem to each of \(\triangle OBD\), \(\triangle OCB\), and \(\triangle OAB\) to prove the Pythagorean identities.
It suggests less familiar identities as well; for example, applying the Pythagorean theorem to \(\triangle BCD\) yields $$\sin^2(\theta)+(\sec(\theta)-\cos(\theta))^2=\tan^2(\theta).$$
This picture probably doesn’t represent the historical motivation for all the functions, and the tangent looks like only half a tangent line, but it’s nicely consistent.
For even more functions in one picture (many of them mostly forgotten in history), see here (Scientific American).
What's happening here is that, whereas trigonometry started in geometry, with each function having a clear relation to a circle, you now look at it just as arbitrary functions and expect the names to follow an abstract pattern that tells you what they mean from the name alone. If we were to start over and give names to the functions based only on their relation to the sine and cosine, we could certainly come up with a scheme that would meet your expectations; and it might be easier to work with, now that nobody thinks in terms of Latin names for parts of a diagram. But historically it makes perfect sense how the names are assigned, and it's not really hard to memorize their relationships. For one thing, it's convenient that the reciprocal of any "non-co" function is a "co" function. I find that actually easier to follow than if it were the other way. Here is a diagram that illustrates the relationships:
sin cos
\ /
tan ---+--- cot Opposites are reciprocals
/ \
sec csc
<------------->
complements
For instance, if I forget the reciprocal of the sine, I can just remember that it must be co-something, and it can’t be cosine; it can’t be cotangent, because that’s the reciprocal of the tangent, so it must be … cosecant.
Picturing the tangent: Quadrant I
Here is a basic question from 2001:
Why Sine, Cosine, and Tangent? Why is sine=opp/hyp, cos=adj/hyp, and tan=adj/opp? I know these things, I just want to know why!
Doctor Rob answered, largely repeating what we’ve seen. He first provided a link about sine, then made a picture for tangent:
Tangent is a lot easier to explain. Start with a unit circle with center O. Draw two radii OA and OB making angle x. Draw the tangent line to the circle at point A. Extend the radius OB in both directions until it meets that tangent line at point C.
|
o C
/|
/ |
/ |
/ |
sec(x)/ |
/ |
_,-----. o B |tan(x)
,-' / `-. |
,' / `. |
/ / \|
/ / x |
: O o-----------o A
\ / 1 |
\ / /|
`. / ,' |
`-_ / ,' |
/`-......-' |
/ |
This is much like what we saw above, the main difference is that he shows a secant line, not just a ray.
Then the distance AC along the tangent line will be tan(x). (It is the ratio of opposite over adjacent in the right triangle OCA.) It is the length on the tangent line cut out by the angle x, hence the "tangent of angle x." The word "tangent" for the line touching the circle at just one point is derived from the Latin verb "tangere," to touch, and means "touching." There is a similar explanation for using "secant" for the ratio hypotenuse/adjacent. In this case, the distance OC, measured along the extended radius OB, is sec(x). (It is the ratio of hypotenuse over adjacent in the right triangle OCA.) The extended radius is a secant line, that is, a line cutting the circle in two points. "Secant," too, is derived from a Latin verb, "secare," to cut, and means "cutting."
Finally, about the co-functions:
All the "co-" trigonometric functions are related to the complement of the angle. For any angle x, the complement is 90° - x. Thus the cosine of an angle is the sine of the complementary angle: cos(x) = sin(90°-x), cot(x) = tan(90°-x), csc(x) = sec(90°-x). Thus "cosine" is a contraction of "complementary sine," and likewise for cotangent and cosecant.
Picturing the tangent: Quadrant II
We’ll close with this, from 1999, which isn’t about the names, but asks for a picture:
Sine, Cosine, and Tangent on a Circle This should be easy for you, but I'm stuck. Do you have any visuals of where the sine, cosine, and tangent are on a unit circle?
Doctor Rob answered with a picture like the other, but using an angle in the second quadrant:
Q _..-----.._
.+' `-.
,' |\ `.
,' | \ `.
/ | \1 \
/ | \ \
. sin(x)| \ .
| | \ x 1 |
+-------+------+--------------+ P
| R cos(x) \O |
. \ .
\ \ /|
\ \ / |
`. \ ,' |
`. \ .' |
`-._ _.-' |
''-----'' \ |tan(x)
\ |
x = <POQ, sec(x)\ |
|sin(x)| = length(RQ), \ |
|cos(x)| = length(OR), \ |
|tan(x)| = length(PS), \ |
|sec(x)| = length(OS). \|
o
S
The signs of each are determined by which quadrant x falls in. If x is in the first quadrant, then all are positive. In this picture, x is in the second quadrant so the sine is positive and the rest negative.
We think of the segments as signed lengths, so that the cosine shown is a negative “length” because it goes “backward” (left). The same is true of the tangent, which goes down rather than up/ The secant is negative because it goes opposite to the terminal ray of the angle.
I don’t normally think of geometrical meanings for these functions outside of the first quadrant, which is why this seemed important enough to include.
