Significant Digits: Introduction

Our next series of posts will be about the concept of significant digits (also called significant figures), which are important in scientific or engineering calculations to keep track of the precision of numbers (although, as we’ll see, they are not what you would use when you need to be especially careful). We’ll start with the general concept and how to count “sigdigs”, and next time move into how they are used.

What are significant digits?

Let’s start with a very simple question from 1998:

Significant Digits

What are significant digits?

Doctor Mitteldorf answered in terms of the need for them, which is an important place to start:

Whenever you make a measurement, the measurement isn't precise.  Scientists like to compare their experiments with a theory, and the measurement never agrees completely with the theory. But if the difference between the measurement and the theory is small, maybe the theory can still be right, and the error in the measurement accounts for the mismatch. This is the reason scientists are always thinking about error estimates when they make a measurement.

So significant digits are one way to keep track of how much accuracy you can expect in a calculation based on measurements, so that you can tell if an observation differs significantly from the theory being tested.

Say you measure the length of your classroom with a meter stick. You line up the meter stick and do it by eye, and you get 10.31425 meters. That last 25 represents a quarter of a millimeter.

When you think about the size of the error you could have made, you have to admit that you could be as much as 5 millimeters off. After all, the line you measured on might not have been exactly straight; the room isn't completely square, you eyeballed the ruler when you placed it end to end...

So you could say your measurement is 10.31425 meters with an uncertainty of .005 meters. It could be as much as 10.319 or as little as 10.309. That means that the 10.31 are the 4 significant digits; the fifth digit, the 4, is only slightly significant (since it could be as much as a 9) and the remaining digits aren't significant at all, and should be dropped, by convention, when you report your result. The 2 and the 5 don't really have any experimental meaning; they are not significant digits. The 4 is optional in this case.

As a result of this, we only want to write that measurement as 10.31 or 10.314; anything more implies that we are more certain than we really are, leading to possible false conclusions. We only want to write the digits that are significant, in the sense that they should be taken seriously.

As a result, when scientists or engineers write numbers, they mean something more than they mean to pure mathematicians: not only a value, but a level of precision as well. Mathematically, we would say that 10.310 means the same thing as 10.31, but in the context of measurements, the former implies a more precise measurement.

How are significant digits counted?

Many questions we get involve how to decide which digits are called “significant”, particularly when some of them are zero. It can be surprisingly difficult to answer that question clearly without digging deeply into the reasons for the answer (as we will be doing in a later post). Here is a question from 1999:

Significant Digits and Zero

What is the best way to explain significant digits? When are zeros significant and when are they not significant? What is the meaning of significant in regard to this concept? Certainly the zeros in the number 5,000 are important, but apparently not significant. How about 508? How about 23.0? How about 0.05? How about 46.50?

As we’ll see, 5000 is a special case; the other zeros are more clear-cut. I answered, focusing on how to distinguish significant from non-significant:

A digit is significant if it contributes to the value of the number. Since zeroes on the left (if they are to the left of the decimal point) can be dropped without affecting the number, they are insignificant. Zeroes on the right (if they are to the right of the decimal point) are considered significant because they tell you that that digit is not some non-zero value, as do zeroes between digits. Zeroes between the decimal point and non-zero digits, however, are present only to keep the other digits in the right place, and are not significant - they're certainly important to the number, but are there only as a scaffolding, not as part of the building.

We’ll be looking later into just what we mean by “contributing to the value of the number”. At this point, I’m giving a very informal description.

How about that 5000, where there is no decimal point?

In the case of a number like 5000, the zeroes are really ambiguous, since they might be there for either reason; when we pay attention to significant digits, we usually write numbers in scientific notation so that we don't have to write any zeroes in that position, and can avoid the ambiguity. On the other hand, if you wrote 5000.0, we would assume all the digits were significant, since decimal places are included that aren't just required to show place value. If you write 5000., it is generally taken to mean that all the zeroes are significant.

So, I might have measured only to the nearest thousand, so that only the 5 is significant; or I might have measured to the nearest ten, so that the first two zeros are significant.  In the former case, in scientific notation (called “standard form” in some countries) I would write \(5\times 10^3\), and in the latter \(5.00\times 10^3\).

In your examples, the significant digits are

    5000      (1 - though the zeroes
    =          COULD be significant)

     508      (3 - everything between
     ===       first and last nonzero digits)

      23.0    (3 - zero could have been
      == =     omitted, must have a purpose)

       0.05   (1 - zero couldn't be dropped,
          =    has no significance)

In general, significant digits are:

    000xx0xx000       Between first and last
       =====          non-zero digits

    000xx0xx000.000   Between first non-zero
       ============   digit and last decimal

    000xx0x.x0xx000   Between first non-zero
       ==== =======   digit and last decimal

    000.000xx0xx000   Between first non-zero
           ========   digit and last decimal

Placeholders as scaffolding

The next question, from 2001, gave me a chance to elaborate on that “scaffolding” image:

Significant Digits in Measurement

I understand that there are rules to determine the significant digits in measurement; however, I do not comprehend the basic concept behind the use of significant digits. It seems to me that all digits are significant, especially zeros for place value. An example of my confusion would be: How can 3000 have only one significant digit (3)? or How can 0.0050 have only two significant digits (50)?

We need to think more about what “significant” means, especially for zeros. I replied:

The basic idea is that all digits that are not there ONLY for place value purposes are significant. 

Suppose I built a building that rose 10 stories high, but the first two stories were just columns holding the rest up above a highway. The first two "stories" would be important, certainly; but they wouldn't really count as part of the building, because they only hold it in place, without actually containing anything useful. The building has only eight "significant stories"! Zeros used only for place value at the right of a number are mere scaffolding holding it "above" the decimal point, and don't really contain any information.

I’ll have more to say about this below. But the main idea is that in my building, the highest floor is 7 stories above the lowest, and that would still be true if we removed the columns at the bottom to make an 8 story building.

It's a lot easier to talk about significant digits when you write numbers in scientific notation, which is designed to neatly separate significant digits from the size of the number, by ensuring that no extra zeros are required in order to write it. 

If we write 3000 as 3 * 10^3, we can see we have only one significant digit. If I write it instead as 3.000 * 10^3, it has four, because I am explicitly telling you all four digits. When I write it as 3000, you can't tell whether the 0's are there because I know they are correct, or just because I had to put them there to write the number (placeholders). You really can't say just from looking at the number what I meant.

Similarly, if we write 5.0 * 10^-3, we clearly have two significant digits. In this case, that is just as clear from 0.0050, because you know the zeros before the 5 are there only as placeholders. If those digits were non-zero, I would have had to write their correct values, whereas if the zeros in 3000 were really non-zero, I have the option of writing them or rounding them off.

Scientific notation eliminates the need to write any digits as mere placeholders, so all the digits you see are significant (unless you write unnecessary zeros on the left, which would be silly).

This is one reason that serious science is commonly done entirely using scientific notation.

Going beyond rules

Now let’s jump to a 2007 question that asks the $1,000,000 question: What’s really going on here? It’s a long question, so I’ll quote it piece by piece. First:

Explanation of Significant Figures

My Physical Sciences teacher introduced our Honors class to the concept of "Significant Figures".  At first it wasn't a problem.  She made us take notes and include the book-given definition.  But then we got a graded worksheet back, and almost everyone got a certain question on significant figures wrong.  So, for the past two days, there has been a heated debate going on over significant figures.

Ultimately, here's my question: How can 1,000,000 have only one significant figure, but 1,000,000. have 7?  I understand that it's the decimal point, but saying that 1,000,000 has only one significant figure is coming across to me the same as saying that 1 = 1,000,000 because none of the zeros are important or "significant".  Also, my teacher asked two other teachers for information, and one mentioned the Atlantic-Pacific rule which "works most of the time", and the other said it works "only some of the time". 

What's going on here? And what's up with the whole 1,000,000 thing? And how many significant figures does .0549 have, and how about 0.0549?

To me, saying that 1,000,000 has only 1 SF, but 1,000,000. has 7 SF seems to me to mean the same as 1 = 1,000,000; but this doesn't make sense to me.  Having $1,000,000 is a lot different than having one dollar.

I wasn’t familiar with the “Atlantic-Pacific Rule”; it turns out to be a common mnemonic (in America only!), exemplified by this page:

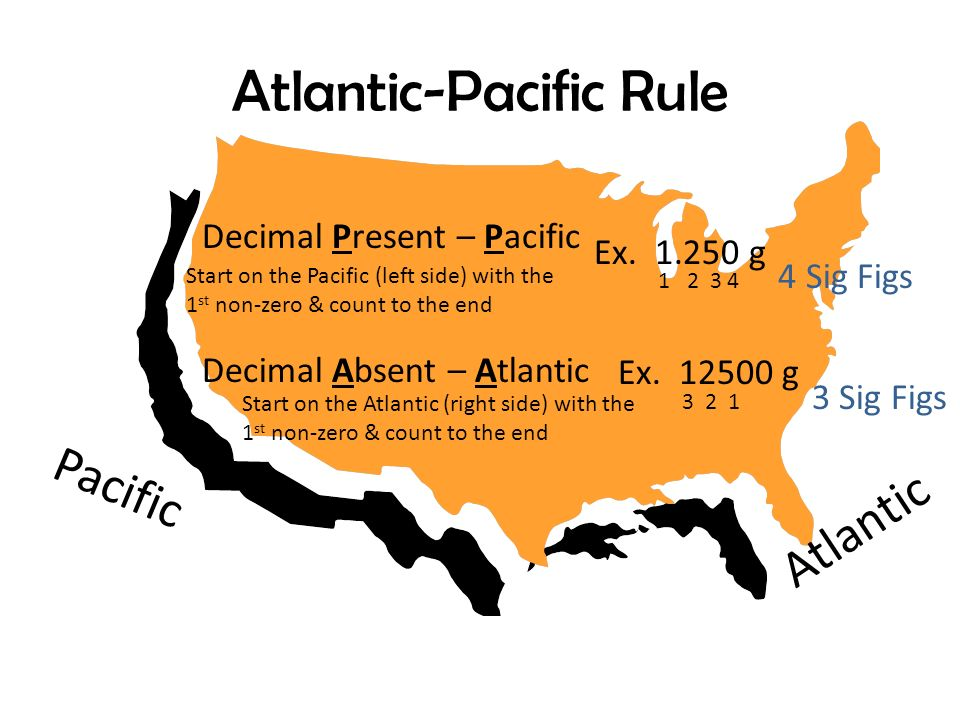
It agrees with the descriptions I’ve given; but like many mnemonics, it may distract students from thinking about the meaning of what they are doing, by focusing on the mechanics. And it entirely overlooks any ambiguity.

I started with the essential meaning of significant digits:

A significant digit is one that we can properly assume to have been actually measured.  We make such an assumption based on a set of conventions about how to write measurements: we only write digits that we have actually measured, unless the digits are zeros that we just have to write in order to write the number at all.  For example, if I use a ruler that shows millimeters (tenths of a centimeter), then if I wrote 12.34 cm I would be lying, because I can't really see whether that 4 (tenths of a millimeter) is correct.  If I wrote 12.30 cm, I would still be lying, because I would be claiming that I know that last digit is exactly zero, and I don't.  I have to write it as 12.3 cm.  All three of these digits are significant--they really represent digits I measured.  They are still significant if I write it as 0.123 m (just changing the units to meters), or as 0.000123 km (using kilometers this time).  Here, the zeros I added are there ONLY to make it mean millionths; they are placeholders.

So the concept is based on trusting that the writer would only write what is known. It is, of course, zeros that complicate this …

It isn't really quite true, as far as I am concerned, that 1,000,000 has one significant digit.  It MIGHT have only one, or it might have seven.  The problem is that you can't be sure; the rule of thumb that is being used doesn't allow you to indicate that a number like this has 2, or 3, or 6 significant digits.  Maybe I know that it's between 95,000 and 1,005,000, so that the first three digits are all correct, but the rules don't let me show that just from the way I write it.  I'd have to explicitly tell you, the value is 1,000,000 to three significant digits.

So someone who writes 1,000,000 has no way to indicate, within the numeral itself, how much of it to trust; so the convention is that we don’t trust the zeros. But someone could write 1,000,000 and tell us on the side that it is accurate to, say, the nearest ten-thousand (three significant digits), and that wouldn’t contradict the way it was written. This is what we mean by ambiguous. And this may be why some teachers said the rule doesn’t always “work”.

How to avoid the ambiguity? Use scientific notation:

Significant digits are really best used only with scientific notation, which avoids this problem.  We can write 1,000,000 with any number of significant digits:

  1: 1 * 10^6
  2: 1.0 * 10^6
  3: 1.00 * 10^6
  4: 1.000 * 10^6
  5: 1.0000 * 10^6
  6: 1.00000 * 10^6
  7: 1.000000 * 10^6

The trick is that we don't need any "placeholders" in this notation; every digit written is significant.

The ultimate point: relative precision

There was more to Forest’s question:

Is there a decent, constant rule about significant figures that I can remember?  And what makes "placeholders" unimportant, and what makes a number a "placeholder"?  0.0008 is a lot different than 0.08.  Again, how are these zeros unimportant???  I'm very confused on a lot of this, and right now I'm so confused that I can't even explain everything that I'm confused about!

I understand this:
 1) That 0.435 has only three significant figures.
 2) That 435 has three significant figures as well.
 3) That 4.035 has four significant figures because the zero has a 
digit of a value of one or higher on each side.

I'm not sure about the rest of the significant figures thing...If you have time, in your answer, would it be out of your way to touch on all "combinations" at least a little?  (By this I mean: 0.03 has ___ amount of SF because______, and 3.03 has... and 303 has... and try to get all of those?  Thanks!)

Good questions! I continued, talking about the real purpose of the convention:

The main idea of significant digits is as a rough representation of the RELATIVE precision of the number; that is, it is related to the percentage error that is possible.  For example, 0.08 indicates that the measurement might be anywhere between 0.075 and 0.085; a more sophisticated way to indicate this is to write it as 0.08 +- 0.005, meaning that there might be an error of 0.005 in either direction. This error is 0.005/0.08 = 0.0625 = 6.25% of the nominal value.  If you do the same thing with 0.0008, you get the same relative error; although the value itself is very different, the error is proportional to the value.  Both have one significant digit, which likewise indicates the relative error, NOT the actual size of the error.

This is the reason the zeros between the decimal point and the first non-zero digit are not significant: They don’t affect the relative error, because they change both the size of the number (each zero dividing it by 10) and the size of the possible error, in proportion.

We can also see this in terms of scientific notation. My example numbers are \(0.08 = 8\times 10^{-2}\) and \(0.0008 = 8\times 10^{-4}\), which both have one significant digit.

Rules and examples

He wanted rules, so I gave him rules (essentially the same as his Atlantic-Pacific rule, with the addition of ambiguity):

The significant digits of a number are all the digits starting at the leftmost non-zero digit, through the rightmost digit, if there is a decimal point.  If there is no decimal point, then you count only through the rightmost nonzero digit, because zeros beyond that MIGHT be there only to give other digits the correct place value.  (Zeros to the left of the first nonzero digit serve a similar purpose, but aren't counted anyway.)

Here are the cases I can think of:

Decimal point to the left of all nonzero digits: Count from the leftmost nonzero digit all the way to the end.

  .103   0.103  0.00103  0.0010300
   \_/     \_/      \_/      \___/
    3       3        3         5

Decimal point in the middle: Count from the leftmost nonzero digit all the way to the end.

  10.305  00103.0500
  \____/    \______/
    5          7

Decimal point on the right: Count from the leftmost nonzero digit all the way to the end.

  10305.  1030500.
  \___/   \_____/
    5        7

No decimal point: Count from the leftmost nonzero digit to the rightmost nonzero digit.

  10305  1030500 [here we don't know whether
  \___/  \___/..  the last 2 zeros are
    5      5?     measured or just placeholders]

Listing all the cases helped to reassure me that I wasn’t oversimplifying anything; in each case the rule agrees with the required meaning.

Forest replied,

Thank you so much for the help on Significant Figures!  I think I understand it now completely, and I liked the way you described everything...especially the examples.  Oh, and sorry for making you write all of those out...that probably took up a lot of your time.  But thanks again for the help!  The Dr. Math service is amazing and I always come out understanding whatever I had a problem with completely.  Great job!

It’s always encouraging when we can know we succeeded.

I’ll be looking deeper into the relative error interpretation in a later post, after we first look at how significant digits are used in calculations.