(A new question of the week)
Sometimes when we are learning a new subject, in this case calculus, a superficially simple question can be confusing. And that can be a good thing! Let’s look at a question about a derivative that, while not using very advanced concepts, gives a challenge to the learner that forces deeper thought about the concept, requiring distinctions that a routine question would not require the student to make.
The question came from Akhtar (father of a student), last August:
Dear Sir, Hi,
I have a question related to derivative (rate of change).
Suppose you are manager of a trucking firm and one of your drivers reports that, according to her calculations, her truck burns fuel at the rate of
G(x) = (1/200)(800/x + x),
G(x) = (1/200)((-800/x^2) + 1)
gallons per mile when traveling at x miles per hour on a smooth dry road.
- If the driver tells you that she wants to travel 20 miles per hour, what should you tell her?
- If the driver wants to go 40 miles per hour, what should you say?
I need guidance about the solution of this question.
In first part should we take x = 20 miles per hour in G'(x) to get G'(x) = -1/200 ?
Book answer is 1/200, go faster.
One thing is what does the minus sign tell us here.
Second part we get G'(40) = 1/400.
Book answer is G'(40) = 1/400, go slower.
Thanks in anticipation.
There are some points in the question to be clarified or corrected; and the problem itself, assuming it was reported fully, is a little unclear as to what kind of answer is expected. It was very helpful to be told what the book’s answers are, as that both helps us to understand the problem, and shows where Akhtar’s difficulty is. (Sometimes it turns out that a student’s only issue is that the book was wrong, and we don’t find out until the end of a confusing discussion!)
Doctor Rick answered, starting with a correction to the question:
Hi, Akhtar.
I was confused at first because you gave two different functions both called G(x). But when I started work on the problem, I realized that the second G(x) is actually G'(x), the derivative of the first G(x). I presume you accidentally omitted the prime.
So really, we are told that the fuel usage at x miles/hour is $$G(x) = \frac{1}{200}\left(\frac{800}{x} + x\right)\text{ gal/mi},$$ and the derivative of this is $$G'(x) = \frac{1}{200}\left(\frac{-800}{x^2} + 1\right).$$ This is the correct derivative, whether it was provided as part of the problem, or supplied by Akhtar as part of his work. (An interesting side question would be, what are the units of the derivative? It’s “gallons per mile, per mile per hour”, or \(\frac{\text{gal/mi}}{\text{mi/hr}}\) – a rate of a rate with respect to a rate, which will be part of the difficulty in this problem!)
We are not told the details of the student’s level of knowledge, but can make a guess:
It appears that this problem is presented in the lead-up to minimization/maximization problems, and maybe even before the student has become proficient at differentiation, since the problem gives the derivative. All that’s required of the student is to evaluate G'(x) for a particular value, and then to understand how the sign of G'(x) relates to the real world.
It isn’t quite clear what is actually being asked for, and what the first answer refers to; the “1/200” can’t be G(20), which is 0.3, so we have to interpret it as “G'(20) = 1/200”, which is not quite right. It’s -1/200, as Akhtar said. (Possibly, they really said that was the absolute value of the derivative.) The second answer gives us a clue about the goal: to decide whether it will be better to go faster or slower.
If the book’s answer to the first part said G'(20) = 1/200, that is incorrect; you got that part right. It’s the second task that is confusing you.
Notice what G(x) means: it is the rate of fuel consumption in gallons per mile at speed x miles/hour. What do you suppose the manager would like to achieve? I’d say he or she will want to save money by using less fuel on a given trip (of a fixed distance).
In light of this goal, can you see why in the first case you would tell the driver to go faster? If it still isn’t clear, tell me your reasoning and we can think further about it.
So we need to decide whether increasing or decreasing speed will reduce fuel usage.
Akhtar replied:
Thank you sir. If G(x) represents the rate of fuel consumption then what is G'(x)? Is it rate of change of fuel consumption? If so then G'(20) = -1/200 =-0.005 it is very low rate of change. So low consumption, then why we suggest to go faster.
In second part, G'(40) = 1/400 = 0.0025 so it is high as compare to first part so it is clear to go slower to save money by low consumption ….. but sir explain the first part.
Akhtar has evaluated the derivative and found that G'(20) = -0.005, while G'(40) = 0.0025. But he is interpreting these as if they were the rate of consumption, rather than the rate of change of the rate of consumption. This is not easy to interpret at first, particularly since the word “rate” is being used not as a rate with respect to time (as in miles per hour, as we are used to) but with respect to speed. It probably also doesn’t help that x here represents not position but speed! There are many things here that are unfamiliar, and require us to slow down and reevaluate what things mean.
Doctor Rick replied:
Yes, G'(x) represents the rate of change of fuel consumption (with respect to speed). If the rate of change were constant, G'(x) = -0.005 would mean that for every increase of 1 mile/hour in the truck’s speed, the rate of fuel consumption would decrease by 0.005 gallon/mile.
So G’ tells us not how much fuel we are using, but how much (and in what direction) that amount will change if we change our speed. Negative means the consumption will decrease (get better) if we increase our speed.
Likewise in the second part, for every increase of 1 mile/hour in speed, the rate of fuel consumption would increase by 0.0025 gallon/mile. That’s a smaller rate of change than in the first part (in terms of distance from zero, that is, the absolute value of G'(x)). So if the decision were to be made on the basis of how much the fuel consumption changes, there would be even less reason to change the speed in the second part than in the first.
Akhtar’s focus on the size (absolute value) of G’ is misplaced:
But the important part is the direction of the change, that is, the sign of the derivative. In the first part, going faster causes the rate of fuel consumption to decrease, which is what the manager wants. In the second part, going faster causes fuel consumption to increase; going slower causes fuel consumption to decrease. So in the second part the manager says to slow down.
This is where the answers come from. The best speed is greater than 20 mph, and less than 40 mph.
That’s sufficient to answer the question, but let’s consider your thought that G'(x) = -1/200 is “a very low rate of change.” We may not have a good feeling for the size of a rate of change of fuel consumption — that isn’t something we talk about often. To help us think about it, I’ve graphed G(x):
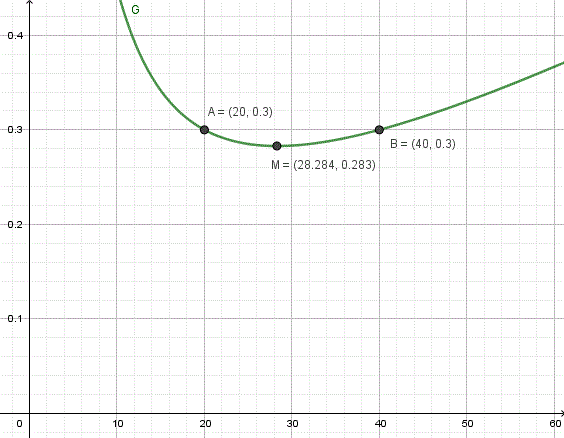
At x = 20 miles/hour (and also at x = 40 miles/hour), the fuel consumption rate is 0.3 gallons/mile. We could also say that the “mileage” of the truck at these speeds is 1/0.3 = 10/3 = 3.33 miles per gallon; that is, the truck will only go 3.33 miles on each gallon of fuel. (The mileage is a more familiar number to me, in the USA, and this is a very low number compared to that for automobiles, where we’d like to go 30 miles or more on a gallon of gasoline. I can believe, however, that 3.33 miles per gallon is reasonable for a large truck.)
So at both 20 mph and 40 mph, the fuel consumption itself is the same, and that is a relatively high number. (At 30 miles per gallon, the consumption would be 1/30 = 0.0333 gallons per mile, much less than in our story.)
Now compare with the minimum rate of fuel consumption, which I have found and labeled to be about 0.283 gallons/mile at a speed of about 28.284 miles/hour. By increasing the speed by 8.284 miles/hour, we have reduced the fuel consumption rate by 0.3 – 0.283 = 0.017 gallons per mile. If the truck goes 100 miles, we save 1.7 gallons of fuel. On that 100-mile journey, we use 28.3 gallons rather than 30 gallons, a saving of 5.7%, which the manager probably doesn’t consider to be negligible.
A small change in the fuel consumption can be very significant.
The way to find the minimum, you may see from the graph, is to find when G'(x) = 0:
$$\frac{1}{200}\left(\frac{-800}{x^2} + 1\right) = 0$$
$$\frac{-800}{x^2} + 1 = 0$$
$$x^2 = 800$$
$$x = \sqrt{800} = 28.284$$
The student at this point hasn’t gotten to the point of finding that minimum, and therefore being able to tell how much faster or slower to go, only the direction in which to change the speed to reduce fuel consumption. Yes, increasing speed by just 1 mile/hour won’t do much, but the saving adds up. I hope this helps.
So what have we learned?
When a problem is confusing, we need to decide what part to focus on, in this case the sign. We have to think carefully about what it means, and apply that to the goal. And that careful thought will hopefully lead to better understanding in the future.
