(A new question of the week)
We have had a lot of interesting questions recently. This one involved inverse trigonometric equations that led to cubic and quartic equations. We’ll observe here one of the benefits of embedding the original discussion in a blog format where I can add information that will help you, the reader, follow what we are saying, as we frequently answer at the level of the asker, not of bystanders! There’s a lot to fill in between the lines.
First problem, leading to a cubic equation
Here is the initial question (from the end of June):
Dear Dr. Math,
I’m a student currently doing my A levels. While finding solutions for the inverse trig function equation in attachment 1, I came to the step involving a 4-term equation of degree 3.
Though I’m familiar with quadratic and 3-term equations of degree 3, I don’t know how to solve this. I calculated the answer for both the trig equation and the other one in my calculator and got x = 0.5. But I don’t know how to get there. Could you please explain me how to solve the polynomial equation or if there’s a better way to solve the trig equation at the first place, I would be happy to know. It would be great if you could give some help.
Sithum
How did he get that cubic?
Before answering, I had to check that cubic, with no clue how Sithum got it. Fortunately, he appeared to have done just what I would do. I could leave that for you to do, too, but let’s go through it. The first step in many problems involving inverse trig functions is to turn them inside-out by a substitution. Let’s let \(\tan^{-1}x = \alpha\), so that \(\tan(\alpha) = x\), and \(\tan^{-1}\frac{2x}{7} = \beta\), so that \(\tan(\beta) = \frac{2x}{7}\). Then the equation becomes $$2\alpha – \beta = \frac{\pi}{4}$$ We also know that \(\alpha\) and \(\beta\) are in the range of the inverse tangent function.
Now we can take the tangent of both sides of this equation, and then apply the angle-sum and double-angle formulas to the LHS:
$$\tan\left(2\alpha – \beta\right) = 1$$
$$\frac{\tan(2\alpha) – \tan(\beta)}{1+\tan(2\alpha)\tan(\beta)}=1$$
$$\tan(2\alpha) – \tan(\beta)=1+\tan(2\alpha)\tan(\beta)$$
$$\frac{2\tan(\alpha)}{1-\tan^2(\alpha)} – \tan(\beta)=1+\frac{2\tan(\alpha)}{1-\tan^2(\alpha)}\tan(\beta)$$
$$2\tan(\alpha) – \tan(\beta)(1-\tan^2(\alpha))=1-\tan^2(\alpha)+2\tan(\alpha)\tan(\beta)$$
$$2\tan(\alpha) – \tan(\beta)+\tan^2(\alpha)\tan(\beta)=1-\tan^2(\alpha)+2\tan(\alpha)\tan(\beta)$$
Now we replace each tangent with its known value:
$$2x – \frac{2x}{7}+x^2\frac{2x}{7}=1-x^2+2x\frac{2x}{7}$$
$$14x – 2x+2x^3=7-7x^2+4x^2$$
$$2x^3+3x^2+12x-7=0$$
There’s the cubic equation.
How can we solve that cubic?
Now we have to solve it. I answered:
Hi, Sithum.
Good work so far; I got the same cubic equation, so I presume your method was similar to mine! I can’t see a better way.
As for solving the cubic, there are complicated methods (most of which I have rarely, if ever, actually used!), such as discussed here:
You have evidently learned the easier parts of that approach.
But in general, I would always either use technology (and then check whether the answer is exact), or start with the rational root theorem. The latter tells us to check just a few possible roots (by synthetic division), one of which is 1/2, and works. That’s what I did just now, and found that the other roots are non-real. So that’s my recommendation. It doesn’t by any means always work; but when a problem is assigned, in such a way that you have reason to believe the answer will be “nice”, then you can expect it to work.
The link is to our FAQ, which starts with a way to eliminate the \(y^2\) term, making a “3-term equations of degree 3” such as Sithum said he has learned how to solve. (The steps from there are even more complicated, but can be expressed as a formula.) We’ll be mostly talking about the method I suggested in my last paragraph, which is to first find a solution (either from a graph, or by guess-and-check, or by checking only a few possibilities provided by the Rational Root Theorem. If you are not familiar with it, you can read about it here:
Rational Root Theorem Rational Root Theorem Proof of the Rational Root Theorem
Sithum, successful using my method, replied, asking for help with the FAQ method:
Dear Dr. Peterson,
Thank you very much for the quick reply. The rational root theorem was really a lifesaver and I used it successfully on a few problems afterwards. I tried the link you gave me above but I got confused in assigning p for x.
“The next thing we do is to get rid of the x2 term by replacing x with (y – e/3)”
I can’t figure out how the e went missing afterwards.
To that, I answered,
As for the substitution in the FAQ, I found this answer I wrote that may be helpful:
You may be able to find some helpful examples by searching (at the bottom of that page) for the phrase “cubic equation” or the like. I don’t have time at the moment to search further.
Second problem, leading to a quartic equation
But Sithum also had a new problem that introduced a further challenge:
Also I got stuck in the last problem (attachment) of the exercise because it didn’t have rational coefficients, and when I rationalized the first and last coefficients by dividing by sqrt3 the rational root theorem didn’t work. It would sound weird but we are supposed to solve such problems using only a logarithmic table for ease of calculation. So please excuse me if I’m troubling you over a task I could easily put in to my calculator.
I just gave a quick answer to get more information while I had other things to do:
I’ll have to take some time to work on this problem. It may help if you show your work as far as you got, so (like last time) I can check my work against yours. I’ll want at least to see the cubic you got.
Getting to the quartic equation
Then Sithum replied with work:
Dear Dr. Peterson,
Thank you very much for helping me out. My work is in the attachment below.
Substitution to obtain integer coefficients
This looks very much like my work for the first problem. While I was busy, Doctor Rick joined in:
Hi, Sithum. If I may add a comment, your work looks good to me. Your polynomial equation is
√3 x4 + 4x3 – 6√3 x2 – 4x + √3 = 0
I observe that √3 occurs only in the coefficients of odd powers of x, and if it weren’t for those, we’d have all integer coefficients. This prompts the thought of making a substitution for x. Can you see what I am thinking?
I made much the same observation when I got back, before seeing Doctor Rick’s comment. Since any multiple of \(\sqrt{3}\) has the radical in all its odd powers but not its even powers, we can let \(x = \sqrt{3}u\). The equation then becomes $$\sqrt{3}(\sqrt{3}u)^4 + 4(\sqrt{3}u)^3 – 6\sqrt{3}(\sqrt{3}u)^2 – 4(\sqrt{3}u) + \sqrt{3} = 0$$
$$9\sqrt{3}u^4 + 12\sqrt{3}u^3 – 18\sqrt{3}u^2 – 4\sqrt{3}u + \sqrt{3} = 0$$
Dividing by \(\sqrt{3}\), we get the equation
$$9u^4 + 12u^3 – 18u^2 – 4u + 1 = 0$$
to which we can apply the rational root theorem.
A surprising shortcut
Before going into that, I first added a different perspective:
Hi again.
When I finally sat down to work on this problem, I observed something that you missed. You drew a triangle to find that tan(β) = (2x)/(x^2 – 1). Does that look familiar? I had, out of habit, drawn such a triangle for each angle, and the result was hard to miss in that form.
Using that fact led me to solutions for α and β. This led to a merely quadratic equation in x. Checking the two solutions showed that one was extraneous.
You can see this triangle in the upper right of Sithum’s work. What I had done, habitually, was to draw one of these triangles for each of the two angles:
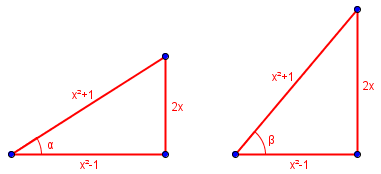
That is, if \(\cos(\alpha) = \frac{x^2-1}{x^2+1}\), and \(\tan(\beta) = \frac{2x}{x^2-1}\), then the two triangles are, in fact, the same triangle (even though I intentionally drew them differently to remind myself that they are two different angles)! The triangle Sithum drew actually applies to both angles, so (since they have to be in the same quadrant) \(\alpha=\beta\).
And since \(\alpha+\beta = \frac{2\pi}{3}\), we can conclude that \(\alpha=\beta = \frac{\pi}{3}\). Therefore, $$\frac{x^2-1}{x^2+1} = \cos\left(\frac{\pi}{3}\right) = \frac{1}{2}$$. This can be easily solved to yield \(x^2 = 3\), and \(x = \pm\sqrt{3}\).
Checking these two solutions in the quartic equation first, we get
$$\sqrt{3}(\sqrt{3})^4 + 4(\sqrt{3})^3 – 6\sqrt{3}(\sqrt{3})^2 – 4(\sqrt{3}) + \sqrt{3} = 9\sqrt{3} + 12\sqrt{3} – 18\sqrt{3} – 4\sqrt{3} + \sqrt{3} = 0$$
$$\sqrt{3}(-\sqrt{3})^4 + 4(-\sqrt{3})^3 – 6\sqrt{3}(-\sqrt{3})^2 – 4(-\sqrt{3}) + \sqrt{3} = 9\sqrt{3} + 12\sqrt{3} + 18\sqrt{3} + 4\sqrt{3} + \sqrt{3} = 44\sqrt{3}$$
so only the positive root is valid. (We could have determined this from quadrant considerations.)
How about the original equation?
$$\cos^{-1}\left(\frac{(\sqrt{3})^2-1}{(\sqrt{3})^2+1}\right)+\tan^{-1}\left(\frac{2(\sqrt{3})}{(\sqrt{3})^2-1}\right)= \cos^{-1}\left(\frac{1}{2}\right)+\tan^{-1}\left(\sqrt{3}\right) = \frac{\pi}{3} + \frac{\pi}{3} =\frac{2\pi}{3}$$
Solving the quartic
It works. And this should be the solution we get the long way. I continued, returning to Sithum’s work:
Then I checked my solution in your quartic equation, and found that it worked. So your equation seems to be correct, but yields even more extraneous solutions, at least in part due to the ranges of the inverse functions.
After that, I looked at how to solve your quartic, and made the same observation Doctor Rick did. Making the appropriate substitution, I got an equation with two rational roots, and two irrational roots. The four resulting solutions for x agree with the graph of your LHS, but, again, only one yielded a valid solution. (There’s a little more I want to think about, to make sure I didn’t miss anything.)
We are both intentionally not showing you the details, so you can have the pleasure of discovering them for yourself. It’s a very interesting problem!
Recall that our quartic equation after substitution was $$9u^4 + 12u^3 – 18u^2 – 4u + 1 = 0$$ The possible rational roots are \(\pm1, \pm\frac{1}{3}, \pm\frac{1}{9}\) Checking them by synthetic division, we quickly find that \(u=1\) and \(u=-\frac{1}{3}\) work. The quadratic quotient reduces to \(3u^2+6u-1=0\), whose two solutions, \(-1\pm\frac{2\sqrt{3}}{3}\), are real but irrational. Reversing the substitution, we find \(x=\sqrt{3},-\frac{\sqrt{3}}{3},2-\sqrt{3},-2-\sqrt{3}\). Checking these, we find that only the first (the one we found before) works.
Sithum closed the discussion:
Dear Dr. Rick and Dr. Peterson,
Thank you very much for putting so much effort to help me with the quartic. I’ll work out the problem and send my answers soon. Thank you again for all the help.
Yours
Sithum.
What lessons did we learn here?
Sithum already knew good techniques for solving inverse trigonometric equations, but perhaps you’ve learned something about that. Sithum also knew some things (seldom taught, in my experience) about solving cubics, but benefited from having the rational root theorem pointed out, and probably also from the substitution that made that applicable.
Yet it is quite possible that the lesson for which the problem was designed is mine about observing how very special it is. Sometimes we have to keep our eyes open for features of a problem that allow us to bypass the hard methods – yet we also need to learn those harder methods, because they are how most of life works!