(A new question of the week)
In an ellipse, \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) with focal distance c, parameters a, b, and c all make natural sense, and it is easy enough to see why \(a^2 = b^2 + c^2\). But in the hyperbola, \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\), the equivalent relationship, \(a^2 + b^2 = c^2\), is not nearly as natural, nor is the meaning of b itself; and many derivations of the formula skip over such details. We’ll dig in deeper here, using a mix of old Ask Dr. Math answers and new ideas.
Is there an intuitive proof?
I’ll start with the new question, from Ethan in mid-August:
Hey Math Doctors!
I was reviewing Conics when I noticed a strange step in a derivation of the equation of the hyperbola. Once you do a lot of algebra, you get c^2 x^2 − a^2 x^2 − a^2 y^2 = a^2 c^2 − a^4.You factor, and then get x^2 (c^2 − a^2 ) − a^2 y^2 = a^2 (c^2 − a^2 ). This is where I get confused. You need to set b^2 = c^2 – a^2. There is a similar relation for the ellipse, b^2 = a^2 – c^2, which is very intuitive. However, the hyperbola relation is bugging me. The proofs I’ve read through either rely on a picture or seem circular in the reasoning. Is there an intuitive proof for this relation without relying on the equation of hyperbola or relying on a picture “proof”? Also why does this relation look like the Pythagorean identity?
Here are links to the proofs I have read.
https://math.stackexchange.com/questions/3152904/can-this-equation-b2-c2-a2-be-derived-intuitively
I love your website!
Sincerely, Ethan
I looked through the references and saw mostly familiar material, similar to what we have said in the past; but none said what I had in my mind. I couldn’t recall whether I’d ever put my thoughts into written form. But this could be a chance to do so!
I answered:
Hi, Ethan.
This is a fun question, and I won’t be surprised if another of us has ideas to add. But I want to take a shot at it.
First, we need to clarify what you are hoping for. You ask for “an intuitive proof for this relation without relying on the equation of hyperbola or relying on a picture ‘proof’.”
I think we can provide an intuitive understanding, but it will not be an actual proof; and at some point we have to bring in the equation, because that’s where the idea of b comes from! And to me, nothing is intuitive if it doesn’t involve a picture!
As he’d mentioned, b commonly arises not from our initial geometric conception of the hyperbola, but “pops out of” the equation as we derive it, and is only then given meaning. But most derivations don’t actually relate the formula to its geometrical meaning. What we want to do is to make that connection between the equation and the picture, without merely declaring it to be so, which I think is what Ethan was seeing.
I looked through your links to see if any have the picture I have in mind, and the third one does; but it uses it within what you are perhaps finding too complicated a pile of algebra to be intuitive. I’ll probably be saying some of the same things, but hopefully in a context that will feel more natural.
I found (in my list of potential blog topics from the Ask Dr. Math archive) a typical derivation of the equation of the hyperbola here:
Deriving the Hyperbola Formula
(To read it, you’ll have to sign up for a free account with NCTM; they’ve hidden the site behind what I call a “freewall”.)
This is a warning I have to give these days, and is why links on our site have not yet been updated to give the new locations; without the explanation, people have assumed the link was bad. And when I say the site is “hidden”, I mean it: Though they changed from a “paywall” requiring membership, it is still impossible to search for archive pages, so the only way I can find them is if I have previously done so and put them on my list of future topics.
Our derivation of the formula
To make it easier for readers, I’ll insert that 1998 page in its entirety here:
Deriving the Hyperbola Formula When speaking of hyperbolas, why does: C squared = A squared + B squared? My entire math class, including my teacher, has tried to figure this out, but no one can come up with a logical reason. My teacher said that if we could come up with an explanation of this, we would get an A on our next test. Can you please help?
Doctor Jerry answered by deriving the equation of the hyperbola:
Hi Gauteaux, I wouldn't want to say that there is one reason everyone would accept, but here's a reason many would accept. A hyperbola can be defined as follows (ellipses have a similar definition): Two points, called foci, are given; they are 2c units apart. A hyperbola is the locus of all points for which the difference of the distances to the foci is a constant 2a, where 2a > 2c. To take a special case, suppose the two foci are at (-c,0) and (c,0). Then if (x,y) is on the ellipse, we must have: sqrt((x-c)^2 + y^2) - sqrt((x+c)^2 + y^2) = 2a This is the equation of one "branch." To keep things simple, I'll stick with this case. The other case is similar. This equation can be greatly simplified. First, write the equation as: sqrt((x-c)^2 + y^2) = sqrt((x+c)^2 + y^2) + 2a Square both sides and simplify. You will get: -c*x - a^2 = a*sqrt((x+c)^2 + y^2) Again, square both sides and simplify. You will get: (c^2 - a^2)x^2 - a^2*y^2 = a^2(c^2 - a^2) It is common to set c^2-a^2 = b^2, to simplify the equation. b^2*x^2 - a^2*y^2 = a^2*b^2 x^2/a^2 - y^2/b^2 = 1. Fortunately, the constant b is interesting. If you draw about the origin a rectangle that is 2a by 2b and then draw its diagonals, the diagonals are the asymptotes of the hyperbola. Please check my algebra. I can make mistakes.
You may recognize parts of this from Ethan’s description. I quoted this to give us a common starting point.
Other versions of the derivation, by Doctor Rob, can be found at
Focus of a Hyperbola First Principle Hyperbolas
Continuing my answer to Ethan,
As you’ve seen in other proofs, Dr. Jerry starts with the definition of the hyperbola:
Two points, called foci, are given; they are 2c units apart. A hyperbola is the locus of all points for which the difference of the distances to the foci is a constant 2a, where 2a < 2c.
So the hyperbola is defined in terms of a and c only. From this definition, we can also see (in the picture below) that the distance between the vertices will be 2a. The distance between vertices A and A’ is the difference between AF and AF’, since AF = A’F’.
Here’s a version of the picture containing only what we know to start with:
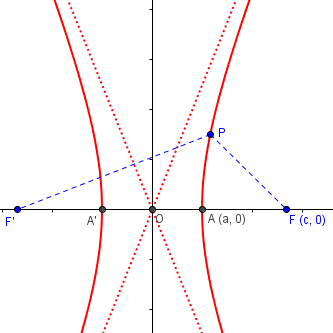
The hyperbola is the set of all points P such that \(|PF-PF’|=2a\). This includes the vertex, A, since \(|AA’|=|AF’-A’F’|=|AF’-AF|=2a\).
In the course of the work, he finds, as you said, that one expression occurs more than once, and says,
It is common to set c^2 – a^2 = b^2, to simplify the equation.
This is where many people feel it starts to feel circular! But we are just defining something called b here for convenience. At this point, it has no meaning in itself.
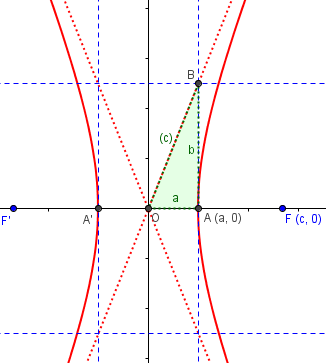
There is as yet no “b” in the picture! But whatever it is, that Pythagorean formula applies to it. And if we draw in such a triangle, we get this:
After finishing, he adds,
Fortunately, the constant b is interesting. If you draw about the origin a rectangle that is 2a by 2b and then draw its diagonals, the diagonals are the asymptotes of the hyperbola.
It can be shown easily from the equation that the diagonals are the asymptotes; when x and y are large, the equation becomes very close to x^2/a^2 + y^2/b^2 = 0, which is the equation of the asymptotes! The slopes of those lines are ±b/a.
Doctor Jerry didn’t prove his claim about the asymptotes; my claim is not quite a proof, but is intuitive. The larger x and y (and therefore both fractions on the left-hand side) get, the less difference the 1 on the right of the hyperbola’s equation matters, and it might as well be zero. Solve the resulting equation for y, and you get the equations of the two lines. We’ll see more on this later.
Why should that triangle involve c?
There is as yet no reason to think that OB should have length c, apart from the algebra. Does it make sense?
That’s the proof; my interest here is to think about why this result should be intuitively reasonable. So I’ll do a little hand-waving. (But there’s nothing up my sleeve!)
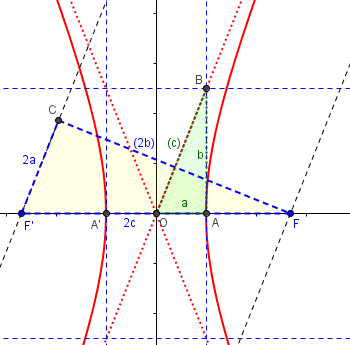
This is where I draw a picture:
The foci are F and F’; the vertices are A and A’; the hyperbola is in red, and its asymptotes are dotted red.
Values in parentheses are not initially known.
We aren’t going to assume what we found in the proof; in particular, we’ll define b not by the expression we stumbled across, but by placing point B on the asymptote, so that its slope is b/a.
The green triangle OAB has sides a, b, c; but what we wonder is, why would the hypotenuse be c? So I’m not declaring yet that it is; our goal is to show that. On the other hand, a and b are where they are by definition: a is defined as half the distance between the vertices, and b by the fact that b/a is the slope of the asymptote OB.
We’ll be seeing fuller proofs of the asymptote below. For now, we’re staying intuitive.
Now, suppose a point P is very far out on the hyperbola, approaching the asymptote. Segments FP and F’P will be nearly parallel to the asymptote, so they will approach the parallel lines I’ve drawn through F and F’. The definition of the hyperbola says that the difference between the distances FP and F’P is 2a; I’ve marked that as the length of F’C on the yellow triangle.
Can you see that the green and yellow triangles are similar (since they are right triangles with a common angle)?
Hypotenuse F’F has length 2c by definition; the similarity implies that OB/F’F = OA/F’C; that is, OB/(2c) = a/(2a). From that, it is obvious that OB = c. And that implies that c2 = a2 + b2.
Does that help?
So the yellow triangle is exactly twice the green one. And we can now fill in the “c” on the latter.
Incidentally, my picture also shows that b is the distance from a focus to an asymptote, which I’d never noticed until now!
Ethan replied, showing he’d put in the effort to fully understand:
This definitely helps! I had trouble understanding where F’C came from until I visualized sliding FP over and onto F’P; then, it was clear why F’C is 2a. Your picture looks similar to the picture in the link with the limit argument, but what helped was connecting b to the asymptote and showing the two similar right triangles.
Thank you for your help. I really appreciate it.
I responded:
To be honest, I was a little concerned that I hadn’t explicitly stated how I decided that F’C = 2a; that was essentially because some intuitions are easier seen than explained. I’m glad you got it; and perhaps giving you that little bit to work out for yourself helped the explanation work for you!
I’m not sure whether I’ve ever written up these ideas before, so I’m glad I had a chance to!
More from the archives
In preparing for this post, I discovered a 2019 answer containing links that were not in the list where I found Doctor Jerry’s explanation. Let’s look at those.
First, we have this question from 2007, nearly identical to Ethan’s except that it doesn’t ask for an intuitive explanation:
Meaning of Value of b in Hyperbola Equation I'm teaching conic sections, and I have been unable to find a justification for why in a hyperbola does a^2 + b^2 = c^2. You can easily justify a^2 = b^2 + c^2 in an ellipse by looking at special points. But I have yet to find a comparable explanation for hyperbolas. Textbooks just give you the formula and never explain where it comes from.
Doctor Fenton answered:
Hi Don,
Thanks for writing to Dr. Math. The relationship is true because that is the DEFINITION of b. b doesn't correspond to any geometric feature in the specification of the hyperbola, if you are using the description as the points whose distances to the two foci differ by a given amount. The foci are determined by the number c, and the given difference determines the coordinates of the vertices a, and with these two numbers, you can derive the equation
x^2 y^2
--- - --------- = 1
a^2 c^2 - a^2
(for a hyperbola centered at the origin, with foci (+/-c,0) and vertices (+/-a,0)). Since c^2 > a^2, c^2 - a^2 > 0, there is a positive number b such that b^2 = c^2 - a^2, and using this clearly simplifies the denominator of y^2 in the formula above. The point is that a and c are enough information to completely determine the hyperbola. No value of b is needed, and it is simply introduced to simplify the notation.
The details, of course, are in Doctor Jerry’s derivation.
Actually, the ellipse is similar: the foci and vertices (or the sum of the distances to the foci, which determines the vertices) are all that is needed to define the ellipse. It turns out that if you introduce the semi-minor axis b, you simplify the equation, and the quantity has a geometric meaning, but this was not part of the original specification.
The difference, of course, is that the semi-minor axis is visible in the graph of the ellipse; and Don’s “special points” form the right triangle we need:
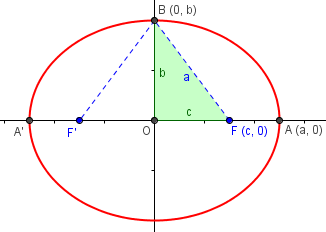
If we define point B as the co-vertex (an end of the minor axis, as the vertex A is an end of the major axis), then since it is a point on the ellipse, the sum \(BF+BF’ = 2a\), so \(BF=a\). This makes it clear that \(a^2 = b^2+c^2\). So although b is not used to derive the equation, its geometrical meaning is clear.
The hyperbola also has asymptotes y x y x - - - = 0 and - + - = 0 b a b a and these can be found by drawing a box with corners (+/-a,+/-b), but that box is not part of the original specification of the hyperbola. It is something you find after you have found the hyperbola. In both cases (ellipse and hyperbola), the definition essentially specifies a and c, and b is introduced for convenience. However, once you deduce the geometric significance of b, it offers an alternative way of specifying the conic. Any two of a, b, and c can be given and the third quantity determined. Does that help?
The equations for the asymptotes as given here are easy to derive from the form I previously gave, by factoring: $$\frac{x^2}{a^2}-\frac{y^2}{b^2}=0\;\Rightarrow\;\left(\frac{x}{a}-\frac{y}{b}\right)\left(\frac{x}{a}+\frac{y}{b}\right)=0$$
Proving the asymptotes
Finally, we have this 2011 question about asymptotes:
Approaching Asymptotes of Hyperbolas How do you derive the equations for the asymptotes of the standard hyperbolas? y = +/-(b/a)x y = +/-(a/b)x Solving for y, I got it down to: y = +/-(b/a) sqrt(x^2 - a^2) Then, letting x go to infinity, the a^2 is rendered insignificant, so y = +/-(b/a) sqrt((x^2)) This gives y = +/-(b/a)x But, how does this prove that y = +/- (b/a)x is an asymptote(s)? I need clarity here. I have been to site after site, and looked in books, and I still can't find an explanation. They all just state it and how to use it, but offer no proof. Could you help me with this?
(His second equation appears to be for a hyperbola with its major axis vertical, which he doesn’t otherwise mention.)
This time, we want a real proof. The trouble is that an asymptote like this is not quite the same as a limit (which would be a number, not a slanted line).
I answered:
Hi, Donald.
What you've done is a good informal demonstration of the idea; we can make it a little more convincing by saying it this way:
y = +/-b/a sqrt(x^2 - a^2)
= +/-b/a sqrt(x^2(1 - a^2/x^2))
When x is much larger than a, a^2/x^2 is much less than 1, so this will be very close to
y = +/-b/a sqrt(x^2) = +/-(b/a)x
This is much like what I did above.
For a real proof, we have to start with the definition of "asymptote"; without that, no proof is possible, since we wouldn't know what we were trying to prove!
An asymptote is a line that is approached more and more nearly by the curve as x increases. That is, if we have a curve y = f(x) and a line y = mx + b, the latter is an asymptote of the former if
lim[x->oo](f(x) - (mx + b)) = 0
To show that y = bx/a is an asymptote of y = b/a sqrt(x^2 - a^2), we want to show that
lim[x->oo](b/a sqrt(x^2 - a^2) - bx/a) = 0
Is it?
lim[x->oo](b/a sqrt(x^2 - a^2) - bx/a)
= lim[x->oo](b/a (sqrt(x^2 - a^2) - x))
= b/a lim[x->oo](sqrt(x^2 - a^2) - x)
(sqrt(x^2 - a^2) - x)(sqrt(x^2 - a^2) + x)
= b/a lim[x->oo]--------------------------------------------
(sqrt(x^2 - a^2) + x)
(x^2 - a^2) - x^2
= b/a lim[x->oo]---------------------
sqrt(x^2 - a^2) + x
-a^2
= b/a lim[x->oo]--------------------------
x sqrt(1 - a^2/x^2) + x
-a^2
= b/a lim[x->oo]--------------------------
x(sqrt(1 - a^2/x^2) + 1)
-a^2*1/x
= b/a lim[x->oo]-----------------------
sqrt(1 - a^2/x^2) + 1
-a^2(0)
= b/a lim[x->oo]-------------
sqrt(1) + 1
0
= ---
2
= 0
So the curve does in fact approach the line.
I’ve corrected some serious typos here.
The form used here for the asymptotes, \(y=\pm\frac{b}{a}x\), is the slope-intercept form. Putting everything on one side yields the form Doctor Fenton used above: $$y=\pm\frac{b}{a}x\\ \\ \frac{b}{a}x\pm y=0\\ \\ \frac{1}{b}\cdot \frac{b}{a}x\pm \frac{1}{b}\cdot y=\frac{1}{b}\cdot 0\\ \\ \frac{x}{a}\pm \frac{y}{b}=0$$

Pingback: Degenerate Conics I: Mystery of the Missing Case – The Math Doctors
I appreciate your explanations above, but I decided to keep digging and I found a relatively easy geometric explanation of the Pythagorean theorem for the hyperbola. First, construct a circle whose center is the same as the hyperbola with a radius equal to c. Next, inscribe a rectangle with length 2a (so it passes through the vertices). Label the width of the rectangle as 2b. A segment from the center to a corner of the rectangle has length of c, and forms a right triangle with legs of length a and b. I demonstrated this to my high school students using graphing software and it seemed to go over well.
PS I used to live in Rochester and taught at RIT for a while. Wish I had known about your website back then. It would have been fun to collaborate!
Hi, Tim.
Yes; what you are describing is the second picture in the post, except that I didn’t show the circle. That picture provides a meaning for the formula, and makes it memorable, while providing an easy way to construct the asymptotes (whether you know a and c, or a and b). But I wouldn’t call it an explanation of why this formula is true. It’s more a demonstration.
Hi, Doctors
I tried to find some equations of parabola for my presentation in the topic hyperbola itself so I need a help to justify the relationship between a,b and c could you help me regarding this?
Hi, Sam.
You said, “I tried to find some equations of parabola for my presentation in the topic hyperbola itself.”
Are you asking about the hyperbola, or the parabola? Assuming the former, what about this post is insufficient? And if you meant what you said, and are talking about equations for the parabola, what are a, b, and c there?
Please don’t reply here, but through our Ask a Question link, which is where specific questions like this belong.
This is an amazing article! I spent hours searching for a good explanation on this but most websites do not offer a satisfactory discussion into this topic (which i’m sure frustrates many students). Thank you for the work that is being done here!