(A new question of the week)
I had a long discussion recently about the Cartesian product of sets, answering questions like, “How is it Cartesian?” and “How is it a product?” I like discussions about the relationships between different concepts, and people who ask these little-but-big questions. We’ll be looking at about a quarter of this conversation, including the origin of the concept and what it really means (and doesn’t mean).
Cartesian product and Cartesian coordinates
The question came in late August from Shaurya, whose question about sets we examined three weeks ago:
Respected maths doctors
Today I have started my new chapter in mathematics, that is relations and functions, and the first subtopic of this chapter is the Cartesian product of sets.
When I read this name only, the Cartesian product of sets, I got too much surprised because here we are all talking about sets and relations and functions, then why the multiplication of the two sets A and B that is A×B is named Cartesian products of sets? Does it have something to do with co-ordinate geometry?
Please explain me why this multiplication of two sets A and B is named Cartesian product of sets. I have tried too much to relate it with co-ordinate geometry but cannot come to the final result that is it named the Cartesian product of sets due to some convention or named arbitrarily, or because it shares some properties with the co-ordinate geometry?
Thank you
Shaurya has previously learned about the Cartesian plane, also called the rectangular coordinate plane, in which each point is associated with an ordered pair \((x,y)\). He is now learning about the Cartesian product of two sets, which is defined as \(A\times B = \{(a, b) : a\in A, b\in B\}\). That is, it is the set of all ordered pairs (a, b) where a is an element of set A, and b is an element of set B. So his first question is about the name, Cartesian. Are the two concepts related?
How René Descartes is related to both
I answered, starting with the name itself:
Hi, Shaurya.
Yes, this name is closely related to the Cartesian coordinate system.
According to Wikipedia,
The Cartesian product is named after René Descartes, whose formulation of analytic geometry gave rise to the concept, which is further generalized in terms of direct product.
The path from Descartes’ own work to Cartesian coordinates, and then to the Cartesian product of sets, was long; he never actually used the \((x, y)\) coordinates that are named for him:
But the relationship is not quite direct, as Descartes himself did not see things in nearly the modern way. According to Earliest Known Uses of Some of the Words of Mathematics,
CARTESIAN, from Cartesius the Latin name for the mathematician and philosopher René Descartes (1596-1650), appears in several expressions. The mathematical ones usually relate to La Géométrie (1637). The terms can be misleading, for as Boyer remarks:
Cartesian geometry now is synonymous with analytic geometry, but the fundamental purpose of Descartes was far removed from that of modern textbooks. The theme is set by the opening sentence: “Any problem in geometry can easily be reduced to such terms that a knowledge of the lengths of certain lines is sufficient for its construction.” As this statement indicates, the goal is generally a geometric construction, and not necessarily the reduction of geometry to algebra. The work of Descartes far too often is described simply as the application of algebra to geometry, whereas actually it could be characterized equally well as the translation of the algebraic operations into the language of geometry.
This quotation is taken from the 1968 edition of A History of Mathematics, pages 370-371.
…
Cartesian product. This set theoretic term entered circulation in the 1930s. Previously product (Produkt) was the established term: see, e.g. Felix Hausdorff Grundzüge der Mengenlehre (1914, p. 37)) Kuratowski wrote produit for intersection and produit cartésien for the former product (Topologie I (1934, p. 7)). Hausdorff had used Durchschnitt for intersection, so there was no danger of confusion. …
Boyer (p. 346) considers the term “Cartesian product” an anachronism because Descartes did not think of his coordinates as number pairs.
The first entry here emphasizes the distance between Descartes’ work and both concepts we now call “Cartesian”; more on that below.
The second entry shows that the concept of Cartesian product came about 300 years after Descartes, and was initially just called a “product”. His name was added to distinguish this from the intersection of sets (which can be thought of as a product; in fact the related logical “and” is written as multiplication in Boolean algebra, and the probability of the intersection of events is found by multiplying).
I continued:
The Cartesian coordinate system as we know it today, in which any point in the plane is identified with an ordered pair (x, y), developed from Descartes’ geometrical ideas, and in turn led to the generalized idea of forming the “product” of any two sets as the set of ordered pairs from the sets.
In particular, the Cartesian product R×R = R2 of the real number line with itself is the Cartesian plane.
Descartes’ idea led to identifying points as ordered pairs of real numbers, so that what we call the Cartesian plane is in fact the Cartesian product of two sets of real numbers. The latter is a generalization of the former.
Descartes just planted a seed
Later in the conversation, we came back to the question of what Descartes actually did. Here is what I said in answer to a question about the Boyer quote above:
Descartes was not doing what we are doing when we use x and y to describe something. That’s what Boyer is saying. Let’s look more deeply into what he actually did.
First, the book in which he introduced these ideas is La Géométrie. The Wikipedia article about that says,
Descartes is often credited with inventing the coordinate plane because he had the relevant concepts in his book; however, nowhere in La Géométrie does the modern rectangular coordinate system appear. This and other improvements were added by mathematicians who took it upon themselves to clarify and explain Descartes’ work.
He did use x and y; but did not use the axes, and did not measure them perpendicularly.
The Wikipedia article on the Cartesian coordinate system says,
The adjective Cartesian refers to the French mathematician and philosopher René Descartes, who published this idea in 1637. It was independently discovered by Pierre de Fermat, who also worked in three dimensions, although Fermat did not publish the discovery. The French cleric Nicole Oresme used constructions similar to Cartesian coordinates well before the time of Descartes and Fermat.
Both Descartes and Fermat used a single axis in their treatments and have a variable length measured in reference to this axis. The concept of using a pair of axes was introduced later, after Descartes’ La Géométrie was translated into Latin in 1649 by Frans van Schooten and his students. These commentators introduced several concepts while trying to clarify the ideas contained in Descartes’ work.
I found this article about what he did in this book; I haven’t read much of it, but just skimming through it, you can see that the way in which he used algebra to solve geometric problems involved no ordered pairs or axes, and the “coordinates” that he does use involve no right angles.
In general, his work looks more like what we do today when we label a geometrical figure with variables, than like our analytic geometry.
Here is another article, perhaps simpler. You don’t find any axes or ordered pairs here. What you do find are the x and y shown here:
That is as close as he comes to our (x, y). He planted the seed out of which the ideas of analytic geometry, the Cartesian plane, and later the Cartesian product, grew; but a seed looks very different from a fully-grown plant!
Of course, the important fact for Shaurya’s original question is simply that both concepts grew from that Cartesian seed.
The Cartesian plane as a Cartesian product
Going back to my initial response, Shaurya was not yet clear on the relationship of the two concepts:
I am not able to deduce the final result; please help me. What is meant by saying that Cartesian product R×R=R2 of the real number line with itself is the Cartesian plane.
I replied:
If you are studying the Cartesian product, then you either have seen this, or soon will. This should not surprise you, though it is quite possible that you are being introduced to the concept with only finite sets as examples.
As I think you know, if we have two sets A and B, their Cartesian product is defined as A×B = {(x, y) : x ∈ A, y ∈ B}.
So R×R is the Cartesian product {(x, y) : x, y ∈ R}. We also call this R2, because that is how we write the product of something with itself, though you may not have seen this notation yet. And the concept of the Cartesian (coordinate) plane is precisely that every point of the plane corresponds to an ordered pair (x, y) of real numbers.
I think you just need to be patient and study the chapter you are in, which will probably answer your questions. They introduce the Cartesian product before defining relations, because a relation is defined as a subset of a Cartesian product; it is a set of ordered pairs.
The Cartesian product as a product
Shaurya answered, struggling to make sense of the word “product”, working from a wrong meaning of the Cartesian product to an attempted explanation for the name:
Let me try to explain my problem.
In your previous reply you have mentioned that R×R = R2. It might be possible that I am interpreting it wrong but I am interpreting R×R = {(R, R)}. So please tell me is R2 = {(R, R)} and if so how.
When we talk about Cartesian product, we are taking two sets, say A = {2}, B = {4}, and for multiplying these two sets we are putting a Saint Andrew cross (×) between these two sets in a particular order, say A×B = {2}×{4} so what I also think is that the results should be equal to {8}. But it is not happening as such.
Why is the thing that is happening here is that the result is coming as 2 and 4 and they are in curved brackets and there is, between 2 and 4 that would provide a final result as (2, 4). And also the multiplication of the sets is not following the commutative property as followed by the normal multiplication of the two sets. So why is this procedure considered a product when it is not same as the product of two simple numbers?
But yes one pattern that I found was that it the two sets are multiplied with each other by following the distributive property. For this let us consider two sets A = {1, 2}, B = {3, 4, 5} so I deduce its multiplication as follows A×B = 1×{3, 4, 5}, 2×{3, 4, 5} = {(1, 3), (1, 4), (1, 5), (2, 3), (2, 4), (2, 5)} this have something similar as deducing the product of real numbers by using distributive property example in (5 + √7)(2 + √5) = 5(2 + √5)√7(2 + √5) = 10 + 5√5 + 2√7 + √35 show procedure of the curve taking out cartesian product is considered as the product of two sets because it is following the distributive property in the similar way as followed by the multiplication of the real numbers or the clue behind calling them as the product is hidden behind that we are not multiplying here the numbers directly but the two sets for example in sets {2}×{4} we are not multiplying simply like 2×4 that is twoness × fourness but the two sets only.
Shaurya sees that we aren’t multiplying numbers (like 2 and 4), but is trying to find a relationship between what a Cartesian product actually is (each element of A paired with each element of B) and multiplication of numbers. He is being very creative!
In particular, he sees that \(\{2\}\times\{4\}=\{(2,4)\}\), while \(\{4\}\times\{2\}=\{(4,2)\}\), so this operation is not commutative. On the other hand, he sees a connection with the distributive property, and proposes this as a reason for the name.
I answered:
Now I realize that your question about the name “Cartesian product” was not just about the name “Cartesian”, as I had thought, but about the use of the word “product“. You appear to have some incorrect expectations, but have found some interesting ways to correct them.
This is genuinely commendable, even though his specific ideas are wrong, as we’ll see. Too many students, when they find a new idea not fitting into their existing framework, just accept it blindly, often because they don’t expect math to make sense! Shaurya does expect sense, and tries to manufacture it.
So what is the relationship to multiplication of numbers?
First, you need to understand that this operation is not an extension of multiplication of real numbers, but is called multiplication (and denoted by a multiplication symbol) by analogy. It should not be expected to follow all the properties of multiplication. You may find it interesting to read this:
What is Multiplication … Really?
This doesn’t mention the Cartesian product, but some similar things can be said about it. One thing it mentions, though, is that operations we call multiplication are not always commutative.
This would have been an excellent example for that post!
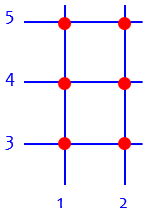
I think the main reason this is called a product is that it multiplies the cardinalities (sizes) of the two sets. Taking your example, {1, 2} × {3, 4, 5} = {(1, 3), (1, 4), (1, 5), (2, 3), (2, 4), (2, 5)}, and the cardinalities are respectively 2, 3 and 6: 2 × 3 = 6.
This corresponds to the idea of making an array of 2 rows of 3 objects, which is the elementary model of what multiplication does (for whole numbers). It’s also interesting that if we interchange the factors and multiply {3, 4, 5} × {1, 2}, although the new product is not the same as the first, it does have the same cardinality. (This is the elementary justification for the commutative property of multiplication of whole numbers.)
Here is a common way to represent \(\{1, 2\} \times \{3, 4, 5\}\), showing that \(2\times 3=6\); each dot represents an ordered pair:
But there are some significant errors in what you say here.
First, and simplest, it is not true that R × R = {(R, R)}. The latter is a single ordered pair of two sets, not the set of all ordered pairs taken from two sets, which is the Cartesian product.
You have, I think, understood that the Cartesian product does not involve products of elements (as in your example, where {2} × {4} = {2, 4)}, not {8}). That was simply a wrong expectation on your part. We define this operation in its own way, and you must follow the definition, not your own preconceptions. And your expectation that any product would be commutative is wrong; again, the properties of this operation are determined from its definition.
This is explained in the post I referred to.
But you are wrong in thinking that the definition arises from the distributive property. It’s an interesting idea, which I don’t think I’d ever considered, to observe that
{1, 2} × {3, 4, 5} = {{1} × {3, 4, 5}, {2} × {3, 4, 5}} = {(1, 3), (1, 4), (1, 5), (2, 3), (2, 4), (2, 5)}.
But technically, this is not really true, as the second expression is actually a set containing two sets of 3 elements, namely
{{(1, 3), (1, 4), (1, 5)}, {(2, 3), (2, 4), (2, 5)}}
This is not the same as the third expression, which contains 6 sets.
Also, this is not really distribution, as there is no addition involved. So while this is very similar to distribution (combining each element of one set with each element of the other, as distribution multiplies each addend in one expression by each addend in another), it is not what distribution would really mean.
So the Cartesian product is similar to distribution, but not identical to it. But this does raise a further question:
Now, since, in my post I referred to above, I suggest that the distributive property is almost a defining property of multiplication, I have to ask myself, does the Cartesian product have such a property? If so, what would we use for “addition”, since you can’t add sets?
It turns out that, in fact, the Cartesian product distributes over several set operations, as mentioned in Wikipedia:
Here are some rules demonstrating distributivity with other operators:
\(A\times(B\cap C)=(A\times B)\cap (A\times C)\)
\(A\times(B\cup C)=(A\times B)\cup (A\times C)\)
\(A\times(B\setminus C)=(A\times B)\setminus (A\times C)\)
…
Commonly, we think of the union as the equivalent of addition in set theory (and more so in probability and logic), so that is what I would use. But even this is quite different from your idea of distribution. An example would be, if A = {1, 2}, B = {2, 3, 4}, and C = {3, 4, 5}, that
A × (B ∪ C) = {1, 2} × {2, 3, 4, 5}
= {(1, 2), (1, 3), (1, 4), (1, 5), (2, 2), (2, 3), (2, 4), (2, 5)}
(A × B) ∪ (A × C)
= {(1, 2), (1, 3), (1, 4), (2, 2), (2, 3), (2, 4)} ∪ {(1, 3), (1, 4), (1, 5), (2, 3), (2, 4), (2, 5)}
= {(1, 2), (1, 3), (1, 4), (1, 5), (2, 2), (2, 3), (2, 4), (2, 5)}
which are the same.
So the Cartesian product does have the property that I have said distinguishes multiplication from other operations.
So, yes, the Cartesian product does have a distributive property; but that has nothing to do with your idea of using distribution. Yet your idea is a nice way to think of this product.
I’ve probably said far too much, but I hope some of this helps!