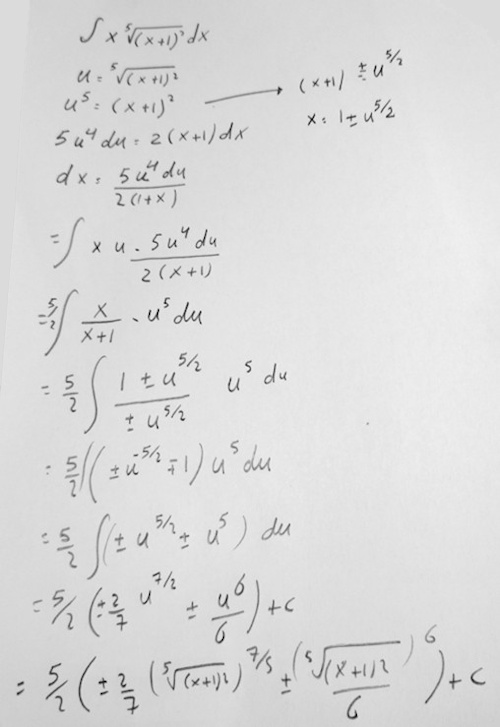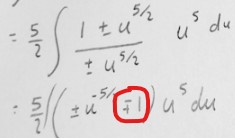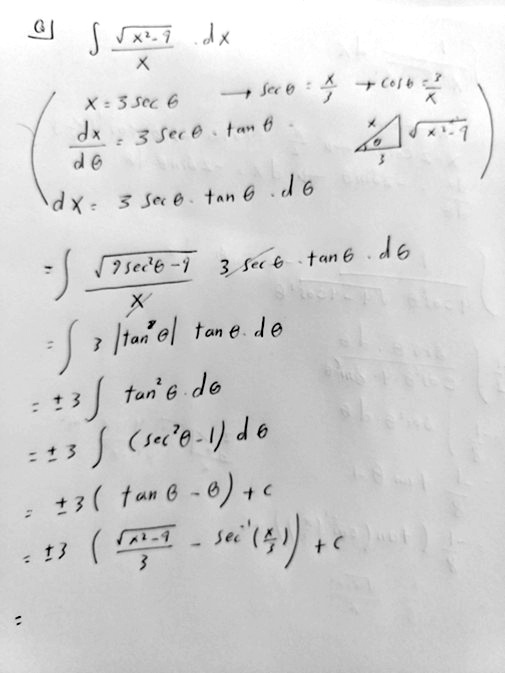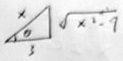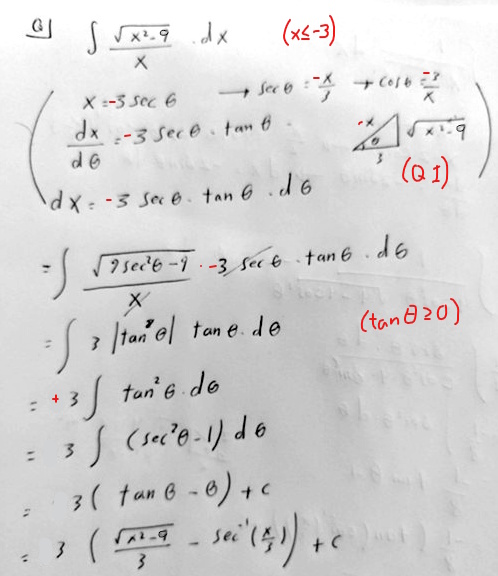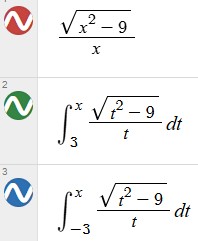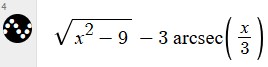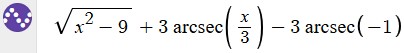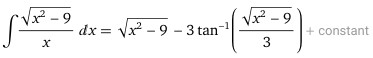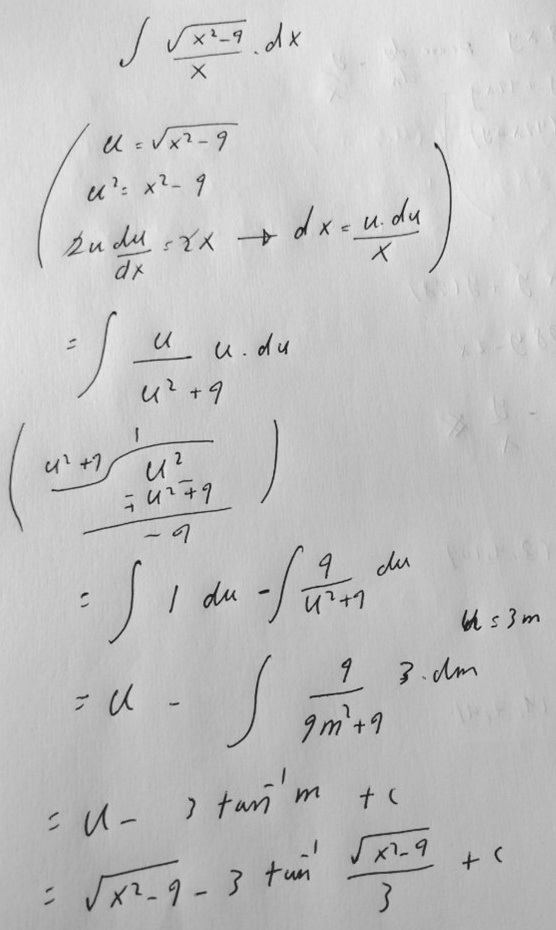A couple recent questions about integration turn out to be related to our last couple posts, in which we discussed substitutions that are not one-to-one. It’s better disguised here (and isn’t intertwined with symmetry issues!). You’ll also see a couple errors I made in correcting the student’s errors, which I am not hiding because you can learn a lot from mistakes!
A u-substitution with a twist
First, from Amia in November:
Hi Dr Math,
I want to check the solution for the question below.
Thank you in advance
Amia has used a substitution, letting \(u=\sqrt[5]{(x+1)^2}=(x+1)^{2/5}\). This results in some plus-or-minus symbols, which are problematic. On the other hand, most students probably wouldn’t have noticed the sign issue at all!
(If you happen to notice an easier way to solve this, we’ll get there! For now, we’re focused on fixing his method.)
But there are several errors here, which we first have to deal with. I answered:
Hi, Amia.
There’s an error near the start, where you wrote 1 instead of -1.
But then what happened here?
Beyond that, I would just simplify a little more; also, I’m not happy with an answer containing ±. I’d have done this work in terms of two specific cases, one where “+” is appropriate, and another where it’s “-“. I may want to think a little more about how this is best handled.
The first bit arose from solving \(x+1=\pm u^{5/2}\), so it should be \(x={\color{Red}{-}}1\pm u^{5/2}\). The second arose from dividing ± by ±, which are synchronized so that they will always be the same sign, so it should just be +. And I could have said something much stronger than “not happy”! The answer must be a function, so we’ll have to have only one sign at a time, much as we had to split a definite integral into two parts last time.
Correcting the work
We never got a reply, but the ideas here will be important when we move to the next question; so let’s make the corrections, and then think about the sign issue. Here is the work, corrected except for the plus-or-minus:
$$\int x\sqrt[5]{(x+1)^2}dx\\u=\sqrt[5]{(x+1)^2}\\u^5=(x+1)^2\\x=-1\pm u^{5/2}\\5u^4du=2(x+1)dx\\dx=\frac{5u^4du}{2(x+1)}=\frac{5u^4du}{\pm2u^{5/2}}=\pm\frac{5}{2}u^{3/2}du$$
Here we’ve set up the substitution. I personally prefer never to have both variables (x and u) together in an integral, as Amia did, so here I first wrote dx in terms of u alone, and in the next line I will immediately replace both x and dx with the expressions we have, and the radical with u.
We need to deal properly with the \(\pm\) introduced here, which came about because we’re taking a square root in solving for x; the problem is that we have defined u as a function of x that is not one-to-one, so there are two possible values for x. They are not both used at once; each actually applies in a different case. In particular, the top sign (here +) applies when \(x\ge-1\), and the bottom sign (here -) applies when \(x<-1\). Note also that u is non-negative.
Above, I corrected the first explicit sign error I mentioned. Continuing,
$$\int x\sqrt[5]{(x+1)^2}dx\\=\int \underset{x}{\underbrace{\left(\pm u^{5/2}-1\right)}}\underset{\sqrt[5]{(x+1)^2}}{\underbrace{\cdot u\cdot\vphantom{\Big]}}}\;\underset{dx}{\underbrace{\pm\frac{5}{2}u^{3/2}du}}\\=\frac{5}{2}\int\left(u^5\mp u^{5/2}\right)du$$
There I corrected the second sign error. Now we’ll integrate:
$$=\frac{5}{2}\left(\frac{1}{6}u^6\mp\frac{2}{7}u^{7/2}\right)\\=\frac{5}{12}u^6\mp\frac{5}{7}u^{7/2}$$
Now we have to return to the original variable, then simplify:
$$=\frac{5}{12}\left(\sqrt[5]{(x+1)^2}\right)^6\mp\frac{5}{7}\left(\sqrt[5]{(x+1)^2}\right)^{7/2}\\=\frac{5}{12}(x+1)^{12/5}\mp\frac{5}{7}(x+1)^{7/5}\\=\frac{35}{84}(x+1)(x+1)^{7/5}\mp\frac{60}{84}(x+1)^{7/5}\\=\frac{5}{84}\left(7(x+1)\mp12\right)(x+1)^{7/5}\\=\frac{5}{84}\left(7x+7\mp12\right)(x+1)^{7/5}\\=\frac{5}{84}\left(7x+19\right)(x+1)^{7/5}\text{ or }\frac{5}{84}\left(7x-5\right)(x+1)^{7/5}$$
I chose to factor out the common radical, which is the most complicated part of the expression.
As a final answer, we should write the two cases as a piecewise function, using the top sign for the case \(x\ge-1\):
$$\cases{\frac{5}{84}\left(7x+19\right)(x+1)^{7/5}& if $x\lt-1$\\
\frac{5}{84}\left(7x-5\right)(x+1)^{7/5}& if $x\ge-1$}$$
Note, however, that technically each of these will have its own arbitrary constant; since the combined function needs to be continuous, we have to check that we don’t have to add a constant to one piece to make it so. (We don’t, because both are zero at the “seam”.)
We could have split the interval at the start and done all the work separately for each case; but since it is the same work apart from which sign we use, what we did here is easier and clearer.
Correcting the correction
But this is wrong! I’ve made a very subtle error here, which I didn’t notice until I checked the answers several ways; so I think it’s worth showing.
In replacing $$\left(\sqrt[5]{(x+1)^{2/5}}\right)^{7/2}=\left((x+1)^2\right)^{7/2}$$ with $$(x+1)^{7/5},$$ I lost the fact that the square root is always positive; the reality is that \(\left(a^2\right)^{1/2}=|a|\), not just \(a\). So we should have \(|x+1|^{7/5}\). But that’s just \(\pm(x+1)^{7/5}\), with the top sign when \(x\ge-1\), which will cancel out the sign change.
So the correct work looks like this:
$$\frac{5}{12}\left(\sqrt[5]{(x+1)^2}\right)^6\mp\frac{5}{7}\left(\sqrt[5]{(x+1)^2}\right)^{7/2}\\=\frac{5}{12}(x+1)^{12/5}\mp\frac{5}{7}|x+1|^{7/5}\\=\frac{5}{12}(x+1)^{12/5}\mp\pm\frac{5}{7}(x+1)^{7/5}\\=\frac{35}{84}(x+1)(x+1)^{7/5}-\frac{60}{84}(x+1)^{7/5}\\=\frac{5}{84}\left(7(x+1)-12\right)(x+1)^{7/5}\\=\frac{5}{84}\left(7x+7-12\right)(x+1)^{7/5}\\=\frac{5}{84}\left(7x-5\right)(x+1)^{7/5}$$
There is really only one case. And it probably would have been safer to explicitly work with each case separately, so we wouldn’t lose sight of signs in the midst of the work!
A definite integral
Now, if we were doing a definite integral, we could have split the integral itself into two parts, each using a different inverse in the work.
Suppose, for example, we wanted to integrate from \(-3\) to \(3\). We would split at \(-1\):
$$\int_{-3}^3x\sqrt[5]{(x+1)^2}dx=\int_{-3}^{-1}x\sqrt[5]{(x+1)^2}dx+\int_{-1}^3x\sqrt[5]{(x+1)^2}dx$$
The first integral becomes
$$\int_{-3}^{-1}x\sqrt[5]{(x+1)^2}dx=\int_{\sqrt[5]{4}}^{0}\left(-u^{5/2}-1\right)u\left(-\frac{5}{2}u^{3/2}du\right)\\u=\sqrt[5]{(x+1)^2}\\x=-u^{5/2}-1\\x=-3\rightarrow u=\sqrt[5]{4}\\x=-1\rightarrow u=0\\dx=-\frac{5}{2}u^{3/2}du$$
$$\dots=\frac{5}{2}\int_{\sqrt[5]{4}}^{0}\left(u^5+u^{5/2}\right)du=\frac{5}{2}\left[\frac{1}{6}u^6+\frac{2}{7}u^{7/2}\right]_{\sqrt[5]{4}}^{0}\\=-\frac{5}{12}2^{12/5}-\frac{5}{7}2^{7/5}=-\frac{5}{3}2^{2/5}-\frac{10}{7}2^{2/5}=-\frac{65}{21}2^{2/5}$$
The second becomes
$$\int_{-1}^{3}x\sqrt[5]{(x+1)^2}dx=\int_{0}^{\sqrt[5]{16}}\left(u^{5/2}-1\right)u\left(\frac{5}{2}u^{3/2}du\right)\\u=\sqrt[5]{(x+1)^2}\\x=u^{5/2}-1\\x=-1\rightarrow u=0\\x=3\rightarrow u=\sqrt[5]{16}\\dx=\frac{5}{2}u^{3/2}du$$
$$\dots=\frac{5}{2}\int_{0}^{\sqrt[5]{16}}\left(u^5-u^{5/2}\right)du=\frac{5}{2}\left[\frac{1}{6}u^6-\frac{2}{7}u^{7/2}\right]_{0}^{\sqrt[5]{16}}\\=\frac{5}{12}2^{24/5}-\frac{5}{7}2^{14/5}=\frac{20}{3}2^{4/5}-\frac{20}{7}2^{4/5}=\frac{80}{21}2^{4/5}$$
Adding, we get $$\frac{80}{21}2^{4/5}-\frac{65}{21}2^{2/5}\approx2.5486$$
Note that we never had to worry about that subtle error involving signs. It’s easier to handle signs when you work with specific numbers!
If we instead used our indefinite integral, we would get
$$\frac{5}{84}\left(7x-5\right)(x+1)^{7/5}\Big|_{-3}^3=\frac{5}{84}\left(16\right)(4)^{7/5}-\frac{5}{84}\left(-26\right)(-2)^{7/5}\\=\frac{20}{21}\left(4^{7/5}\right)-\frac{65}{42}\left(2^{7/5}\right)=\frac{80}{21}2^{4/5}-\frac{65}{21}2^{2/5}\approx2.5486$$
That’s good.
A much easier substitution
When I try a substitution, I try to keep in mind that it might not turn out to be the best choice, so I am willing to consider alternatives if I run into difficulty. So at some point I would probably have asked, is there another substitution to try?
Here, a natural choice is the “inner function”, which is just \(x+1\). Let’s try that:
$$\int x\sqrt[5]{(x+1)^2}dx\\u=x+1\\x=u-1\\dx=du$$
$$=\int\underset{x}{\underbrace{\left(u-1\right)}}\underset{\sqrt[5]{(x+1)^2}}{\underbrace{u^{2/5}\vphantom{]}}}\;\underset{dx}{\underbrace{\vphantom{]}du}}=\int\left(u^{7/5}-u^{2/5}\right)du\\=\frac{5}{12}u^{12/5}-\frac{5}{7}u^{7/5}=\frac{5}{12}(x+1)^{12/5}-\frac{5}{7}(x+1)^{7/5}\\=\frac{35}{84}(x+1)(x+1)^{7/5}-\frac{60}{84}(x+1)^{7/5}\\=\frac{5}{84}\left(7(x+1)-12\right)(x+1)^{7/5}\\=\frac{5}{84}\left(7x-5\right)(x+1)^{7/5}$$
This substitution is one-to-one, and the work was straightforward. A definite integral is similarly simple:
$$\int_{-3}^3x\sqrt[5]{(x+1)^2}dx=\int_{-2}^4\left(u^{7/5}-u^{2/5}\right)du=\left[\frac{5}{12}u^{12/5}-\frac{5}{7}u^{7/5}\right]_{-2}^4\\=\frac{5}{84}\left[\left(7u-12\right)u^{7/5}\right]_{-2}^4=\frac{5}{84}\left[\left(16\right)4^{7/5}\right]-\frac{5}{84}\left[\left(-26\right)(-2)^{7/5}\right]\\=\frac{5}{84}\left[\left(64\right)2^{4/5}-\left(52\right)2^{2/5}\right]=\frac{80}{21}2^{4/5}-\frac{65}{21}2^{2/5}\approx2.5486$$
Just as before.
A trig-substitution with a similar twist
Two weeks later, Amia asked about another integration:
Hi Dr math,
I want to check the solution for the question below.
And I have a question: I see many solutions for similar questions doesn’t consider the double sign, Shall I consider the angle is acute??
Thank you in advance.
This time we have a trig substitution, rather than a u-substitution; as I’ve mentioned recently, this requires an explicit inverse function at some point, and, as he points out, I have too often seen sign issues ignored in such cases. Again, Amia is creditably aware of the issue, but has not quite gone far enough in handling it!
The secant substitution is the trickiest trig substitution; I checked the book most of my students use, and it carefully points out the sign issues we’ll be dealing with. But students often don’t pay enough attention …
I answered, pointing this out:
Hi, Amia. I can think of several directions to go in discussing this, so we may have more to say after my initial thoughts.
The first thing to say is that your answer can’t be considered correct, because an indefinite integral has to be a function; it can’t have two values.
So if your idea is valid at all, then you need to specify for what values of x the sign should be negative — that is, make this a piecewise function.
The second thing is that you are entirely right in being concerned about this issue of signs in substitutions. I think it came up in a recent discussion, but you didn’t choose to pursue it. We need to do so here.
That discussion was, of course, the question above, which I have now pursued! It will look just a little different here.
We need two cases
Now, looking at the details, everything until you introduce the ± sign looks good, except for one detail:
Do you notice that the picture assumes that x > 0? The two legs of such a triangle can be negative in some quadrants, but the hypotenuse is always taken to be positive! Often these pictures assuming the first quadrant work out correctly, but we should always consider other cases. But here, I’m not even sure how I’d draw the picture if x < 0.
So the first thing to do will be to separately consider two cases, according to whether x is positive or negative.
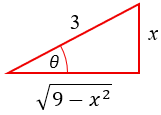
If the substitution had been \(x=3\sin\theta\), I would have drawn my triangle in the first quadrant,
and at least imagined drawing another in the fourth quadrant, for the case when x is negative:
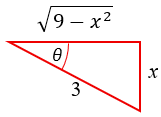
These would be the only two cases, because I would be explicitly stating the inverse, \(\theta=\arcsin\left(\frac{x}{3}\right)\), whose range is from \(-\frac{\pi}{2}\) to \(\frac{\pi}{2}\). And the cosine is always positive, so the square root is appropriate.
If I happened to use \(x=3\cos\theta\), which is rarer, I would have drawn my triangles in the first and second quadrants, representing the range of \(\theta=\arccos\left(\frac{x}{3}\right)\).
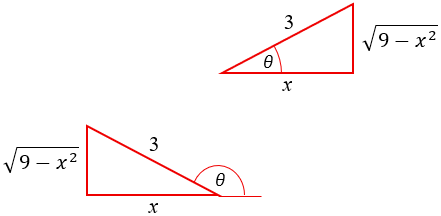
And here the sine is always positive, so the square root again causes no trouble.
But here we are using \(x=3\sec\theta\), and x is the hypotenuse, which is always positive! So how can we handle that negative case? We’ll get there.
Another, somewhat related, issue that is often overlooked is that in trig substitutions, we really need to specify the inverse substitution. You state that x = 3 sec(θ); but this is not a one-to-one function, and when you eventually make the reverse substitution, you assume that θ = arcsec(x/3), which is not the only possible value for θ. I consider it important to specify this from the start, so that the full meaning of the substitution is clear. This determines the domain of θ, namely 0 ≤ θ < π/2, π/2 < θ ≤ π. So we’re in the first or second quadrant. (But see Ranges of Inverse Trig Functions for a subtle issue that could arise, depending on your textbook.)
Thinking about the inverse function from the start can ensure that we think about ranges, and hopefully see whether we need separate cases or not.
We needed two cases anyway!
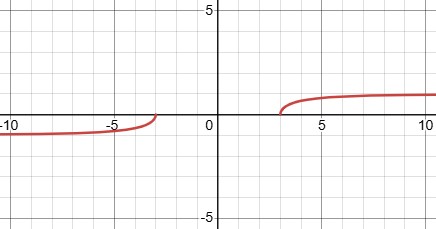
But there’s something else I thought about after this observation: What is the domain of the integrand? And how will that affect the integral? Here is a graph of the integrand:
So the integral will consist of two separate functions, on non-adjacent domains. So it makes good sense, in the first place, to work out the integral in two cases.
Of course, the domain is where \(x^2-9\ge0\), which means \(|x|\ge3\). We didn’t need to see the graph to know this – but it’s an easy fact to miss, if you don’t make a habit of checking domains whenever you see a function.
When the domain of the integrand comes in separate pieces, the integral will as well; in fact, it might involve different constants in the two parts (as we’ll be seeing). So piecewise functions are an inherent part of the problem, not just an artifact of our substitution.
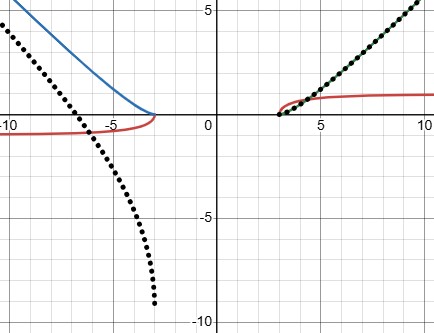
Your work, after dropping the ± signs and the absolute value, applies to the positive part, where the substitution can assume θ to be in the first quadrant:
(I modified the image to remove the ±, as well as adding conditions in red.)
What happens for negative x? One approach is to change the substitution so that θ is still in the first quadrant: x = -3 sec(θ). As you can see here, the negative sign will cancel out:
So it turns out that the naive work, ignoring signs, gives the correct answer. [But see below …]
Here I dealt with the hypotenuse in the drawing by forcing it to be positive, changing the label.
Catching my own error (again)
Signs don’t always cancel out like this! In fact, as we’ll be seeing, it really doesn’t here. My work is incorrect, and I’m leaving it here for pedagogical purposes! Can you see an error?
For fun, I graphed the definite integral on Desmos; it doesn’t let you graph an indefinite integral, because that is really a whole family of functions. The definite integral, by the FTC, accomplishes the same thing; but because the domain in non-contiguous, we can only graph it as two separate integrals:
I should point out that the definite integrals amount to indefinite integrals with the constant chosen so that the value is 0 for \(x=3\) and \(x=-3\) respectively, so it would not be wrong if we got something that differed by a constant (and, in particular, by a different constant in each branch).
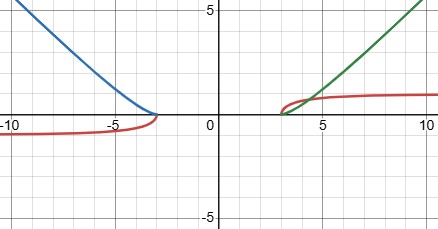
Here is the graph of your indefinite integral:
Clearly our answer is wrong in the negative case – and it’s now my answer as much as Amia’s! So I’ve made a mistake.
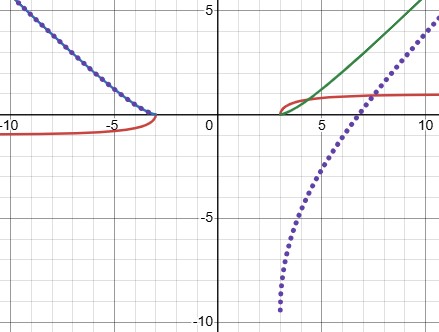
That’s a surprise, isn’t it? It agrees for positive x, but not for negative x. To fix it in the latter case, I had to change a sign and add an arbitrary constant to match my choice of limits of integration:
Clearly your answer doesn’t really work for all x, and I was wrong above when I showed the work for the negative case as giving the same answer.
So the correct answer appears to require a piecewise presentation, with a different sign (and constant) for each branch. We have to find the error in the work and obtain that answer, don’t we?
I’m going to let you find my error, which will be a good exercise, and may lead to more discussion. At the least, it will help you see the value of doing what I didn’t add to your work, namely explicitly stating the inverse substitution at the start!
Furthermore, when I give this problem to Wolfram Alpha, it gives only a single case — but it’s not quite the same as yours, and now I can see why:
This is definitely worth further discussion!
I had checked their answer before, and without looking closely I just saw that there was only one case, which led me to assume my work was right. But notice the “\(\tan^{-1}\) where we had “arcsec”. That makes all the difference, as we’ll be seeing.
An alternative approach
Amia wrote back with an entirely different solution:
I changed the method of solving.
And I need time to study your answer Dr Peterson.
This work doesn’t involve a trig substitution at all, but a rather unusual u-subs. And it’s handled in a way similar to our troublesome one in the first problem, but doesn’t have a square root to worry about, because the x in the denominator combined with the x in du to make a convenient \(x^2=u^2+9\).
It’s worth noting, also, that this substitution again is not one-to-one, and we had to solve for x in the process, so it had a chance of going wrong (as we saw last time), but it did not.
The bit of work in the middle uses long division to show that $$\frac{u^2}{u^2+9}=1-\frac{9}{u^2+9}$$ It’s possible that this approach was inspired by the Wolfram answer I’d shown.
I replied:
That looks very good.
Your first method can be “rescued” in at least two ways, and will also work well. (One way will give exactly the same answer, if I recall correctly.)
Fixing the original solution
We didn’t hear more about understanding or correcting my work; so let’s try to do that.
First, where was my error?
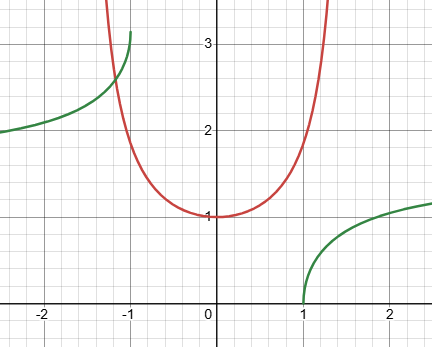
As I mentioned earlier, I neglected my usual habit of explicitly stating the inverse of the substitution, before even carrying it out. In the negative case, we defined $$x=-3\sec(\theta),$$ and specified that it is in the first quadrant. Solving for θ, we have $$\theta=\sec^{-1}(-\frac{x}{3}).$$ So the last steps of the work should have been $$\dots=3\left(\tan\theta-\theta\right)+C\\=3\left(\frac{\sqrt{x^2-9}}{3}-\sec^{-1}(-\frac{x}{3})\right)+C$$ When I looked at Amia’s work there, I believe I thought, “the secant, being the reciprocal of the cosine, is an even function, so the negative sign has no effect,” and I dropped it. (Or at least, that is what I thought as I edited that answer above!) But the inverse of an even function is not even! Here are the graphs of \(y=\sec(x)\) (red) and \(y=\sec^{-1}(x)\) (green):
The reality is that \(\sec^{-1}\left(-\frac{x}{3}\right)=\pi-\sec^{-1}\left(\frac{x}{3}\right)\), that is, the angle with a negative secant is in the second quadrant (keep in mind that here, \(-x\) is positive), and so the two angles are supplementary:
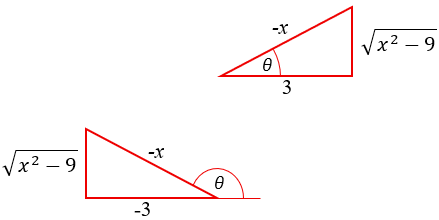
So \(\theta=\sec^{-1}(-\frac{x}{3})=\pi-\sec^{-1}\left(\frac{x}{3}\right)\), and we can continue: $$=3\left(\frac{\sqrt{x^2-9}}{3}-\left(\pi-\sec^{-1}\left(\frac{x}{3}\right)\right)\right)+C\\=\sqrt{x^2-9}-3\pi+3\sec^{-1}\left(\frac{x}{3}\right)+C,$$ just as we found.
Therefore, our answer is this piecewise function: $$\cases{\sqrt{x^2-9}-3\sec^{-1}\left(\frac{x}{3}\right)+C & if \(x\ge3\)\\\sqrt{x^2-9}-3\pi+3\sec^{-1}\left(\frac{x}{3}\right)+C & if \(x\le-3\)},$$ where the constant C might be different in the two pieces.
Avoiding pieces
Now, how can we avoid the need for cases? One way is to look back at that triangle.
The difference in the two cases was whether the hypotenuse is \(x\) or \(-x\). But who needs the hypotenuse? In both cases, \(\tan\theta=\frac{x^2-9}{3}\), and θ is in the first quadrant, so \(\theta=\tan^{-1}\left(\frac{x^2-9}{3}\right)\), and our last steps can be $$\dots=3\left(\tan\theta-\theta\right)+C\\=3\left(\frac{\sqrt{x^2-9}}{3}-\tan^{-1}\left(\frac{x^2-9}{3}\right)\right)+C\\=\sqrt{x^2-9}-3\tan^{-1}\left(\frac{x^2-9}{3}\right)+C$$
Which is what Wolfram Alpha said. Interestingly, though, this solution misses the fact that there are two disjoint parts.