Does a Linear Function Have to be Continuous?

(A new question of the week)

As we approach a new year, I want to start cleaning up a backlog of recent questions, and start posting more typical interactions, rather than waiting for the most momentous. Many of these will therefore be relatively short! This one goes back to last July, but it connects to a post from last year about the terminology of linear equations.

Here is the question, from Linda, a teacher:

Are linear functions always continuous, or can they be discrete (as in an arithmetic sequence)?

The definition given by NCTM in The Common Core Mathematics Companion defines a linear function as a relationship whose graph is a straight line, but a physicist and mathematics teacher is saying linear functions can be discrete. I always assumed they had to be continuous because lines are continuous. However, I am not well versed in high-level maths and want to be sure I give an accurate definition.

I am so grateful a group of you volunteer to continue the legacy of Dr. Math. Thank you, thank you!

Their definition clearly says that this is a linear function:

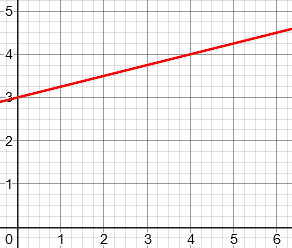
But does it mean that this isn’t, because the graph is only a set of separate points?

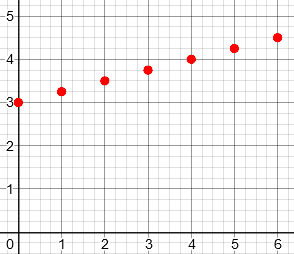
Doctor Fenton replied:

Hi Linda,

I think you are asking whether the term “linear function” can be used to describe a function whose domain is a discrete set, such as the positive integers.  Such functions are very useful, because we often want to know such things as the cost of producing n objects, given a start-up cost and cost of the materials for each object, for example.  That would be described by an equation of the form C = kn + F, where F is the fixed cost (of the machine producing the objects), k is the cost of the material needed for each object, and n is the number of objects produced.

This is a very common type of function in real life, where the input, n, is restricted to non-negative integers, while the form of the equation is such that if n were replaced with a variable x that can take real values, its graph would be a straight line. In fact, that is what my two graphs above are, with k = 0.25, and F = 3.

The NCTM description apparently assumes that the domain of the function is a continuum, a subset of the real line, but I don’t see any reason not to use the same terminology for such a function on a discrete set like the positive integers.  You could modify the NCTM description to say that the graph consists of points which lie on a straight line.  I call this a description rather than a definition, because I consider it too vague to be a definition.  It also ignores the possibility that the relationship could be of the form x = constant, which is a vertical line, but is not a function (and in particular, not a linear function).  In fact, I would call it an affine function, or linear polynomial, rather than a linear function, which would be more in line with the way “linear” is used for functions in linear algebra.

This small change, from “is a straight line” to “lie on a straight line”, that is, “is part of a straight line”, is huge!

And the observation that the only difference between the two cases is the domain, is an important clarification. To a mathematician, the domain is an essential part of the function (my two graphs above are graphs of different functions), but the relationship can be otherwise the same, and that is what makes it linear, not the domain. It’s possible that the NCTM authors were thinking only of the relationship, and not of the domain.

I’ll have comments on the last sentence, about affine functions, below.

Linda responded,

Thank you so much for clarifying the concept of linear functions, Dr. Fenton. I’ll use what you have suggested, “a relationship whose graph consists of points which lie on a straight non-vertical line,” which is likely a sufficient description for grade 8 students.

I joined the conversation with two supplemental thoughts. First:

Hi, Linda.

I’d like to add just a couple additional ideas.

I fully agree with Doctor Fenton’s thoughts, particularly his statement, “I don’t see any reason not to use the same terminology for such a function on a discrete set like the positive integers.”

It is very common for educators to state definitions that are a little too restrictive, or a little too loose, based on their own contexts. The concept of a linear function starts with the idea of a straight line (hence the term “linear”); and we generally introduce it in the context of functions of a real variable, where the graph is literally a straight line. The functions you are referring to are simply restrictions of linear functions to a discrete domain, and the name still makes sense in that context, as in fact the graph is still part of a straight line.

Generalizations from a basic starting point are common in mathematical definitions; educators may stick with the starting point, focusing on where the student is, and so may not look ahead to where the student may be later.

Second:

You may be wondering about Doctor Fenton’s mention of an alternative definition by which what you know as linear functions are properly called “affine functions”. For a brief summary of that distinction, see Wikipedia on Linear function. This distinguishes the two contexts he referred to; everything before college (and much in college for non-math majors) lies in the first context, where “linear” means what we are discussing.

In a further Wikipedia page on Linear function (calculus), there is a reference to “Arithmetic progression, a linear function of integer argument“, which exactly fits your question. The relationship is linear; the domain is discrete.

Last year I discussed the term “linear equation” with an emphasis on how the term has been broadened from its initial literal mean of “line”; what you are asking about is a considerably smaller modification than the issue there!

The first Wikipedia article identifies the two contexts as

1. “In calculus, analytic geometry and related areas, a linear function is a polynomial of degree one or less, including the zero polynomial (the latter not being considered to have degree zero).” – we could describe this as “calculus and below”, which includes high-school level algebra. This is where the equation of any line is considered linear.
2. “In linear algebra, a linear function is a map f between two vector spaces that preserves vector addition and scalar multiplication: \( f(\mathbf {x} +\mathbf {y} )=f(\mathbf {x} )+f(\mathbf {y} )\); \(f(a\mathbf {x} )=af(\mathbf {x} )\)” – more broadly, this is related to abstract algebra, which goes far beyond high-school algebra, taking it to any sort of structure that is comparable to numbers and their operations. Here, “linear” is restricted, in effect, to lines through the origin – though in this context, we are far beyond such simple graphs.

This can be confusing! For a little on the relationship between high-school algebra and abstract algebra, see

The Algebra that High School and College Share in Common

Linda responded:

Hi, Dr. Peterson,

Thanks so much for your helpful reply and links. You make a good point about definitions that are too loose or too restrictive, based on our own contexts as teachers (I fell right into that trap myself). I also appreciated reading about the two distinct concepts for the phrase linear function, which I had not considered. A linear function with a discrete domain is exactly what an arithmetic sequence is, and its points certainly lie on a line. I think the most helpful part of your answer was the discussion on linear equation. It gave me a good deal to think about. The discussion and points you bring up with Christine will help me better understand confusion about the use of the word “linear” with regard to all students, but particularly ESL students.

Thanks again for your time, and for such a thorough and understandable reply.

Linda

One of the tricks in teaching, when you know more advanced math, is to recognize the context of a question, and use language appropriate to it! And Linda’s laudable desire to use accurate definitions that will be suitable for her level, but will not become inconsistent with later learning, for those who go further, is complicated by the fact that language sometimes changes as you advance. But I think we have done as well as we can.