There are so many ways to find a Least Common Multiple that I had to omit one method we have been asked about several times. This one doesn’t require finding prime factors, but focuses on division by whatever factors you see.
Divide everything by whatever works
The first reference to the method I have found in our archive was in 1997:
Least Common Multiple The question I have is about how to find the least common multiples from a set of numbers. I know that a multiple of a number has that number as one of its factors. What is the least common multiple for the numbers 5 and 25? Is there a stated rule or definition for least common multiples? Thanks!
This is actually a spectacularly easy example, as 25 is itself a multiple of 5, so that is the LCM. But the question is mostly a request for a general method. Doctor Sebastien answered with a method different from the others we’ve seen:
The least common multiple (L.C.M.) of a set of numbers is the smallest number that is a multiple of all numbers in the set.
The way I was told to find the LCM of a set of numbers was
1. Align them in a line.
2. Then divide all numbers by an appropriate integer.
3. If any number is not divisible by that integer,
don't divide that number and leave it untouched.
4. Repeat steps 2 and 3 until all 1's are obtained.
5. Then multiply all the divisors together.
The answer is the LCM.
To better explain what I mean, I will find the LCM of 5 and 25.
STEP 1: 5, 25
1, 5
-------
STEP 2: 5 | 5, 25
1, 1
--------
STEP 3: 5 | 1, 5
In the previous step, the 1 is left untouched because it is not divisible by 5. The LCM is then 5*5 = 25.
Here we saw that we could divide both numbers by 5, so we did that, and were left with 1 and 5. Now we divide only the one number that can still be divided; the LCM is the product of all the divisors we used.
Let’s go a little beyond the example he gave …
One way to organize this is to pile one division on top of another:
1 1 --------- 5 ) 1 5 <-- divide only 5 by 5 --------- 5 ) 5 25 <-- divide both by 5 ^ | +--- LCM = 5*5 = 25
Let’s try it for a hard case; I’ll use 100 and 120:
1 1 ------------ 6 ) 1 6 <-- divide only 6 by 6 ------------ 5 ) 5 6 <-- divide only 5 by 5 ------------ 2 ) 10 12 <-- divide both by 2 ------------ 10 ) 100 120 <-- divide both by 10 ^ | +--- LCM = 10*2*5*6 = 600
Notice that we don’t have to divide by primes; I saw 10 as an obvious divisor, so I used it. Also notice that at the end, I didn’t really have to divide by the 5 and the 6, as long as I saw that there were no common divisors left. I could have just used them as the last factors:
5 6 <-- no common factors left ------------ 2 ) 10 12 <-- divide both by 2 ------------ 10 ) 100 120 <-- divide both by 10 ^ | +--- LCM = 10*2*5*6 = 600
This is a more refined version of the method, which we’ll be seeing below with even more added features.
A layer cake
A 2012 question specifically asked about this method:
Layers of Least Common Multiples I recently learned how to find the least common multiple (LCM) of two or more numbers using "the upside-down birthday cake method." For example, if you were looking for the LCM of the numbers 14 and 18, you would draw an "L" or upside down division "house" with a long base, and put the 14 and 18 on the base. Then you put a common factor outside the "L," and underneath each of the numbers, you write the other factor. (This is much easier to show than explain; my apologies.) When you arrive at a layer where there are no more common factors (besides one), you multiply the numbers outside the "L" on the left with the numbers in the bottom-most layer. Why does this work? I'm trying to understand the why/how aspect. I know it's breaking the numbers down into common factors...?
Here we are flipping my stack of divisions upside-down, but it’s the same idea. Doctor Ian answered, first showing his understanding of the method (which was in fact well explained):
Hi Zoe,
I think you mean something like this; using a slightly more interesting pair of numbers,
12 18
_________________
2' | 6 9 <- 12 = 2*6, 18 = 2*9
3' | 2' 3' <- 6 = 3*2, 9 = 3*3
^
|________________________ Multiply the terms marked with a '
to get the LCM.
Is that right?
What Zoe described as “the other factor” on the inside can be just as well called “the quotient”, the result of dividing by the factor on the left. The LCM is \(2\times3\times2\times3 = 36\), which is indeed the LCM.
Why it works
So, why does this work? He compares it to what I called Method 2b last time, listing prime factors of each number and pairing them up:
If so, maybe it's easiest to see what's going on if you think about the more normal way of doing this, which is to break both numbers into prime factors:
12 = 2 * 2 * 3
18 = 2 * 3 * 3
The least common multiple will be the one that shares all the prime factors. In this case, it's 36:
These are not shared; they are
the ones that end up at the
_____________ bottom in the "cake" method.
| |
v v
12 = 2 * 2 * 3
18 = 2 * 3 * 3
LCM = 2 * 2 * 3 * 3
^ ^
|_______|_________ These are shared; they are
the ones that end up to the
left in the "cake" method.
(Do you see why collecting factors like this gives us the smallest number that can be divided by both 12 and 18? If we remove any of those prime factors, we'd be missing at least one prime factor from one of the numbers. If we add any more prime factors, we'll have a number that is larger than we need.)
Whether you divided separately by the common prime factors 2 and 3, or all at once by the common factor 6, you will still get the same result in the end.
What you were doing was a little harder, since you have to keep identifying common factors -- but it amounts to the same thing:
12 = 2 * (2 * 3)
18 = 2 * (3 * 3) Identify the first common factor
12 = 2 * 3 * (2)
18 = 2 * 3 * (3) Identify another one
12 = (2 * 3) * (2)
18 = (2 * 3) * (3) No more common factors.
The product we've pulled out
contains the shared prime
factors, and the remaining
ones are not shared.
The benefit of the method is that you don’t have to find prime factors first; you can just take it as you see it.
Why it’s not the best way
The downside is that you have to see common factors, which is not always easy without using primes:
However, pick two numbers with less obvious prime factors -- for example,
1938 3534
___________________
2 | 969 1767
3 | 323 589
It might be tempting to quit at this point, thinking that this is the LCM:
2 * 3 * 323 * 589 = 1,141,482
Now compare that to using the prime factor method:
1938 = 2 * 3 * 17 * 19
3534 = 2 * 3 * 19 * 31
LCM = 2 * 3 * 17 * 19 * 31
This way, it's easy to see that the LCM is actually
2 * 3 * 17 * 19 * 31 = 60,078
This is still large, but significantly smaller.
What happened here is that there were (intentionally) some larger prime factors that you might not think to try.
So the nice thing about the prime factor method is that there's no way to quit too early. Also, it directly relates the idea of prime factors to the idea of "least common multiple," and doesn't require you to memorize a made-up method for calculating that without really understanding what you're doing. :^D
On the other hand, you are in fact focusing on common factors, and pulling those out is just what you need to make a common multiple as small as possible.
By the way, have you noticed that the left-hand-column of the work is the GCF? The method amounts to saying, $$\text{LCM}(A,B)=\frac{AB}{\text{GCF}(A,B)}=\text{GCF}(A,B)\cdot\frac{A}{\text{GCF}(A,B)}\cdot\frac{B}{\text{GCF}(A,B)}$$
Zoe wasn’t quite satisfied:
Thank you very much! I guess I understand slightly better... My only immediate thought is that in making prime factor trees (if that was the method to find the prime factors of each), couldn't one make the same mistake in prematurely believing one has enumerated all the prime factors? In short, the "danger" of stopping short still seems possible. It's so frustrating to not have the deeper understanding :(
Exactly a point I was going to make! When there are larger primes to discover, you can just as well miss them while looking for prime factors. (This is where the Euclidean algorithm comes to the rescue, for very large numbers.)
Seeing the bones
Doctor Ian had more to say:
Stopping short could happen, but if you're used to finding prime factorizations -- which is something that you do in lots of different contexts -- then it seems less likely. And you can use things like tables of primes to check whether you're down to primes or not. For finding common factors of two numbers, on the other hand, there's nothing comparable. So I think the two "dangers" are slightly different in nature.
If I were looking for those remaining common factors, I would probably be going through a list of primes and trying one after another, whichever method I was using. That work is not shown in either method, usually.
But how about that matter of “understanding”?
I agree it's frustrating to lack deeper understanding, and we shouldn't stop until we have it. On that note, I'm not sure what you're not understanding at this point! Do you understand why, when we have prime factorizations for two numbers, e.g., ...
12 = 2 * 2 * 3
18 = 2 * 3 * 3
... we can collect those in different ways to find the greatest common factor (GCF) and the LCM?
12 = 2 * 2 * 3
18 = 2 * 3 * 3
GCF = 2 * 3
LCM = 2 * 2 * 3 * 3
In some sense, the "deepest" you can go here in terms of explanation is the Fundamental Theorem of Arithmetic, which says that every integer greater than 1 has exactly one prime factorization, and every prime factorization corresponds to exactly one number. Are you familiar with that?
The FTA tells us that we can always find a prime factorization, and there is only one correct answer (as long as you ignore order, or always write the primes in increasing order).
Think of prime factors as a kind of x-ray: they let you see the internal structures of numbers. For example, I could have a bunch of numbers:
51
391
731
816
These might not seem to have anything in common -- but when I look at their "x-rays," I can see that they all share one multiple in common:
51 = 3 * 17
391 = 17 * 23
731 = 17 * 43
816 = 2 * 2 * 2 * 2 * 3 * 17
Primes are the “bones” of numbers, and seeing them is very helpful!
Is there anything about this that still seems mysterious to you?
Now Zoe got it:
Yes! That did it! Thank you!! I was not familiar with the Fundamental Theorem of Arithmetic, but it clicked as soon as you compared it to an x-ray and looking at what the number is made up of!
So we’ve seen both how the method works, and why it is not the best. But it’s still yet another tool in our toolbox, to be used when the numbers are fairly small; if we are unsure whether we’ve found all the common factors, it’s time to pull out the x-ray machine!
Digging deeper
In 2006, a student had submitted what amounts to the same method:
One Approach to Finding LCM and GCF at the Same Time I just wanted to show you something I learned recently on how to find the LCM and GCF at the same time. You make a chart with the two numbers in question, let's say 12 and 8: 12 ** 8 Now you decide what number can go into both, like 2 or 4. Let's choose 4, and write it on the left: 12 ** 8 4* Now ask how many times does 4 go into 12 and put it under the 12, then same with 8: 12 ** 8 4* 3 ** 2 Now make sure you can't put any number other than 1 into 3 and 2 (if we chose 2 in the first place we would have to do the process again). Anyway we're done with this one, now the 4 in the left is the GCF and then we multiply the GCF with the bottom row (in this case the 3 and 2) ... 4 x 3 x 2 = 24 which is our LCM. This also works with 3 numbers but they have to all have a GCF other than 1 otherwise it's more work and not really worth the hassle. Hope this can help others!
I replied, comparing it to the way we simplify fractions in small steps rather than having to find the GCF and simplify all at once:
Hi, Lindsay. Thanks for sharing your method. I like it! It corresponds to what I recommend in simplifying fractions, that you take it in steps, just dividing by whatever you see that is a common factor, and then repeat until there's nothing left. In fact, that's exactly what you're doing here, with the bonus of getting the LCM at the end.
When I say that is what she is doing, I mean this: Her work is just what you’d do in simplifying \(\frac{12}{8}\) by dividing both numbers either by 4 all at once, or by 2 and then by 2 again. The GCF is the product of all the numbers you’ve divided by. The new thing is that the LCM is the product of that and the numbers in the simplified fraction!
Let me try it in a more complicated case.
Suppose we want to find the GCF and/or LCM of 54 and 90. I first see that they are both even, so I divide by 2:
| 54 | 90
--+----+----
2 | 27 | 45
Now I see that 27 and 45 are both multiples of 9, so I divide by that:
| 54 | 90
--+----+----
2 | 27 | 45
9 | 3 | 5
Now I can't divide any more. The GCF is the product of the numbers down the side, 2*9 = 18, and the LCM is the product of the whole L on the left and bottom, 2*9*3*5 = 18*15 = 270. At the same time, the ratio 54:90 or the fraction 54/90, simplified, is sitting there as well, 3:5 or 3/5.
This example is more typical, and shows the value of the method (when the final numbers are small enough to be sure they are relatively prime).
Also, it seems very natural that the product of the factors should be the GCF, so it's easy to remember how to get that. The LCM is more magical, but I can see how to explain why it works: in order to get a multiple of 54, we have to multiply the GCF by the 3, and in order to get a multiple of 90 we have to multiply by the 5, so using both gives us a common multiple.
We can relate this to the Venn diagram method from last time:
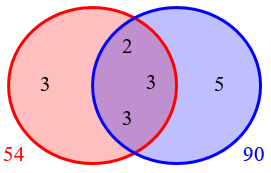
The intersection (GCF) is the left column, and the left and right parts are the bottom row. Their product is the LCM.
How about three numbers? I don't think the LCM part would work at all. I'll try this one:
| 54 | 90 | 70
--+----+----+----
2 | 27 | 45 | 35
No, the LCM isn't going to work, since we only need one extra 5, for example, not both 45 and 35 in the mix--do you have a way to do it? I think I can come up with something, but not just now.
More than two numbers?
In 2010, Michelle took me up on the idea of extending the method to three numbers, in addition to asking for more explanation:
LCM and GCF, Combined: Why and How On 03/02/2006, Doctor Peterson answered a question about a method for finding the least common multiple (LCM) and greatest common factor (GCF) at the same time. Basically, you keep taking common factors out until there is nothing else in common. The product of the GCF column ends up being the GCF, and the GCF multiplied by uncommon factors is the LCM. I understand how to use this method but I am still confused as to why the method works for LCM -- it seems like magic instead of math -- and why it does not work when comparing three numbers. I have been trying to come up with my own method for triples, but I have been unsuccessful. Please help soon. I mainly need a good way to explain why the method works. Here's an example with two numbers: GCF / 12 / 20 4 / 3 / 5 According to the method, GCF = 4 LCM = 4 * 3 * 5 = 60 Here's an example with three numbers: GCF / 10 / 4 / 20 2 / 5 / 2 / 10 So, GCF = 2 LCM = 2 * 5 * 2 * 10 = 200 But the LCM for those three numbers is actually 40. How do I fix this? And why does it work for two numbers in the first place?
Another explanation
I answered, “showing the bones” as Doctor Ian did:
Hi, Michelle.
I DID explain how the LCM works there; but there are other ways to say it.
Let's write the numbers as products of (powers of) primes to see more clearly what is happening. I'll do it in two steps rather than one, to make it somewhat more typical:
| 4*3 | 4*5
--+-----+-----
2 | 2*3 | 2*5
2 | 3 | 5
The GCF is the product of the numbers on the left (the divisors), because 12 is 2*2*3 (the GCF times what's left over), and likewise 20 is 2*2*5.
Now, how do we find the LCM? We can start with the GCF and multiply by whatever else we need to get each number. In each case, we need to multiply by that left-over number at the bottom of the column. Starting with 4, we have to multiply by 3 to get a multiple of 12; and by 5 to get a multiple of 20. So the smallest possible multiple of both is made by multiplying the GCF by BOTH 3 and 5: 2*2*3*5.
Applying a method to a more visible case (doing it under x-ray, we might say) can be a good way to observe how it works!
In general, two numbers a and b can each be written as multiples of their GCF (say d), so that a = dx and b = dy. Then the product of the factors on the left will be d, and the numbers on the bottom will be x and y. The LCM is dxy, since this is a multiple of both dx and dy, and no smaller multiple will work.
| dx | dy
--+----+----
d | x | y GCF = d, LCM = dxy
Extending it to three
By this time I had taught a Math for Elementary Teachers course, whose textbook included this method, so I had an answer (which, it turns out, was hidden in the 1996 method we started with, which I had probably never seen):
I've since learned a way to do this for more than two numbers. All we do is continue dividing after we have run out of common divisors, using factors of some, rather than all, of the numbers.
Here is the work for the example I tried on that 2006 conversation that you referenced:
| 54 | 90 | 70
--+----+----+----
2 | 27 | 45 | 35 <-- 2 divides ALL the numbers
--+----+----+----
9 | 3 | 5 | 35 <-- 9 divides TWO of the numbers
5 | 3 | 1 | 7 <-- 5 divides TWO of the numbers
Once we are down to only distinct primes in the bottom of the columns -- or, at least, the numbers are pairwise relatively prime -- we have both the GCF (2), from the top part of the left column; and the LCM (2*9*5*3*1*7 = 1890), from the entire left and bottom.
It’s important to continue until no two numbers at the bottom have any common factors.
For comparison, the usual method gives 54 = 2^1*3^3 90 = 2^1*3^2*5^1 70 = 2^1 *5^1*7^1 -------------------- GCF = 2^1 = 2 LCM = 2^1*3^3*5^1*7^1 = 1890
I do think that method is clearer and surer; but this method still has interest.
