We’ve looked at positive integer powers of complex numbers, and imaginary powers of e. Now let’s look at roots of complex numbers, which will bring us to the idea that led to this series, namely the roots of unity.
Square root of i, by algebra
We’ll start with three different perspectives on the same problem, \(\sqrt{i}\). First, from 2003:
The Square Root of i What is the square root of i?
This question was actually asked in 1997, but an answer to an identical question from Doctor Schwa was appended to the page, which makes a good intro:
Good question! When I was in high school and confronted with this same problem, it seemed obvious to me that the answer must be "j". Just like we needed to invent a new number "i" to be the square root of -1, it seemed like we'd need yet another new kind of number to be the square root of "i", and so on forever.
Since we had to “invent” a square root of \(i\), shouldn’t we have to keep doing that? Amazingly, no!
The amazing thing is that you don't: once you have "i", any equations with addition, multiplication, exponents and so on (in short, any polynomial), can be solved without inventing any new types of numbers! An equation like x+3 = 2 makes you invent negatives, x*3 = 2 makes you invent fractions, x*x = 2 makes you invent irrationals, x*x = -2 makes you invent imaginaries... but then you're done!
This is what make complex numbers central to much of modern mathematics. They are the ultimate kind of number (in this sense … there are actually more, but they’re very different).
On to the question itself: Just as the square root of 4 is a number whose square is 4, here we want a (complex) number whose square is i.
So, once I knew it was possible, and that the answer had to be some complex number (a+bi), the question is, how do you find out values of a and b that will make (a+bi)^2 = i? Well, squaring out the left side gives a^2 + 2ab i - b^2 = i, and the only way for that to work is if the real number part is 0, a^2 - b^2 = 0, and the imaginary part is 1*i, 2ab = 1.
So because we are assuming a and b are real numbers, our single equation \((a+bi)^2=i\), which is equivalent to \((a^2-b^2)+(2ab)i=i\), becomes a system of two (non-linear) equations: $$a^2-b^2=0\\2ab=1$$ This is not hard to solve. (We’ll see harder examples later.)
Since a^2 = b^2, a = b or -b ... but since 2ab = 1, a and b must be both positive or both negative, so a = b. Then since 2ab = 1, and a = b, 2aa = 1, so a^2 = 1/2, and a = b = sqrt(1/2) or a = b = -sqrt(1/2)! Does that make sense?
That gives us the answer: $$a+bi=\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}i\text{ or }-\frac{\sqrt{2}}{2}-\frac{\sqrt{2}}{2}i.$$
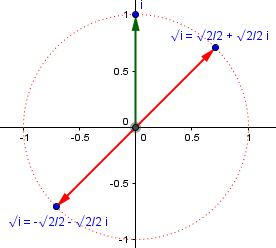
As usual, there are two square roots. More on that later!
For another presentation of this approach, starting with the definition of complex numbers as ordered pairs, see
Square Root of i
For a different approach to the algebra, see
An Algebraic Derivation of the Square Root of i
Square root of i, by DeMoivre
But algebra isn’t the only way, or the most powerful. Here is Doctor Anthony’s brief answer to the 1997 question:
We have i = cos(pi/2) + i.sin(pi/2)
sqrt(i) = (cos(pi/2) + i.sin(pi/2))^(1/2)
By DeMoivre's theorem:
= cos(pi/4) + i.sin(pi/4)
1 + i
= ----------
sqrt(2)
Since the argument (angle) of i is \(\frac{\pi}{2}\), or 90°, and the square root is the \(\frac{1}{2}\) power, he just plugged these into DeMoivre’s formula, $$(\cos(x)+i\sin(x))^n= \cos(nx)+i\sin(nx),$$ to get $$\left(\cos\left(\frac{\pi}{2}\right)+i\sin\left(\frac{\pi}{2}\right)\right)^\frac{1}{2}= \cos\left(\frac{\pi}{4}\right)+i\sin\left(\frac{\pi}{4}\right)=\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}i,$$ which is the same result as before:
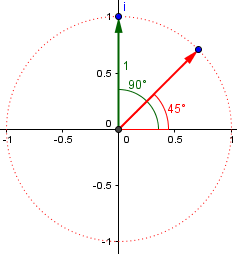
So taking the square root of a number takes the square root of the modulus (length), and halves the argument (angle).
But .. what about the other root? For some reason he omitted that. (We’ll see him get this right in a later answer!)
This is where roots get tricky using this method. Recall from trigonometry that any angle has “coterminal angles” that start and end in the same place, but go around different numbers of times. Our 90° angle could also be called 450° (by adding 360°), or -270° (by subtracting 360°), and so on. When we divide those by 2, we get 225° or -135°, respectively. Either of those gives the same second root:
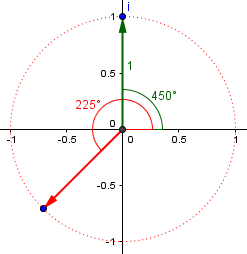
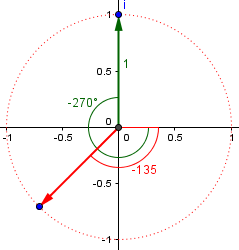
In general, since we can add any multiple of \(2\pi\) to an angle, when we divide it by 2, we are adding any multiple of \(\pi\) to our square root, which gives us roots that are 180° apart, as here:
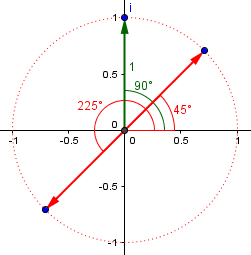
Note that if we square either of these, we get i, by doubling the angle.
Square root of i, by Euler
Here is yet another version of the same question, from 1999:
Square Root of i In my Honors Algebra II/Trigonometry class, we just completed a section on complex numbers. One of my students asked me the following: The square root of -1 is i, but what is the square root of i? Can you help?
Doctor Rick answered, starting with a warning:
There are two complex numbers which, when squared, equal i. (The same holds true for any number. But for real numbers, we arbitrarily say that the positive root is THE square root. When the roots have imaginary parts, any such choice would be even more arbitrary, and we do not bother to choose one.)
This is an interesting point: Not only are there two roots, but we can’t call one of them the principal root, in the same way we do in saying that \(\sqrt{9}=3\text{, not}-3\). One reason is that neither root is positive, which applies only to real numbers, so we can’t use the rule we are used to; another is that whatever rule we used, it would not always be true that \(\sqrt{w}\cdot\sqrt{z}=\sqrt{wz}\) for all complex numbers w and z. We could arbitrarily choose to call one of them the principal root (and do, for some purposes), but that doesn’t make everything work as expected, as it does for real numbers! This will be the topic of another post someday.
In particular, when textbooks say to write \(\sqrt{-1}=i\), it is just for convenience, and doesn’t mean that is really the root.
The square roots of i are (1 + i) * sqrt(2)/2 and -(1 + i) * sqrt(2)/2 You can prove this just by squaring each number. To find them in the first place, you can use Euler's formula e^(i*t) = Cos(t)+i*Sin(t) If t = pi/2, you get e^(i*pi/2) = cos(pi/2)+i*sin(pi/2) = 0 + i*1 = i The square root of this is (e^(i*pi/2))^(1/2) = e^(i*pi/4) and using Euler's formula again, we have e^(i*pi/4) = 1/2 + i*1/2
But we aren’t finished, are we?
If you set t = 5*pi/2, you again get e^(i*5pi/2) = i. Taking the square root of this and using Euler's formula, you get the other root of i.
This can be easy to forget, whatever method you use. You need to keep in mind that there will be two square roots (and three cube roots, four fourth roots, and so on). Or, just use the general form: $$\left(e^{i\left(\frac{\pi}{2}+2k\pi\right)}\right)^\frac{1}{2}=e^{i\left(\frac{\pi}{4}+k\pi\right)}.$$
The angles \(\frac{\pi}{2}\) and \(\frac{5\pi}{2}\) are the 90° and 450° we saw before.
Euler's formula makes it easy to find powers and roots by working in polar coordinates in the complex plane. Any number x + iy can be written in terms of a radius r and angle theta (counterclockwise from the x axis):
x + iy = re^(i*theta)
r = sqrt(x^2 + y^2)
theta = arctan(y/x)
Then, using Euler's formula,
(x+iy)^k = r^k e^(i*k*theta)
= r^k(cos(k*theta) + i*sin(k*theta))
This amounts to the proof of DeMoivre we saw last time. But don’t forget to adjust \(\theta\) to be in the right quadrant.
Square root of 3+4i, by algebra
How about the square root of a complex number other than i? Here is a (poorly titled!) question from 2002:
Finding the Square Root of a Quadratic Function I was recently assigned the problem Find the square root of 3+4i I am in advanced college math and am totally stumped by this question. Please help me...
Doctor Paul answered, using the algebraic approach:
If sqrt(3+4*i) = a + b*i where a and b are real numbers, then squaring both sides gives:
(a + b*i) * (a + b*i) = 3 + 4*i
a^2 + 2*a*b*i - b^2 = 3 + 4*i
equating coefficients gives:
a^2 - b^2 = 3
and
2*a*b = 4
These are the same equations we saw before, but with different constants on the right, which make us do a little more work this time:
Solve for b in the second equation and substitute into the first equation:
b = 2/a
so
a^2 - (2/a)^2 = 3
a^2 - 4/a^2 = 3
multiply both sides by a^2:
a^4 - 3*a^2 - 4 = 0
The substitution left us with a variable on the bottom, so we cleared that and got what is sometimes called a biquadratic equation.
This is quadratic in a^2 so we make a substitution:
Now let x = a^2
So we have:
x^2 - 3*x - 4 = 0
(x-4)*(x+1) = 0
So x = 4 or x = -1
This gives
a = 2, -2, i, -i
We said above that a had to be real, so it must be the case that a = 2 or a = -2.
Now, if a = 2 then b = 1
and if a = -2 then b = -1
So we have:
sqrt(3 + 4*i) = (2 + i) or -(2 + i)
Each of the two solutions for x gives us two solutions for a, and each real value of a yields a corresponding value for b. Here are our roots:
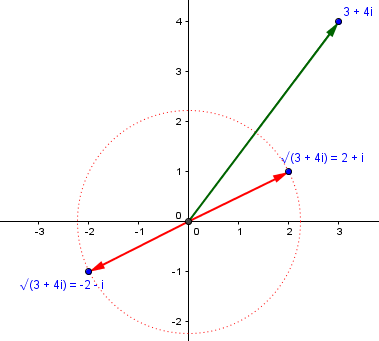
We could also do this using Euler or DeMoivre.
Complex cube roots, by DeMoivre
Enough of square roots; let’s take it up a notch, with this question from 1997 on cube roots:
Cube Roots of Numbers If x^3 = N, where N is some expression (which could be a constant), then you have a degree three equation so there must be three roots. If you take i (sqrt(-1)), then the cube root is -i. But since x^3 = i is degree three, there should be three different values of x. What are they? How do you determine these three values for other numbers? Is there a formula? Please help.
Presumably Jared found the one answer just by recognizing that \((-i)^3=(-i)(-i)(-i)=(-i)(-1)=i\). He recognizes that the cubic equation should have three solutions (though sometimes there can be fewer due to multiplicity). We’ve seen pairs of square roots; how can we find triples of cube roots?
Cube roots of 8
Doctor Anthony answered, focusing first on the general idea of getting three roots, rather than the specific example of \(\sqrt[3]{i}\):
You are quite right that there will be 3 cube roots of a number. You do need to work with complex numbers, however, to understand how to find the three roots, so if what I show you is not clear, it will become so when you have studied complex numbers.
Suppose z^3 = 8
Now taking the cube root of each side you would say that z = 2, however, there are two other cube roots which we shall now find.
Since cos(2k.pi) = 1 and sin(2k.pi) = 0 where k is any integer, we could write the equation
z^3 = 8(cos(2k.pi) + i.sin(2k.pi))
The key here is to take into account all representations of the angle, not just the principal argument. The real number 8 has angle 0, but also any multiple of 360° more or less than that – that is, any integer multiple of \(2\pi\). So we write 8 not just as $$8\left(\cos(0) + i\sin(0)\right)$$ but as $$8\left(\cos(2k\pi) + i\sin(2k\pi)\right).$$
Take cube root of both sides, and use deMoivre's theorem which shows that:
[cos(x) + i.sin(x)]^(1/3) = cos(x/3) + i.sin(x/3) to get
z = 2[cos(2k.pi/3) + i.sin(2k.pi/3)] k = 0, 1, 2
k=0 gives z1 = 2(cos(0) + i.sin(0)] = 2 (the one real root)
k=1 gives z2 = 2(cos(2.pi/3) + i.sin(2.pi/3)) = 2(-1/2 + i.sqrt(3)/2)
k=2 gives z3 = 2(cos(4.pi/3) + i.sin(4.pi/3)) = 2(-1/2 - i.sqrt(3)/2)
If we give k more values, 3, 4, 5, ..... we simply repeat the three roots already found.
If we didn’t know to expect three roots, we would just keep going until we found that we were repeating. So, rather than explicitly memorizing how many roots there are, we just have to keep the periodicity of the trig functions in mind.
If you represent the three roots on an Argand diagram that has real values along the x axis and imaginary values on the y axis, the three roots will appear as the three spokes of a wheel, with the z values lying on a circle of radius 2 units. One root will lie along the positive x axis, and the other two at +120 degrees and -120 degrees to the x axis. So the roots are symmetrically spaced round the circle. In fact this is always the way that cube roots of a real number will look. If you take the cube root of an imaginary number, say i, then you still get three spokes but they will be rotated round to lie along the 30 degree, 150 degree and 270 degree lines on the unit circle.
Here are the three cube roots of 8: $$z_1=2\left(\cos(0)+i\sin(0)\right)=2\\z_2=2\left(\cos\left(\frac{2\pi}{3}\right)+i\sin\left(\frac{2\pi}{3}\right)\right)=-1+i\sqrt{3}\\z_3=2\left(\cos\left(\frac{4\pi}{3}\right)+i\sin\left(\frac{4\pi}{3}\right)\right)=-1-i\sqrt{3}$$
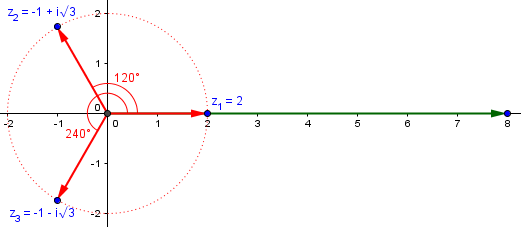
We could instead have solved this algebraically: $$z^3-8=0\\(z-2)(z^2+2z+4)=0\\z_1=2,z=\frac{-2\pm\sqrt{-12}}{2}\\z_2=-1+i\sqrt{3},z_3=-1-i\sqrt{3}$$
Cube roots of i
How about the cube roots of i? Here they are, by the same sort of work:
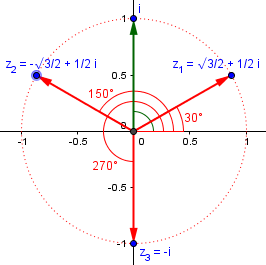
In this case, the angle for i is $$\frac{\pi}{2}+2k\pi=\frac{4k+1}{2}\pi=\frac{\pi}{2},\frac{5\pi}{2},\frac{9\pi}{2},\dots.$$ so the angle for its cube root is 1/3 of that, namely $$\frac{4k+1}{6}\pi=\frac{\pi}{6},\frac{5\pi}{6},\frac{9\pi}{6}=\frac{3\pi}{2}.$$
So $$z_1=\cos\left(\frac{\pi}{6}\right)+i\sin\left(\frac{\pi}{6}\right)=\frac{\sqrt{3}}{2}+\frac{1}{2}i\\z_2=\cos\left(\frac{5\pi}{6}\right)+i\sin\left(\frac{5\pi}{6}\right)=-\frac{\sqrt{3}}{2}+\frac{1}{2}i\\z_3=\cos\left(\frac{3\pi}{2}\right)+i\sin\left(\frac{3\pi}{2}\right)=-i\\$$
Now, can we solve this one algebraically? As Jared said, we need to solve the equation $$z^3-i=0$$ Knowing that one root is \(-i\), we can factor using the familiar formula for a difference of cubes, $$a^3-b^3=(a-b)(a^2+ab+b^2)$$ and obtain $$z^3-(-i)^3=(z+i)(z^2-iz-1)$$ So all we have to do is to solve $$z^2-iz-1=0$$ using the quadratic formula: $$z=\frac{i\pm\sqrt{(-i)^2-4(1)(-1)}}{2}=\frac{i\pm\sqrt{3}}{2}=\pm\frac{\sqrt{3}}{2}+\frac{1}{2}i$$
I don’t believe I’ve ever done that before!
Fifth roots of 2+3i, by Euler
Now let’s put it all together (a higher root of a complex number), with this question from 2005:
Finding Roots of Complex Numbers How do you find the nth roots of a complex number a + bi?
Doctor Jerry answered with a specific example:
Hello Kira,
I'll answer by showing how to find the fifth roots of 2 + 3i.
We convert 2 + 3i to polar form and look for complex numbers in the polar form
r*e^{i*t} = r*(cos(t) + i*sin(t)).
Since 2 + 3i = sqrt(13)*e^{i*arctan(3/2)}, we want
( r*e^{i*t} )^5 = sqrt(13)*e^{i*arctan(3/2)}
This is
r^5*e^{i*5t} = sqrt(13)*e^{i*arctan(3/2)}
This time the numbers don’t work out quite as nicely as for our previous examples, so this is more typical. But notice that he doesn’t just take the 1/5 power. Instead, he solves an equation, by setting moduli and arguments equal, much as we have elsewhere set real and imaginary parts equal. (The same thing would work if you used DeMoivre but were only allowed to use integers, because the general case had not been proved yet.)
We see that r^5 = sqrt(13) and so r = [13^(1/2)]^(1/5)] or 13^(1/10) and also that 5t - arctan(3/2) = 2*pi*n, n = 0,1,2,3,4 So, t = [2*pi*n + arctan(3/2)]/5, n = 0,1,2,3,4.
He finds the general solution to the trigonometric equation, and takes the first 5 solutions.
Let's look at one of these "fifth roots." Take n = 3.
r = 13^{1/10} = 1.29239222078083
t = [2*pi*3 + arctan(3/2)]/5 = 3.96646992895723
r*e^{i*t} = -0.87707824256 - i*0.949216207595
The fifth power of this complex number is 2 + 3*i.
Here are our roots, with the \(n=0\) and \(n=3\) cases marked out:
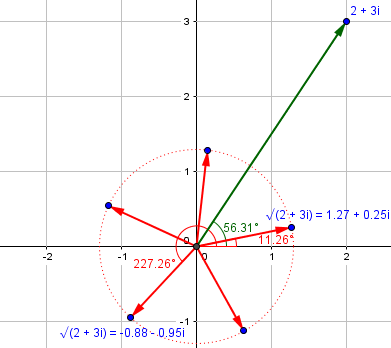
Roots of unity
Now look at that last picture. There are two parts to finding these roots. We can find the first root by just dividing the argument of the radicand by 5:
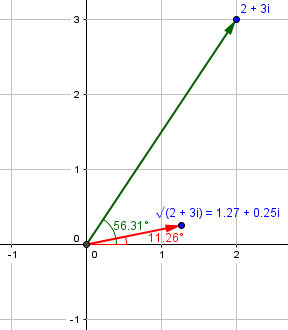
Then we can find the others by multiplying this by the five “fifth roots of unity” (“unity” being a name for “1”), which are 1 and four others:
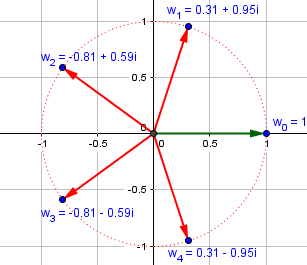
We can talk similarly about the nth roots of unity for any positive integer n; they form an n-gon inscribed in the unit circle.
