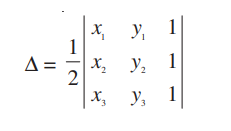(A new question of the week)
A recent question asked for the connection between two different ways to use determinants geometrically: to find the area of a triangle, and to find the volume of a pyramid (or the area of a parallelogram and the volume of a parallelepiped). Last time we looked at what a determinant is, using some older questions; here we’ll first look at another old question that dealt specifically with volume, and then, in the recent question, we’ll see how the volume and area formulas are related. This will provide a second proof of the volume formula.
How determinants yield volume
This question, from 2002, is not directly about the volume of a parallelepiped, but comes very close by discussing a tetrahedron (triangular pyramid). I’ll point out the relationship as we work through this.
Volume of a Tetrahedron The volume of a tetrahedron is one-third the distance from a vertex to the opposite face, times the area of that face. Find a formula for the volume of a tetrahedron in terms of the coordinates of its vertices P, Q, R, and S. I'm not even sure where to begin. I think it may have something to do with cross product multiplication of vectors.
The assignment is to create a volume formula similar to the area formula (using a determinant) that we have seen for a triangle, given its vertices. From our perspective, we will be relating the algebraic definition of a \(3\times3\) determinant, from last time, to a volume.
Doctor Pete answered:
Thanks for writing to Dr Math. Don't despair - you do know where to begin, because you mentioned vectors. So I'll begin by setting up some vectors, which will be denoted by capital letters, in terms of their coordinates, which will be lowercase letters. Suppose you have vertices
P = (x1, y1, z1),
Q = (x2, y2, z2),
R = (x3, y3, z3),
S = (x4, y4, z4).
Furthermore, we will write
A = Q - P,
B = R - P,
C = S - P.
In essence, we translated vector P to the origin, and moved Q, R, S accordingly, to obtain A, B, and C; this will simplify our work.
Our vectors A, B, and C represent the sides of the tetrahedron (or of a parallelepiped) that meet at vertex P.
As an example, taking vertex P at the origin, and using vectors $$A=\left<2,-4,3\right>,B=\left<3,1,2\right>,C=\left<-3,2,1\right>,$$ we get this pyramid:
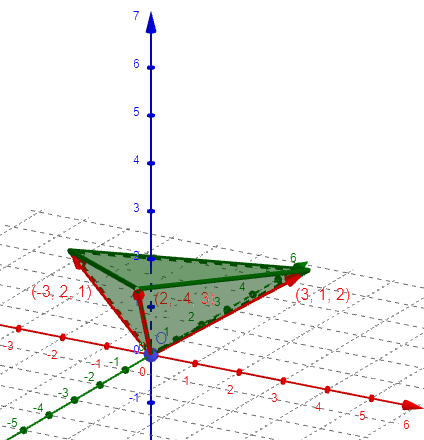
and this parallelepiped:
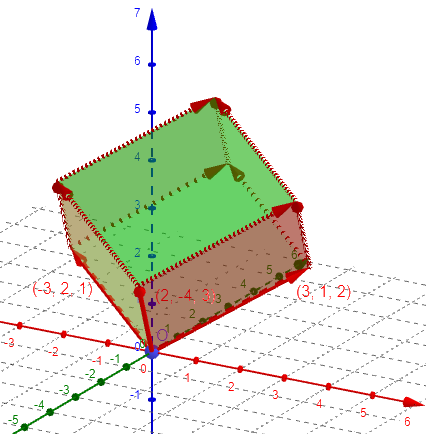
We’ll be using the scalar (dot) product and the vector (cross) product, which we’ve explored in past posts.
Now recall the dot product of two vectors
M = (m1, m2, m3), N = (n1, n2, n3)
satisfy the following properties:
[D1] M . N = m1*n1 + m2*n2 + m3*n3,
[D2] M . N = |M||N|Cos[t].
Here |M| signifies the magnitude (length) of M, and t is the angle between vectors M and N. As for the cross product, we have
| i j k |
[C1] M x N = | m1 m2 m3 |,
| n1 n2 n3 |
[C2] M x N = |M||N|Sin[t]*U,
where in [C1], i, j, k are the unit x-, y-, and z-vectors, and in [C2], U is the unit vector that is orthogonal to M and N and points in the direction as specified by the right-hand rule. (In particular, we have i x j = k, j x k = i, k x i = j.) A proof of these facts is given in all textbooks dealing with linear algebra.
He has shown, for each product, both an algebraic meaning (in terms of components) and a geometric meaning (in terms of lengths and areas), as explained in the links I provided above.
The second property about cross products is the main connection to the geometry of the problem, because geometrically it says that the cross product of two vectors is a third vector orthogonal to the other two, with magnitude equivalent to the area of the parallelogram defined by the two vectors. Perhaps a picture will show this:
N_______________
/| /
/ |h /
/ |_ /
/___|_|________/
0 M
In the above diagram we are looking at the plane containing the vectors M and N. The height h of the parallelogram is simply |N|Sin[t], where t is the angle M0N, the angle between M and N. Thus the area of the parallelogram is |M||N|Sin[t]. The vector M x N is pointing in a direction perpendicular to this plane (straight at you), by the right-hand rule.
This area will be the base of our parallelepiped.
The curious thing about the cross product, then, is that the area of the triangle determined by points M, N, and 0, is simply half the magnitude of the cross product, because the parallelogram consists of two congruent copies of triangle M0N. Thus, in the case of our vectors A, B, C, we may choose any two of these to show that the area of the triangular face determined by, say, vectors B and C, is simply
|B x C|/2.
The area of the parallelogram is just \(\text{Area }=|B\times C|\).
In our example, the area of the parallelogram formed by vectors B and C is the length of $$B\times C=\begin{vmatrix}\mathbf{i}&\mathbf{j}&\mathbf{k}\\3&1&2\\-3&2&1\end{vmatrix}=\left<-3,-9,9\right>,$$ namely $$|B\times C|=\sqrt{(-3)^3+(-9)^2+(9)^2}=\sqrt{171}$$
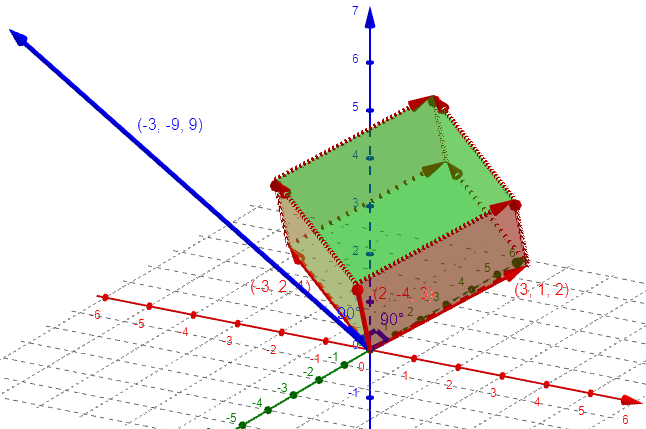
But wait - there's more. We observe that the vector B x C is parallel to the height from the vertex at A to the opposite face. If we draw another picture in the plane that contains the vectors B x C, A, and the length from A to the plane containing B and C, as follows,
B x C
|
| A
| /|
| /s|
| / |d
|s/ |
|/____|_____B___C
0 G
we see that B and C are now projected onto this plane and appear as a single line. The important thing to realize is that in this picture, vector A is in the same plane as B x C and the line segment AG. If we let s = angle 0AG, then we may write the distance d of AG as simply
d = |A|Cos[s].
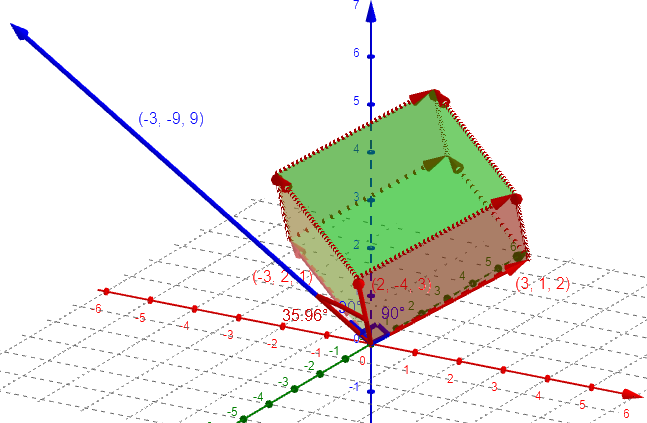
Here we see this angle between our \(A\) and \(B\times C\):
I can turn the image to show B and C approximately horizontal, the cross product vertical, and A at an angle:
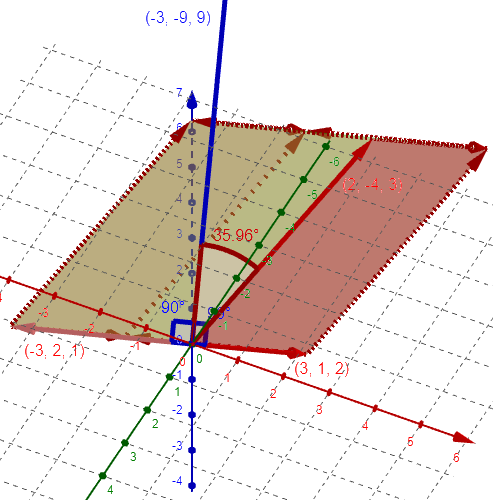
Since $$|A|=\sqrt{(2)^2+(-4)^2+(3)^2}=\sqrt{29},$$ and $$|B\times C|=\sqrt{(-3)^2+(-9)^2+(9)^2}=\sqrt{171},$$ and $$A\cdot(B\times C)=\left<2,-4,3\right>\cdot\left<-3,-9,9\right>=(2)(-3)+(-4)(-9)+(3)(9)=57,$$ the indicated angle is $$\arccos(\frac{57}{\sqrt{29}\sqrt{171}}=\arccos(0.8094)=35.96^\circ$$
But we don’t need to calculate the angle; we already have the volume:
Therefore, the volume of the tetrahedron is
V = (1/3)d|B x C|/2
= (1/6)|A||B x C|Cos[s].
But s is also the angle between A and B x C, and if we recall the formula [D2] for the dot product of two vectors, we find that
V = (1/6)|A . (B x C)|.
The product A . (B x C) is more commonly called the (scalar) triple product, because (with some slight details omitted) the symmetry of our argument reveals that
A . (B x C) = B . (C x A) = C . (A x B).
The volume of the parallelepiped is the same thing without the \(\frac{1}{6}\): \(\text{Volume }=A\cdot(B\times C)\).
Now we may write A . (B x C) in terms of the coordinates using the formulas [D1, C1]. We have
| i j k |
B x C = |x3-x1 y3-y1 z3-z1|,
|x4-x1 y4-y1 z4-z1|
and since A = (x2-x1, y2-y1, z2-z1), we immediately see that
|x2-x1, y2-y1, z2-z1|
A . (B x C) = |x3-x1, y3-y1, z3-z1|.
|x4-x1, y4-y1, z4-z1|
In terms of the vectors themselves, the volume of the parallelepiped determined by vectors \(A=\left<x_1,y_1,z_1\right>\), \(B=\left<x_2,y_2,z_2\right>\), and \(C=\left<x_3,y_3,z_3\right>\), would be $$\displaystyle\begin{vmatrix}x_1&y_1&z_1\\x_2&y_2&z_2\\x_3&y_3&z_3\end{vmatrix}$$
For our example, the volume is $$\begin{vmatrix}2&-4&3\\3&1&2\\-3&2&1\end{vmatrix}=\\(2)(1)(1)-(2)(2)(2)+(-4)(2)(-3)-(-4)(3)(1)+(3)(3)(2)-(3)(1)(-3)=\\2-8+24+12+18+9=57$$
This is just what we already calculated as that dot product!
Thus we have a formula for V in terms of the coordinates of P, Q, R, and S. But shouldn't this formula be symmetric in the coordinates? It is - it's just that it isn't obvious from looking at it. I leave it to you to show that the above determinant is equivalent to
|x1 y1 z1 1|
|x2 y2 z2 1|
|x3 y3 z3 1|
|x4 y4 z4 1| .
This is the usual form we use when we are given the coordinates of the vertices, rather than the components of the vectors. You can prove it is equal to the other by expanding each determinant as a sum of products, and seeing that they match.
Now let’s look at the recent question, which compares two of the determinant formulas:
Area, or volume? Both
The new question came from Rohit in early March:
I read somewhere that the determinant of a matrix of 3 × 3 represents the volume of the parallelepiped.
But when we try to find the area of a triangle using the determinant, then there is also a matrix of 3 × 3 order. So how is this formula telling the area, it should have told the volume?
Please clear my doubt.
This formula is one we discussed in Polygon Coordinates and Areas.
Doctor Rick answered:
Hi, Rohit.
Yes, the volume of a parallelepiped can be found using a determinant, and the area of a triangle can be found using a determinant. Obviously, the difference is in what determinant we use.
The volume of a parallelepiped with edges given by the vectors <x1, y1, z1>, <x2, y2, z2>, and <x3, y3, z3> — in other words, with a vertex at (0, 0, 0) and the three vertices adjacent to it at (x1, y1, z1), (x2, y2, z2), and (x3, y3, z3) — is the absolute value of the determinant:
| x1 y1 z1 | V = | x2 y2 z2 | | x3 y3 z3 |
This formula, which we saw above, uses three vectors, with three coordinates each, to describe a parallelepiped with one vertex at the origin.

Again, this volume, for our example, is $$\begin{vmatrix}2&-4&3\\3&1&2\\-3&2&1\end{vmatrix}=57$$
The triangle you’re talking about has vertices at (x1, y1), (x2, y2), and (x3, y3), in two dimensions. The determinant we use to find its area is
| x1 y1 1 | A = 1/2 | x2 y2 1 | | x3 y3 1 |
This uses three vertices, with two coordinates each.
For example, for this triangle,
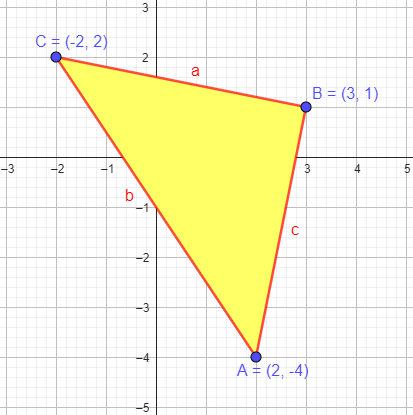
this formula gives $$\frac{1}{2}\begin{vmatrix}2&-4&1\\3&1&1\\-2&2&1\end{vmatrix}=\\\frac{(2)(1)(1)-(2)(1)(2)+(-4)(1)(-2)-(-4)(3)(1)+(1)(3)(2)-(1)(1)(-2)}{2}=\\\frac{2-4+8+12+6+2}{2}=\frac{26}{2}=13$$ (To check, it turns out to be a right triangle with legs \(\sqrt{26}\), whose area is … 13.)
So we have two different formulas, both using determinants, which give a volume and an area respectively.
It just isn’t the same thing; it isn’t at all surprising that it calculates a different quantity. In fact, the determinant here cannot give a volume. If the coordinates have the dimension of length (say, each is in meters), then the determinant (with terms of the form xiyj) will have units of meters squared, not meters cubed.
Recall from last week that a \(3\times3\) determinant is a sum of terms, each of which is a product of a number from each row and each column, so each term in this case is \(x_i\cdot y_j\cdot1\), which is in square units.
Checking dimensions can help distinguish formulas.
Are the two formulas related?
Now comes the fun part:
But can we find a connection between the two formulas? Yes, we can! It isn’t easy — I have never thought about it this way before — but it can be done.
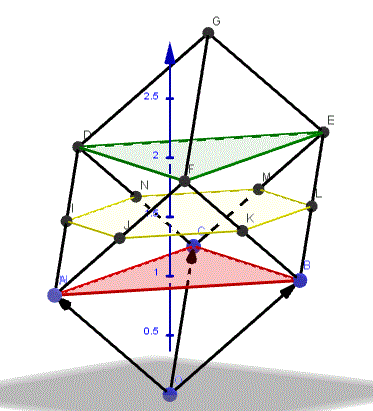
Let’s put the triangle in the plane z = 1 of three-dimensional space, with the vertices at (x1, y1, 1), (x2, y2, 1), and (x3, y3, 1). (Here, 1, being a z coordinate, is a length, like the x’s and y’s.) Now regard those three vertices as the three vertices of a parallelepiped with fourth vertex (0, 0, 0). The volume of this parallelepiped is given by the formula above. Here is a figure.
The triangle we are starting with, ABC, is in red; the black lines are the edges of the parallelepiped, which is determined by the three vectors \(OA=\left<x_1,y_1,1\right>\), \(OB=\left<x_2,y_2,1\right>\), and \(OC=\left<x_3,y_3,1\right>\), so the volume formula gives $$\begin{vmatrix}x_1&y_1&1\\x_2&y_2&1\\x_3&y_3&1\end{vmatrix}$$
The two horizontal triangles, red and green, are congruent; the area of each is the area A calculated above.
They dissect the parallelepiped into two pyramids, each with volume 1/3 Ah, where the height h is 1, and a prismatoid whose volume is given by
Vp = 1/6 (A1 + 4M + A2)
where A1 = A2 = A, the area of the triangle, and M is the area of the hexagon shown in yellow, midway between the two triangular sections.
The pyramids at the top and bottom, with red and green triangular bases, each have area \(\frac{1}{3}A\). Each side of the hexagon is the midline of a triangle, and so is half the length of a side of the triangle; for example, side JK is a midline of triangle ABF, so its length is half that of segment AB.
Here we see the red and green triangles (relabeled as \(ABC\) and \(A’B’C’\)), and you can see that the solid red triangle \(A”B”O\) is similar to \(ABC\), with sides half as long. Repeating this observation, the hexagon can be divided into six triangles, each of which is \(\frac{1}{4}\) the area of triangle \(ABC\):
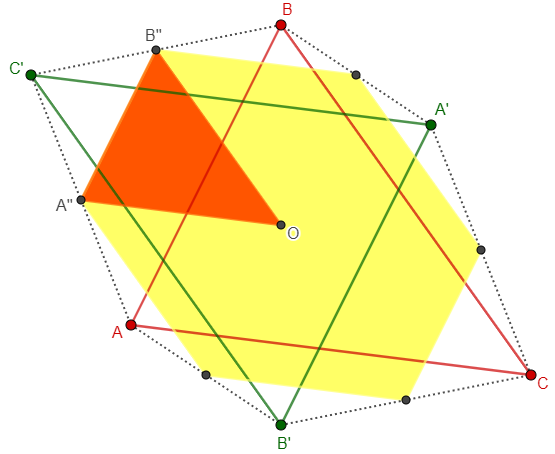
Therefore, \(M=6\left(\frac{1}{4}A\right)=\frac{3}{2}A\). We can put this into the formula for the volume of the prismatoid, and add on the two pyramids, to find the total volume V:
It can be shown that M = 3/2 A, so that the total area of the parallelepiped is
V = 1/3 A + 1/6 (A + 4(3/2 A) + A) + 1/3 A = 2A
So
| x1 y1 1 | V = | x2 y2 1 | | x3 y3 1 |This is just the determinant in the formula above for the volume of the parallelepiped with vertices at (0, 0, 0), (x1, y1, 1), (x2, y2, 1), and (x3, y3, 1).
If you missed it, he has shown that the volume of the parallelepiped is 2 units of length times the area of the triangle (in square units), so we just have to multiply the formula for the area by 2, which cancels out the \(\frac{1}{2}\):
$$A=\frac{1}{2}\begin{vmatrix}x_1&y_1&1\\x_2&y_2&1\\x_3&y_3&1\end{vmatrix}$$
$$V=\frac{1}{3}A+\frac{1}{6}\left(A+4\left(\frac{3}{2}A\right)+A\right)+\frac{1}{3}A=2A=\begin{vmatrix}x_1&y_1&1\\x_2&y_2&1\\x_3&y_3&1\end{vmatrix}$$
But this is the same result we get when we apply
$$V=\displaystyle\begin{vmatrix}x_1&y_1&z_1\\x_2&y_2&z_2\\x_3&y_3&z_3\end{vmatrix}$$
to our three vectors \(\left<x_1,y_1,1\right>\), \(\left<x_2,y_2,1\right>\),\(\left<x_3,y_3,1\right>\). So we’ve derived the matrix formula for this particular parallelepiped from the formula for the area of a triangle.
There are much better ways to prove the parallelepiped volume formula than this! However, it does show that the two formulas you asked about are consistent.
So, if we didn’t have a proof for the volume determinant, we could obtain it by way of the area determinant.
Of course, this is a special parallelepiped, with z-components of the three vertices all equal to 1, so it doesn’t directly prove the formula for any three vectors. With some work, we could generalize it. But the goal here was primarily to show the compatibility of the two determinant formulas.