Continuing our look at the Fibonacci sequence, we’ll extend the idea to “generalized Fibonacci sequences” (with different starting numbers), and see that the ratio of consecutive terms is the same in general as in the usual special case. Then we’ll look at the sum of terms of both the special and general sequence, turning it into a series. This turns out to be as simple as you could imagine!
Generalized Fibonacci sequences
Recall that the Fibonacci sequence is defined by specifying the first two terms as \(F_1=1\) and \(F_2=1\), together with the recursion formula \(F_{n+1}=F_n+F_{n-1}\). We have seen how to use this definition in various kinds of proofs, and also how to find an explicit formula for the nth term, and that the ratio between successive terms approaches the golden ratio, \(\phi\), in the limit.
Similar questions can be raised about any sequence that has the same recursion as the Fibonacci sequence, but starts with a different pair of numbers. That is the subject of a question from 2002:
Generalised 'Fibonacci' Series and Phi I have searched but I can't find an answer to this. I have shown with a spreadsheet that a Fibonacci-style series that starts with any two numbers at all, and adds successive items, produces a ratio of successive items that converges to phi in about the same number of terms as for the 1 1 2 3 5 etc. basic Fibonacci series. I can't find reference to this - maybe I don't know how to look - surely this is well known? Is it - and is it provable?
None of these series converges to \(\phi\) in a finite number of terms, but presumably Stuart means that it converges to about the same precision in about the same number of steps. Here is an example of a spreadsheet showing this (which is very easy to make):
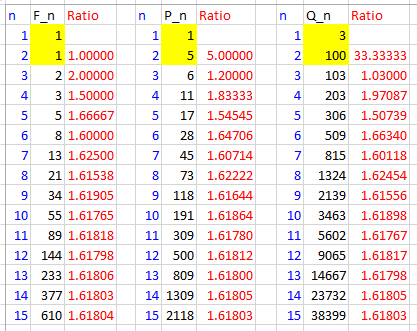
The first column is Fibonacci proper, starting with 1, 1; these are the numbers we call the Fibonacci numbers. The second starts with 1, 5 (which we’ll be seeing later), and the third, just to be very different, starts with 3, 100. The ratios in each case rapidly converge toward 1.618034…, which is \(\phi\).
Doctor Floor answered:
Hi, Stuart, Thanks for your question. To prove your conjecture we will delve into formulas of generalized Fibonacci sequences (sequences satisfying X(n) = X(n-1) + X(n-2) ). Let's first investigate two very special members of the family of generalized Fibonacci sequences, those of the form X(1)=g=g^1, X(2)=g^2, X(3)=g^3, ..., X(n)=g^n [g nonzero]
In other words, is it possible for a sequence with this recursion to also be a geometric sequence? That’s not the first question I’d think to ask about generalized Fibonacci sequences; but it turns out to be interesting:
Since X(n)=X(n-1)+X(n-2), we must have: g^n = g^(n-1) + g(n-2) g^n - g^(n-1) - g(n-2) = 0 g^(n-2) * (g^2 - g - 1) = 0 g^2 - g - 1 = 0 [we can divide by g^(n-2) because g is nonzero] So g must be one of the roots of g^2 - g - 1 = 0, so it must be one of the following numbers: Phi = (1+SQRT(5))/2 (the Golden Ratio) 1-Phi = (1-SQRT(5))/2
Only these two numbers can work as the common ratio. We could actually start the sequence with any number we like (including 1), so there are many such geometric “Fibonacci” sequences (which would be multiples of these); but taking the sequences as \(A_n = \phi^n\) and \(B_n = (1-\phi)^n\) will keep the formulas simple.
So we have two very special generalized Fibonacci sequences: Phi^1, Phi^2, Phi^3, ..., Phi^n, ... (1-Phi)^1, (1-Phi)^2, ..., (1-Phi)^n, ... I leave it for you to check that, when you have two generalized Fibonacci sequences A(n) and B(n), and two numbers a and b, then a*A(n) + b*B(n) is a generalized Fibonacci sequence.
Let’s do that: If \(A_n\) and \(B_n\) satisfy the recursions \(A_n=A_{n-1}+A_{n-2}\) and \(B_n=B_{n-1}+B_{n-2}\), and \(C_n=aA_n+bB_n\), then $$C_{n-1}+C_{n-2} = (aA_{n-1}+bB_{n-1})+(aA_{n-2}+bB_{n-2})\\ = a(A_{n-1}+A_{n-2})+b(B_{n-1}+B_{n-2}) = aA_n+bB_n = C_n.$$
So any linear combination of any two generalized Fibonacci sequences is also a generalized Fibonacci sequence.
In fact, all generalized Fibonacci sequences can be calculated in this way from Phi^n and (1-Phi)^n. This can be seen from the fact that any two initial terms can be created by some a and b from two (independent) pairs of initial terms from A(n) and B(n), and thus also from Phi^n and (1-Phi)^n. So each generalized Fibonacci sequence can be written as X(n) = a*Phi^n + b*(1-Phi)^n.
For example, suppose (as in my second column above) that we want the first two terms of our sequence to be \(X_1=1\) and \(X_2=5\). Then we want to find a and b such that $$a\phi+b(1-\phi)=1\\a\phi^2+b(1-\phi)^2=5.$$ These equations simplify (using the fact that \(\phi^2=\phi+1\)) to $$(a-b)\phi+b=1\\(a-b)\phi+(a+2b)=5.$$ Subtracting to eliminate the first term, we find that $$a+b=4.$$ (We could have obtained the same result trivially by using \(X_0=4\)!)
Replacing \(b\) with \(4-a\) in the first equation, we get $$(2a-4)\phi+(4-a)=1\\ (2\phi-1)a+(4-4\phi)=1\\ a=\frac{4\phi-3}{2\phi-1}=\frac{2\sqrt{5}-1}{\sqrt{5}}\\ b=4-\frac{2\sqrt{5}-1}{\sqrt{5}}=\frac{2\sqrt{5}+1}{\sqrt{5}}.$$ So our sequence is $$X_n=\frac{2\sqrt{5}-1}{\sqrt{5}}\phi^n+\frac{2\sqrt{5}+1}{\sqrt{5}}(1-\phi)^n.$$ This can be done for any initial pair of terms.
Now your statement follows for all sequences for which a<>0, when we realize that |1-Phi|<1, so that (1-Phi)^n --> 0 for n --> infinity. So we see that there are exceptions: sequences b*(1-Phi)^n.
This is the same reasoning we used before for the limit of the Fibonacci sequence proper, at the end of The Golden Ratio and Fibonacci. And if it turns out that \(a=0\), then the limit is zero rather than \(\phi\).
We’ll be seeing more on the generalized Fibonacci sequence below!
Summing the Fibonacci series
It is common to mistakenly use the term “series” (which refers to a sum) in place of the word “sequence” (which is what the Fibonacci numbers are, an ordered list). We even see that in the original title for the question above, which was taken from the question. But this time we’re really going to talk about the Fibonacci series: What do you get when you add up the Fibonacci numbers?
This question is from 2000:
Sum of Fibonacci Series Is there any formula for the sum of the first n numbers in the Fibonacci sequence? I've been looking for one without success. I did find a quartic equation that worked for the first few (five or six), but it got progressively more inaccurate. I have also tried plotting them against the respective terms of the Fibonacci sequence, which almost gave a straight line, but it was not quite close enough.
Edward has been trying to guess at a formula; I tried fitting the sequence to a quartic polynomial using Excel, which did fairly well for the first 15 terms as in my table above, but not exact:
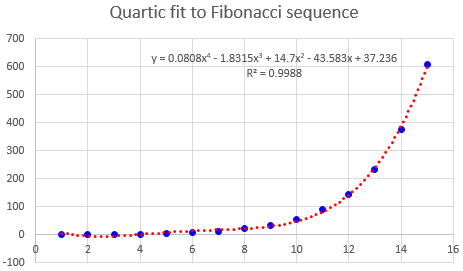
If I plotted more Fibonacci numbers with the same polynomial, they would rapidly diverge – because the Fibonacci sequence is closely related to exponential functions (geometric sequence) as we’ve already seen, and therefore grows faster than any polynomial.
Doctor Mitteldorf answered first, with a hint and a challenge:
Dear Edward,
Believe it or not, the Fibonacci series is the sum of two geometric series, each one of which separately is not even an integer. Given the formula, it's not too hard to prove that it works (use proof by induction). But where does the formula come from?
The formula involves the square root of 5, which I write as sqrt[5]. The nth Fibonacci is:
a*x^n + (1-a)*y^n
where a = (3+sqrt[5])/(5+sqrt[5])
x = (1+sqrt[5])/2
y = (1-sqrt[5])/2
We’ve already seen such a formula both “discovered” and proved; this version is different because, for some reason, he chose to start with 1 and 2 rather than 1 and 1. (You might like to try obtaining the formula using the method above for the generalized sequence!)
So my challenges to you are: first, to prove that the formula works, and second, to derive the equation you want for the sum of the first n terms, using the formula for the sum of a geometric series.
We don’t need to prove the formula; and I’ll leave you to find the formula for the sum, based either on Doctor Mitteldorf’s version or Binet’s. As a reminder, here is the formula for the sum of a finite geometric series with \(a_0=a\) and common ratio \(r\):
$$\sum_{k=0}^n ar^k = a+ar+ar^2+ar^3+\cdots+ar^n = \frac{a(r^{n+1}-1)}{r-1}.$$
For example, $$\sum_{k=0}^3 3\cdot 2^k = 3+6+12+24 = \frac{3(2^4-1)}{2-1} = 45.$$
Then Doctor Floor, writing at the same time, gave a fuller answer:
Hi, Edward,
Thanks for writing.
We know that the nth Fibonacci number
F(n) = (PHI^n - (1 - PHI)^n) / sqrt[5]
where PHI = (1+sqrt[5])/2 = 'Golden ratio'
This, of course, is the usual Binet formula for the sequence starting with 1, 1, which is the difference of two geometric series.
I will use the value of F(0) in my sum of the first n Fibonacci numbers. That doesn't matter because F(0) = 0.
So we can derive the following:
SUM{i = 0 to n} F(n)
= SUM{i = 0 to n} (PHI^i - (1 - PHI)^i) / sqrt5
= (1/sqrt5)*{[SUM{i = 0 to n} PHI^i] - [SUM{j = 0 to n} (1-PHI)^j]}
Here we will be applying the formula I stated above, with \(a=1\) for each series, and with common ratios \(\phi\) and \((1-\phi)\) respectively:
$$\sum_{k=0}^n \phi^k = \frac{\phi^{n+1}-1}{\phi-1}$$
$$\sum_{k=0}^n (1-\phi)^k = \frac{(1-\phi)^{n+1}-1}{(1-\phi)-1} = \frac{(1-\phi)^{n+1}-1}{-\phi}$$
Using the formula for a geometric series we know:
SUM{i = 0 to n} PHI^i = (PHI^(n+1)-1)/(PHI - 1)
and
SUM{j = 0 to n} (1-PHI)^j = ((1-PHI)^(n+1) - 1)/-PHI
so we conclude:
(1/sqrt[5])*{[SUM{i = 0 to n} PHI^i] - [SUM{j = 0 to n} (1-PHI)^j]}
( PHI^(n+1) - 1 (1-PHI)^(n+1) - 1 ) 1
= ( ------------- + ----------------- )* -------
( PHI-1 PHI ) sqrt[5]
PHI^(n+2) - PHI - (1-PHI)^(n+2) - PHI + 1
= ----------------------------------------- [use PHI*(PHI-1) = 1]
sqrt5*PHI*(PHI-1)
PHI^(n+2) - (1-PHI)^(n+2) 1 - 2*PHI
= ------------------------- + ---------
sqrt[5] sqrt[5]
= F(n+2) - 1
After a bit of fraction work and recognizing the Binet formula coming back to us, the result is amazingly simple – not a polynomial in n, but one less than a subsequent term in the sequence.
We see that there comes a very simple formula
{F(0) +} F(1) + F(2) + ... + F(n) = F(n+2) - 1
_^^^^^^^^_
not needed
Now that we found the formula, it seems that you can prove it more easily by mathematical induction. Try it!
Series sum by induction
Let’s do it! We want to prove that for any positive integer n, the sum of the first n terms of the Fibonacci sequence is \(F_{n+2}-1\). That is, $$\sum_{i=1}^n F_i = F_{n+2}-1$$
Base case: We’ll use weak recursion (not strong as we have often used with Fibonacci), and only need one case: $$\sum_{i=1}^1 F_i = F_1 = 1\\ F_{1+2}-1=F_3-1=2-1=1$$
Inductive hypothesis: Suppose that the sum of the first \(k\) terms is \(F_{k+2}-1\): $$\sum_{i=1}^k F_i = F_{k+2}-1$$ We want to show that the sum of the first \((k+1)\) terms is \(F_{(k+1)+2}-1 = F_{k+3}-1\): $$\sum_{i=1}^{k+1} F_i = F_{k+3}-1$$
Induction: The sum of the first \((k+1)\) terms is the sum of the first \(k\) terms plus the \((k+1)\)st:
$$\sum_{i=1}^{k+1} F_i = \sum_{i=1}^k F_i+F_{k+1}=(F_{k+2}-1)+F_{k+1}=(F_{k+2}+F_{k+1})-1=F_{k+3}-1$$
by the recursion. That was easy!
Summing the generalized Fibonacci series
Our final question (from 2003) combines these ideas, summing a generalized series.
Sum of Sequence: a, b, a+b, a+2b, 2a+3b... Is there a formula to find the sum of the first n terms of the sequence a, b, a+b, a+2b, 2a+3b... ? If I know a and b, and how many terms, is there a way to find the sum? Question: Find the sum of the first 30 terms of the sequence: 1, 5, 6, 11, 17, 28... if the 30th term is 2888956 and the 31st term is 4674429. Thanks.
Do you recognize that, though the name wasn’t used, this is about the generalized Fibonacci sequence, starting with any two numbers a and b? Will it be as simple as for the standard sequence?
Doctor Jacques answered:
Hi Daniel, Although your sequence is not the Fibonacci sequence, it looks a lot like it and the formula is the same: a[n+2] = a[n+1] + a[n] We can also write it as: a[n] = a[n+2] - a[n+1] Let us write some terms, starting at the end: a[29] = a[31] - a[30] a[28] = a[30] - a[29] a[27] = a[29] - a[28] ...... a[2] = a[4] - a[3] a[1] = a[3] - a[2] We notice that, on the right side, the first term of each equation (starting at the second) also appears with a minus sign in the previous equation. This means that, if we add together all the equations, a lot of terms will cancel each other.
This is a less formal way to do the same thing we did in the recursion earlier. Just imagine crossing off both a[30]’s, then both a[29]’s, and so on down to the a[3]’s. What’s left?
On the left-hand side, we will have a[1] + ... + a[29] - this is almost what we are looking for. On the right-hand side: The first (a[31]) will remain there All the terms from a[30] down to a[3] will cancel out The last term (-a[2]) will remain. To summarize, after all simplifications, we get: a[1] + ... + a[29] = a[31] - a[2] As we know a[30], a[31], and, of course, a[2], you should be able to complete the calculation.
Turning this into an explicit formula for the sum in the general case (since n in our example is 30), $$A_1+A_2+\dots+A_{n-1} = A_{n+1}-A_2$$ so that, add \(A_n\) to both sides, $$A_1+A_2+\dots+A_{n-1}+A_n = A_n+A_{n+1}-A_2 = A_{n+2}-A_2$$
This is exactly equivalent to the standard case above.
For the particular numbers we were given, \(A_1=1\), \(A_2=5\), and \(A_{32} =A_{30}+A_{31}\) \( =2,888,956+4,674,429\) \(=7,563,385\), so the sum is \(A_{32}-A_2=7,563,385-5\) \(=7,563,380\).
While we’re here, let’s check whether the numbers we were given are correct. Remember the specific sequence we worked out earlier? That was for \(X_1=1\) and \(X_2=5\), and we found that $$X_n=\frac{2\sqrt{5}-1}{\sqrt{5}}\phi^n+\frac{2\sqrt{5}+1}{\sqrt{5}}(1-\phi)^n.$$ Therefore, $$X_{30}=\frac{2\sqrt{5}-1}{\sqrt{5}}\phi^{30}+\frac{2\sqrt{5}+1}{\sqrt{5}}(1-\phi)^{30} = 2888955.9999987+0.0000013=2888956m$$ which is what we were told it was. The author of the problem either used the formula or, more likely, used a spreadsheet to make the sequence. They didn’t just toss out a fake number figuring no one would ever check.

Pingback: Fibonacci Word Problems I: Basic – The Math Doctors